Kolokwium nr 1
Grupa 1 WILiŚ
RZĄD A 04-11-2004
Zadanie 1. Obliczyć granice następujących ciągów:
a). ![]()
, b). 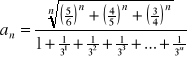
, c). ![]()
.
Zadanie 2. Wyznaczyć wartość parametrów ![]()
tak, aby funkcja była ciągła:
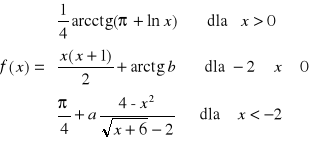
.
Zadanie 3. Wyznaczyć funkcję odwrotną ![]()
, dziedzinę i przeciwdziedzinę ![]()
gdy:
a). ![]()
, b). ![]()
.
Zadanie 4. Korzystając z reguły de L'Hospitala obliczyć podane granice:
a). ![]()
, b). ![]()
.
Zadanie 5. Obliczyć pochodne podanych funkcji:
a). ![]()
, b). ![]()
.
T: Podać definicję ciągu ograniczonego. Sformułować jedno z twierdzeń dotyczących zbieżności ciągów ograniczonych i podać przykład ilustrujący wybrane twierdzenie.
Kolokwium nr 1
Grupa 1 WILiŚ
RZĄD B 04-11-2004
Zadanie 1. Obliczyć granice następujących ciągów:
a). 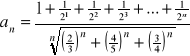
, b). ![]()
, c). 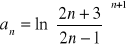
.
Zadanie 2. Wyznaczyć wartość parametrów ![]()
tak, aby funkcja była ciągła:
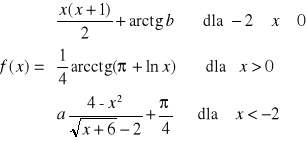
.
Zadanie 3. Wyznaczyć funkcję odwrotną ![]()
, dziedzinę i przeciwdziedzinę ![]()
gdy:
a). ![]()
, b). ![]()
.
Zadanie 4. Korzystając z reguły de L'Hospitala obliczyć podane granice:
a). ![]()
, b). ![]()
.
Zadanie 5. Obliczyć pochodne podanych funkcji:
a). ![]()
, b). ![]()
.
T: Podać definicję ciągu monotonicznego. Sformułować twierdzenie o ciągu monotonicznym i ograniczonym. Zbadać monotoniczność ciągu ![]()
.
Kolokwium nr 1
Grupa 5 WBWiIŚ
13-11-2003
Zadanie 1 Obliczyć granice ciągów o wyrazach ogólnych:
a). ![]()
b). 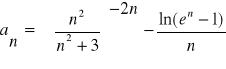
.
Zadanie 2 Wyznaczyć przedziały monotoniczności i ekstrema funkcji ![]()
.
Zadanie 3 Zbadać ciągłość funkcji ![]()
. Jeśli istnieją punkty nieciągłości, określić ich rodzaj:
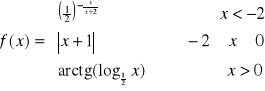
.
Zadanie 4 Wyznaczyć przedziały wypukłości i wklęsłości, oraz punkty przegięcia funkcji ![]()
.
Zadanie 5 Napisać równanie stycznej do krzywej 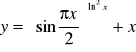
w punkcie ![]()
T1. Podać twierdzenie o trzech ciągach.
T2. Definicja Heinego granicy właściwej funkcji w punkcie.
T3. Definicja pochodnej funkcji.
2002/2003
RZĄD A
Obliczyć granice ciągów o wyrazach ogólnych:
a). ![]()
b). 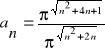
Wyznaczyć dziedzinę funkcji:
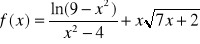
Wyznaczyć przedziały monotoniczności i ekstrema funkcji
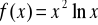
.Napisać równanie stycznej do krzywej
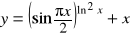
.Wyznaczyć pochodną funkcji
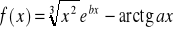
, gdy
![]()
oraz ![]()
.
Podać definicję Heinego granicy funkcji w punkcie i na podstawie tej definicji pokazać, że

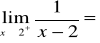
.
2001/2002
GRUPA 1
Zadanie 1. Obliczyć granicę :
a). ciągu 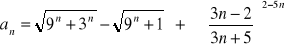
b). funkcji (korzystając z reguły de L'Hospitala) ![]()
Zadanie 2. Obliczyć z definicji pochodną funkcji ![]()
Zadanie 3. Obliczyć ![]()
jeżeli ![]()
.
Zadanie 4. Wyznaczyć funkcję odwrotną do danej oraz jej dziedzinę
![]()
Zadanie 5. Wyznaczyć wartość parametru ![]()
dla którego podana funkcja jest ciągła
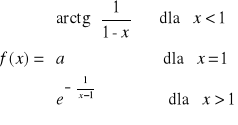
Zadanie 6. Podać definicję ciągu ograniczonego, oraz jedno z twierdzeń dotyczących takich
ciągów. Podać odpowiedni przykład.
2001/2002
GRUPA 2
Zadanie 1. W jakim punkcie (punktach) styczna do krzywej ![]()
tworzy z osią OX kąt ![]()
?
Zadanie 2. Obliczyć ![]()
jeżeli ![]()
Zadanie 3. Obliczyć :
a). granicę funkcji (korzystając z reguły de L'Hospitala) ![]()
b). granicę ciągu: ![]()
Zadanie 4. Wyznaczyć wartość parametru ![]()
dla którego podana funkcja jest ciągła:
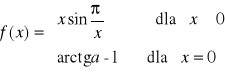
Zadanie 5. Wyznaczyć funkcję odwrotną do danej, oraz jej dziedzinę
![]()
.
Zadanie 6. Sformułować twierdzenie Rolle'a i podać jego interpretację geometryczną.
Wyszukiwarka