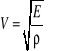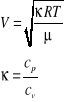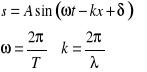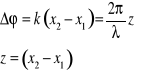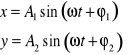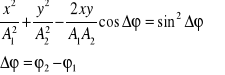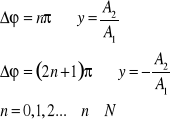Ćwiczenie nr 21

Wyznaczanie prędkości rozchodzenia się fal dźwiękowych metodą składania drgań wzajemnie prostopadłych

1. Cel ćwiczenia

Wyznaczenie prędkości dźwięku w powietrzu z przesunięcia fazy pomiędzy mikrofonem a głośnikiem. Analiza krzywych Lissajous.

2. Wprowadzenie

Fala to zaburzenie pola fizycznego rozchodzące się ze skończoną prędkością i przenoszące energię ,ale nie masę. Zaburzenie rozchodzące się w ośrodku sprężystym przenoszące energię przez drgające cząsteczki ośrodka bez zmiany ich średniego położenia nazywamy falą akustyczną. Dźwięki z zakresu częstotliwości fal od około 16 Hz do 20 kHz to dźwięki słyszalne. Dźwięki poniżej 16 Hz to infradźwięki, a powyżej 20 kHz to ultradźwięki. Ze względu na kierunek drgań cząsteczek ośrodka fale dzielimy na podłużne i poprzeczne. W fali podłużnej kierunek drgań cząsteczek jest równoległy do kierunku propagacji fali, a w fali poprzecznej jest on prostopadły. Prędkość rozchodzenia się fali zależy tylko od właściwości ośrodka, w którym się rozchodzi. Fale poprzeczne rozchodzą się w ciałach stałych i na swobodnej powierzchni cieczy. Fale podłużne związane z odkształceniem objętościowym ośrodka rozchodzą się w każdym środowisku.

Źródłami fal-są ciała powodujące zaburzenia ośrodka. Prędkość dźwięku jest to prędkość rozchodzenia się fal dźwiękowych w danym ośrodku sprężystym. Prędkość zależy od wielu czynników np. naprężeń i gęstości w przypadku ciał stałych, temperatury w przypadku gazów. Prędkość fali podłużnej w ciele stałym można wyliczyć ze wzoru

(21.1)

gdzie:

E - moduł Younga

Ρ- gęstość ośrodka

W gazach przyjmując ,że rozchodzenie się fali jest procesem adiabatycznym otrzymujemy:

	(21.2)
		(21.3)

gdzie:

κ - wykładnik adiabaty,

R - uniwersalna stała gazowa,

μ - masa cząsteczkowa gazu,

T - temperatura w skali bezwzględnej.

Równanie fali akustycznej rozchodzącej się wzdłuż osi x zapisujemy następująco:

	(21.4)
		(21.5)

gdzie:

A - amplituda drgań, czyli największe wychylenie cząstki ze stanu równowagi,

ω - częstość kołowa drgań,

δ - faza początkowa drgań,

k - liczba falowa.

Długość fali λ wynosi:

(21.6)

gdzie:

V - prędkość dźwięku,

T - okres fali,

f - częstotliwość.

Fala dźwiękowa w danym ośrodku rozchodzi się ze skończoną prędkością V. Dlatego drgania cząsteczek ośrodka, w którym rozchodzi się fala są przesunięte w fazie. Różnicę faz drgań cząsteczek ośrodka w miejscu źródła fali i punkcie odległym o z wyznaczamy ze wzoru:

	(21.7)
		(21.8)

gdzie:

x₂ i x₁ - 2 punkty fali rozchodzącej się wzdłuż osi x.

Dla z = λ i całkowitej wielokrotności tej wielkości otrzymujemy drgania zgodne w fazie.

Długość fali akustycznej można wyznaczyć przez pomiar odległości miedzy dwoma punktami fali i z różnicy faz pomiędzy nimi. Różnicę faz możemy wyznaczyć metodą złożenia drgań wzajemnie prostopadłych. Po nałożeniu się takich drgań o jednakowych częstotliwościach, krzywa opisująca drganie wypadkowe zależy od różnicy faz drgań pierwotnych.

Schemat zestawu pomiarowego przestawiono na rysunku 21.2.Głosnik wraz z mikrofonem ustawiono naprzeciwko siebie na ławie pomiarowej. Sygnał z generatora akustycznego przykładany jest do głośnika i jednocześnie równolegle do płytek odchylania pionowego oscyloskopu. Fala dźwiękowa z głośnika dociera do mikrofonu wytwarzając w nim sygnał elektryczny przykładany następnie do płytek odchylających poziomo oscyloskopu. Głośnik jest jednocześnie źródłem fali i jednym z punktów pomiarowych. Mikrofon można przesuwać wzdłuż ławy i określać jego położenie na podziałce. Przyłożone sygnały elektryczne do płytek odchylania x i y oscyloskopu powodują, że strumień elektronów lampy oscyloskopu będzie uczestniczył w dwóch, wzajemnie prostopadłych drganiach. Jest to przypadek złożenia dwóch ruchów harmonicznych o jednakowych częstotliwościach w kierunkach wzajemnie prostopadłych. W wyniku takiego złożenia otrzymujemy wypadkowe drganie, które też jest drganiem harmonicznym, a którego torem jest elipsa. Równanie elipsy zależy od różnicy faz drgań składowych. Jeżeli drgania wzdłuż osi x i y zapiszemy następująco:

	(21.9)
		(21.10)

gdzie:

A₁, A₂ - amplitudy drgań,

ω - częstość drgań,

φ_1, φ₂ - początkowe fazy drgań.

Ogólne równanie elipsy dla drgań wzajemnie prostopadłych o jednakowych częstościach zapisujemy następująco:

	(21.11)
		(21.12)

Δφ oznacza różnicę faz drgań składowych. W zależności od różnicy faz drgania odbywają się wzdłuż elipsy, okręgu lub prostej(rysunek 3.) Jeśli różnica faz Δφ jest równa nieparzystej wielokrotności π/2 torem drgań jest okrąg .Jeśli Δφ=0, π,2π… drgania odbywają się wzdłuż prostej:

	(21.13)
		(21.14)
		(21.15)

Rys. 21.1 Wykresy toru drgań otrzymanych w wyniku złożenia 2 drgań w kierunkach
wzajemnie prostopadłych w zależności od różnicy faz Δφ.

Krzywe pokazane na rysunku 21.1. są przykładem tzw. krzywych Lissajous. Najmniejsza odległość z = x₂ - x₁ ,dla której otrzymujemy drgania zgodne w fazie, jest równa długości fali dźwiękowej w powietrzu λ. Stąd możemy wyznaczyć prędkość dźwięku:

(21.16)

gdzie f oznacza częstotliwość fali.

3. Opis stanowiska laboratoryjnego

Rys. 21.2 Schemat aparatury do pomiaru prędkości dźwięku metodą pomiaru różnicy faz

Schemat zestawu pomiarowego przestawiono na rysunku 21.2. Składa się on z generatora akustycznego, oscyloskopu, ławy pomiarowej, na której umieszczono naprzeciwko siebie głośnik i mikrofon, kable połączeniowe, przymiar liniowy. Zasadę pomiaru opisano szczegółowiej w punkcie 2).

4. Program ćwiczenia

1. Sprawdzić połączenia układu pomiarowego według schematu przedstawionego na rysunku1.Włączyć generator akustyczny i oscyloskop.

2. Nastawić na generatorze częstotliwość f = 1000 Hz.

3. Przesuwać mikrofon wzdłuż ławy pomiarowej aż na ekranie oscyloskopu pojawi się linia prosta. Zanotować położenie mikrofonu x₁ i jego niepewność pomiarową Δx₁.

4. Przesuwać dalej mikrofon i notować jego położenie x_n, gdy na ekranie oscyloskopu pojawią się kolejne proste, o takim samym nachyleniu(współczynniku kierunkowym).

5. Zwiększyć częstotliwość generatora i powtórzyć czynności z punktu 2-5 dla 6 innych częstotliwości.

6. Ustalić i zanotować niepewności pomiarowe Δf, Δx_n.

7. Wyniki umieścić w tabeli 21.1.

Tabela 21.1

Δf= Δ(x₂ - x₁)=

lp.	f[kHz]	x1[m]	x2[m]	z=(x2-x1) [m]	Δ(x2-x1) [m]	λ[m]	v[m/s]

5. Sprawozdanie

1. Oblicz prędkość dźwięku w temperaturze otoczenia dla wszystkich częstotliwości f.

2. Oblicz niepewności względne pomiaru prędkości dźwięku dla stosowanych częstotliwości ze wzoru:

(21.17)

oraz niepewności bezwzględne. Wartości niepewności bezwzględnej Δv otrzymujemy mnożąc wyliczoną maksymalną niepewność względną pomiaru Δv/v przez otrzymaną doświadczalnie wartość prędkości dźwięku c dla danej częstotliwości f. Czynność tą powtarzamy dla wszystkich częstotliwości f.

3. Korzystając z programu „regresja liniowa” lub z arkusza kalkulacyjnego Excel sprawdzić liniowość wykresu Δ(x₂-x₁) = f(l/f). oraz zapisać wyliczone przez program współczynniki regresji a, b równania prostej y = ax + b oraz ich odchylenia standardowe i współczynnik korelacji. Na podstawie otrzymanej wartości współczynnika kierunkowego prostej a obliczyć wartość v. i zapisać ją wraz z jednostką.

4. Wykonać wykres zależności Δ(x₂-x₁) od odwrotności częstotliwości generatora (1/f). Nanieść niepewności systematyczne. Sprawdzić czy punkty pomiarowe układają się wzdłuż prostej.

5. Narysować prostą przechodzącą przez największą ilość prostokątów niepewności pomiarowy. Wyznaczyć współczynnik nachylenia prostej.i na tej podstawie wyznaczyć wartość prędkości dźwięku v.

6. Przeprowadzić dyskusje wyników i niepewności pomiarowych.

6. Pytania kontrolne

1. Drgania harmoniczne. Składanie drgań harmonicznych.

2. Krzywe Lissajous.

3. Fale mechaniczne i elektromagnetyczne.

4. Równanie fali harmonicznej i natężenie fali.

5. Zjawiska falowe.

137

---