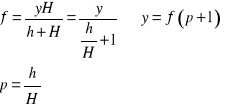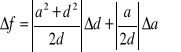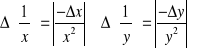Ćwiczenie nr 30

Wyznaczanie ogniskowej skupiającej soczewki cienkiej

1. Cel ćwiczenia

Wyznaczanie ogniskowej skupiającej soczewki cienkiej

2. Wprowadzenie

Soczewką nazywamy przezroczyste ciało ograniczone dwiema powierzchniami kulistymi (sferami) lub jedną powierzchnią kulistą a jedną płaską Promienie kul, które są częściami powierzchni ograniczających soczewkę nazywamy promieniami krzywizn soczewek, a środki tych kul nazywamy środkami krzywizn soczewki. Opisując soczewkę przyjmujemy, że dla soczewki wypukłej promień krzywizny jest dodatni, zaś dla soczewek wklęsłych promień krzywizny przyjmujemy ze znakiem ujemnym. Powierzchnia płaska posiada nieskończony promień krzywizny. Główną osią optyczną soczewki nazywamy prostą przechodzącą przez środki krzywizny obydwu powierzchni. Modelową soczewkę o grubości znacznie mniejszej od promieni krzywizn powierzchni ograniczających soczewkę nazywamy soczewką cienką . W soczewce cienkiej grubość soczewki jest znacznie mniejsza od jej ogniskowej i punkty przecięcia głównej osi optycznej z obu powierzchniami soczewki przypadają praktycznie w tym samym punkcie zwanym środkiem soczewki.

Konstrukcja obrazów w soczewkach

W ośrodkach jednorodnych światło rozchodzi się po liniach prostych. W optyce geometrycznej strumień światła, pochodzący od źródła punktowego, przedstawiamy umownie w postaci promienia świetlnego, którego bieg jest odwracalny. Podstawowymi prawami optyki geometrycznej są prawa odbicia i załamania światła zachodzące na granicy dwóch ośrodków. Prawa te stosujemy przy konstrukcji obrazu w soczewce cienkiej. Soczewkę nazywamy skupiającą , jeżeli promienie równoległe do głównej osi optycznej po przejściu przez soczewkę odchylają się ku osi (rys. 30.1.) , rozpraszającą - jeżeli promienie równoległe do głównej osi optycznej po przejściu przez soczewkę odchylają się od osi (rys 30.2). Promienie przyosiowe (padające pod niewielkim kątem na powierzchnię soczewki w pobliżu jej środka ) biegnące równolegle do głównej osi optycznej , po przejściu przez soczewkę zbierającą skupiają się w jednym punkcie ( F ) zwanym ogniskiem soczewki. Pozorne ognisko soczewki rozpraszającej wyznaczają wsteczne przedłużenia promieni rozproszonych przez soczewkę

Rys 30.1 Soczewka skupiająca

Rys 30.2 Soczewka rozpraszająca

Każda soczewka ma dwa ogniska położone w równych odległościach po obu stronach soczewki. Odległość ogniska od środka soczewki nazywamy ogniskową soczewki i oznaczamy litera f. Punkt wyznaczający ognisko oznaczamy litera F ( od angielskiego Focus) Wartość ogniskowej soczewki określona jest wzorem:

(30.1)

gdzie:

f - ogniskowa soczewki,

n_s - współczynnik załamania materiału z którego zrobiona jest soczewka,

n_o - współczynnik załamania ośrodka otaczającego,

r₁,r₂ -promienie krzywizn soczewek.

Dla soczewek skupiających f > 0, dla rozpraszających f < 0. O tym, czy soczewka jest skupiająca czy rozpraszająca decydują geometria soczewki, materiał, z którego wykonano soczewkę i ośrodek (n_o), w którym soczewka jest umieszczona. Za pomocą soczewek skupiających otrzymujemy obrazy rzeczywiste - powstające w wyniku przecięcia promieni, lub urojone (pozorne) - powstające w wyniku przecięcia przedłużeń promieni. Soczewki rozpraszające pozwalają otrzymać tylko obraz pozorny przedmiotu.

Poniżej na rys.30.3 przedstawiono przykładowy bieg promieni dla soczewki wypukłej. Przedmiot znajduje się pomiędzy ogniskiem a środkiem krzywizny (podwójnym ogniskiem) czyli f < x < 2f .Otrzymano obraz: rzeczywisty, utworzony przez przecięcie promieni świetlnych, odwrócony, powiększony.

Rys 30.3 Przykładowy bieg promieni dla soczewki wypukłej.

Pomiędzy wartościami x, y i f występuje związek, zwany równaniem soczewki:

(30.2)

gdzie:

x - odległość przedmiotu od soczewki

y - odległość obrazu od soczewki

f - ogniskowa soczewki

Powiększenie p definiujemy jako:

(30.3)

gdzie:

H - wysokość przedmiotu

h - wysokość obrazu

Ogniskową soczewki można wyznaczyć kilkoma metodami .

a) Wyznaczanie ogniskowej soczewek metodą graficzną

Metoda polega na pomiarze odległości przedmiotu od soczewki x i odległości obrazu od soczewki y. Dokonujemy pomiarów par punktów (x,y) po uzyskaniu ostrych obrazów przedmiotu. Następnie w prostokątnym układzie współrzędnych odkładamy na osiach odpowiednie wartości x i y i łączymy je odcinkami. Odcinki te przecinają się w jednym punkcie, którego współrzędne (f, f) wyznaczają wartość ogniskowej f. Można również wykonać wykres zależności 1/y = f(1/x). Otrzymany wówczas wykres powinien być malejącą funkcją liniową Y=AX-B, gdzie Y=1/y,X=1/x, zaś wyraz wolny B=1/f. Stąd wartość ogniskowej soczewki skupiającej wynosi 1/B.

b) Wyznaczanie ogniskowej soczewek metodą graficzną wyznaczając powiększenie obrazu

Metoda polega na pomiarze odległości przedmiotu od soczewki x i odległość obrazu od soczewki y wielkości przedmiotu H i wielkości obrazu h. Przesuwając soczewkę wzdłuż ławy optycznej otrzymujemy skupiony , powiększony obraz przedmiotu na ekranie. Po prostych przekształceniach równań 1) i 2) otrzymujmy związek:

	(30.4)
		(30.5)

Zależność y od p+1 jest funkcją liniową Z wykresu zależności y od p+1 wyznaczamy współczynnik kierunkowy prostej, który co do wartości jest równy ogniskowej soczewki f.

c) wyznaczanie ogniskowej soczewek metodą Bessela

Przy stałej odległości przedmiotu od ekranu istnieją dwa położenia soczewki, przy których powstanie ostry obraz przedmiotu. W położeniu pierwszym obraz jest powiększony, a w drugim pomniejszony.

Rys. 30.4 Przykładowy bieg promieni świetlnych przy pomiarze
ogniskowej soczewki metodą Bessela

Dwa położenia soczewki, przy stałej odległości przedmiotu od ekranu, przy których powstanie ostry obraz przedmiotu .

Z oznaczeń na rysunku 30.4 wynikają zależności:

x + y =d	(30.6)
y - x = a	(30.7)

Z układu równań 30.6 i 30.7 otrzymujemy

x = (d-a)/2	(30.8)
y = (d+a)2	(30.9)

Podstawiając otrzymane wartości do wzoru 30.2 otrzymamy zależność między

f i a

f = (d^2-a^2)4d

(30.10)

lub, w innej postaci:

4f = d - (a^2/d)

(30.11)

Metodę Bessela stosować można tylko w przypadku, gdy d > 4f

3. Opis stanowiska laboratoryjnego

Na osi ławy optycznej umieszczone są następujące elementy:

1. źródło światła

2. przedmiot np. w postaci wyciętej w blaszce strzałki

3. soczewka skupiająca

4. ekran

Na ławie optycznej naniesiony jest przymiar liniowy z dokładnością do1 mm

4. Program ćwiczenia

Przy wyznaczaniu ogniskowej soczewki metodą a) i b) dokonujemy pomiaru odległości przedmiotu od soczewki x i odległość obrazu od soczewki y lub wielkości przedmiotu H i wielkości obrazu h. W obu przypadkach wyznaczamy odpowiadające sobie pary punktów (x,y) lub (H,h) i odpowiednio przekształcamy wzór soczewkowy (wzór 30.2.)

a. Wyznaczanie ogniskowej soczewek metodą graficzną

Kolejność czynności:

1. Ustawić źródło światła, przedmiot, soczewkę i ekran na osi ławy optycznej.

2. Przed rozpoczęciem szczegółowych pomiarów oszacować wartość ogniskowej soczewki skupiającej rzucając na nią światło z odległego źródła światła.

3. Ekran ustawiamy w maksymalnej odległości d od przedmiotu.

4. Przesuwając soczewkę wzdłuż ławy optycznej uzyskać ostry obraz przedmiotu. Zanotować wartości x i y i ich niepewności pomiarowe Δx, Δy.

5. Zmniejszyć odległość d o około 5 cm. Powtórzyć pomiary z punktu 4.

6. Powtórzyć czynności z punktów 4. i 5. przynajmniej dla 10 różnych odległości d. Wyniki zanotować w tabeli 30.1.

Tabela 30.1.

Δx = Δy =

1p.	d=x+y[cm]	x[cm]	y[cm]

b) Wyznaczanie ogniskowej soczewek metodą graficzną wyznaczając powiększenie obrazu p

Kolejność czynności:

1. Ustawić źródło światła, przedmiot, soczewkę i ekran na osi ławy optycznej.

2. Przed rozpoczęciem szczegółowych pomiarów oszacować wartość ogniskowej soczewki skupiającej rzucając na nią światło z odległego źródła światła.

3. Ekran ustawiamy w maksymalnej odległości d od przedmiotu.

4. Przesuwając soczewkę wzdłuż ławy optycznej uzyskać ostry obraz przedmiotu. Zanotować wartości x, y, H ,h i ich niepewności pomiarowe Δx, Δy ,ΔH, Δh.

5. Zmniejszyć odległość d o około 5 cm. Powtórzyć pomiary z punktu 4.

6. Powtórzyć czynności z punktów 4. i 5. przynajmniej dla 10 różnych odległości d.

7. Wyniki zanotować w tabeli 30.2.

Tabela 30. 2.

Δx = Δy = ΔH= Δh=

1p.	x[cm]	y[cm]	H[cm]	h[cm]

c) wyznaczanie ogniskowej soczewek metodą Bessela

Kolejność czynności:

1. Ustawić źródło światła, przedmiot, soczewkę i ekran na osi ławy optycznej.

2. Przed rozpoczęciem szczegółowych pomiarów oszacować wartość ogniskowej soczewki skupiającej rzucając na nią światło z odległego źródła światła.

3. Ustawić na ławie optycznej przedmiot i ekran w stałej odległości d

( d >4f)

4. Ustawić położenie soczewki wzdłuż ławy optycznej tak, aby uzyskać ostry obraz powiększony. W tabeli zanotować odległość przedmiotu od soczewki x₁ i odległość soczewki od ekranu y₁.

5. Ustawić położenie soczewki wzdłuż ławy optycznej tak, aby uzyskać ostry obraz pomniejszony. W tabeli zanotować odległość przedmiotu od soczewki x₂ i odległość soczewki od ekranu y₂.

6. Punkty 3- 5 powtórzyć dla innych odległości d przedmiotu od ekranu.

Wyniki zanotować w tabeli 30.3.

Tabela 30.3.

Δd = Δx₁ = Δy₁ = Δx₂ = Δy₂ =

1p.	d[cm]	x1[cm]	y1[cm]	x2[cm]	y2[cm]	a1= y1-x1[cm]	a2= y2-x2 [cm]

5. Sprawozdanie

1. W zależności od metody wykowania ćwiczenia określić maksymalne niepewności systematyczne pomiarów.

2. W metodzie Bessela wyznaczyć wartość ogniskowej ze wzoru (30.10) i maksymalną niepewność systematyczną Δf obliczoną metodą różniczki zupełnej ze wzoru:

(30.12)

3. Sporządzając wykres zależności 1/y=f(1/x) nanieść na wykres niepewności Δ(1/y) i Δ(1/x) obliczone ze wzorów:

(30.13)

Z wykresu wyznaczyć wartość f.

Niepewność pomiarową f wyznaczyć ze wzoru

(30.14)

:

4. Jeżeli sporządzono wykres odcinków par punktów (x,y) zaznaczyć na wykresie prostokąt wokół „rozmytego” punktu przecięcia.

5. Dyskusja wyników i niepewności pomiarowych.

6. Pytania kontrolne

1. Światło i jego właściwości

2. Widmo fal elektromagnetycznych

3. Zjawiska falowe

4. Optyka geometryczna i granice jej zastosowania

183

---