ĆWICZENIA 2 - Finanse przedsiębiorstwa
WARTOŚĆ PIENIĄDZA W CZASIE
Wartość pieniądza w czasie mówi, że posiadana kwota pieniężna ma w dniu dzisiejszym większą wartość niż ta sama kwota w przyszłości (np.: posiadane w dniu dzisiejszym 100 PLN jest warte więcej niż te same 100 PLN otrzymane w przyszłości). Jest to spowodowane tym że:
- pieniądze posiadane dziś mogą zostać zainwestowane i być źródłem zysków
- pożyczając dziś od kogoś pieniądze, będziemy musieli przy ich zwrocie (w przyszłości) zapłacić dodatkowo odsetki
1.1 WARTOŚĆ PRZYSZŁA PIENIĄDZA
Wartość przyszła oznacza kwotę jaką będziemy dysponowali w przyszłości z dziś zainwestowanych środków pieniężnych.
a) Wartość przyszłą płatności jednorazowej przy oprocentowaniu prostym określa następujący wzór:
FV = PV * (1 + n * r)
gdzie:
FV- wartość przyszła pieniądza
PV - aktualna wartość pieniądza (wartość początkowa)
n - liczba okresów naliczania odsetek
r - okresowa stopa procentowa
Zadanie 1
Pan Kowalski ulokował 3 000 PLN swoich oszczędności na lokacie. Oblicz ile pieniędzy będzie miał Kowalski za 3 lata jeżeli roczna stopa oprocentowania tej lokaty wynosi 5%.
b) Wartość przyszłą płatności jednorazowej przy oprocentowaniu złożonym (tj. kapitalizacji) określa następująca formuła:
FV = PV * (1 + r)n
Zadanie 2
Kwotę 5 000 PLN ulokowałeś w banku na rachunku kapitalizowanym raz na kwartał. Ile będziesz miał pieniędzy za 5 lat jeżeli roczna stopa procentowa wynosi 10%?
Zadanie 3
Firma ALEX ulokowała 2 000 PLN w lokacie 5 letniej która jest kapitalizowana półrocznie. W ciągu pierwszych dwóch lat stopa oprocentowania lokaty wynosiła 10% rocznie, w ciągu następnych trzech półroczy 12% rocznie oraz przez pozostały okres 4% kwartalnie. Jaka będzie wartość lokaty po upływie 5 lat?
c) Wartość przyszła stałych okresowych płatności realizowanych z dołu (na koniec każdego okresu) jest wyrażona następującym wzorem:
![]()
gdzie:
FVA - wartość przyszła stałych okresowych płatności
A - wartość jednej okresowej płatności
n - liczba okresów (płatności)
r - okresowa stopa procentowa
Płatności okresowe są strumieniem stałych płatności, występującymi cyklicznie, w jednakowych odstępach czasu a ich wartość jest taka sama
Przykład obliczania przyszłej wartości płatności okresowych realizowanych z dołu
Zadanie 4
Na koniec każdego kwartału wpłacasz do banku po 500 PLN. Roczna stopa procentowa wynosi 12%, a odsetki kapitalizowane są kwartalnie. Ile zgromadzisz pieniędzy po trzech latach inwestowania?
d) Wartość przyszła stałych okresowych płatności realizowanych z góry (na początek każdego okresu) jest wyrażona następującym wzorem:
![]()
Zadanie 5
Na początku każdego miesiąca wpłacasz 100 PLN na rzecz funduszu inwestycyjnego. Odsetki zgromadzone na koncie funduszu są kapitalizowane każdego miesiąca a roczna ich stopa oprocentowania wynosi 24%. Ile pieniędzy zgromadzisz po 2 latach oszczędzania?
1.2. WARTOŚĆ OBECNA PIENIĄDZA
a) Wartość obecna oznacza ile obecnie jest warta kwota pieniężna, którą otrzymamy w przyszłości. Wartość obecna płatności jednorazowej przy założeniu stałej oczekiwanej stopy zwrotu jest wyrażone następującym wzorem:
![]()
gdzie:
PV - obecna wartość pieniądza
FV - oczekiwana wartość przyszła pieniądza
n- liczba okresów
r - oczekiwana okresowa stopa zwrotu
Zadanie 6
Za trzy lata otrzymasz kwotę 10 000 PLN. Oblicz obecną wartość tej kwoty jeżeli wiadomo, że okresowa stopa zwrotu wynosi 10%.
Zadanie 7
Pan Nowak kupiła samochód na raty. W momencie zakupu wpłacił sprzedawcy 20 000 PLN, następnie co pół roku będzie wpłacał następujące kwoty:
- 15 000 PLN,
- 10 000 PLN,
- 5 000 PLN.
Jaka jest obecna wartość transakcji, jeżeli oczekiwana roczna stopa zwrotu wynosi 12% rocznie.
b) Wartość obecna stałych okresowych płatności realizowanych z dołu (na koniec każdego okresu) jest wyrażona następującym wzorem:
![]()
gdzie:
PVA - wartość obecna stałych okresowych płatności
A- wartość jednej okresowej płatności
n - liczba okresów (płatności)
r- okresowa stopa procentowa
Przykład obliczania obecnej wartości płatności okresowych realizowanych z dołu
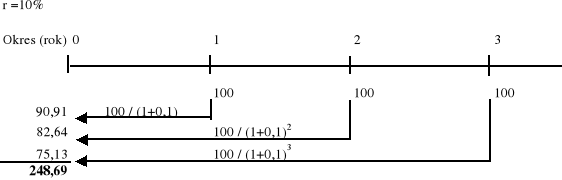
Zadanie 8
Nabywca rozważa zakup pewnego dobra w pięciu rocznych płatnościach po 500 PLN, ponoszonych na koniec każdego roku. Stopa dyskontowa wynosi 10%. Oblicz wartość bieżącą tych pięciu płatności.
c) Wartość obecna stałych okresowych płatności realizowanych z góry (na początek każdego okresu) jest wyrażona następującym wzorem:
![]()
Zadanie 9
Musisz spłacić zaciągnięty w banku kredyt. Bank proponuje Ci dwa warianty spłaty kredytu:
spłatę stałymi płatnościami każda o wartości 1 000 PLN, płatnymi na początek każdego miesiąca przez okres dwóch lat, przy rocznej stopie dyskontowej w wysokości 12%
spłata za rok 10 000 PLN, przy rocznej stopie dyskontowej w wysokości 12%
Wybierz wariant korzystniejszy.
STOPA ZWROTU Z ZAANGAŻOWANYCH KAPITAŁÓW
Stopa zwrotu jest relacją wartości zysku osiągniętego z inwestycji oraz wartości zaangażowanego w nią kapitału. Zysk z inwestycji powstaje z dwóch źródeł:
- zmiany wartości aktywa w które zaangażowano kapitał
- bieżących wpływów osiągniętych z tego aktywa (odsetki, dywidendy)
Stopę zwrotu z kapitałów zaangażowanych w dowolne aktywo można ustalić wykorzystując poniższy wzór:
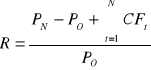
gdzie:
PN - wartość aktywa na koniec okresu inwestycji,
PO - początkowa wartość aktywa
![]()
- suma wpływów z inwestycji w okresie jej wykonania
Zadanie 10
Trzy lata temu kupiłeś akcje pewnej spółki za kwotę 5 000 PLN. W kolejnych latach otrzymywałeś dywidendy w kwocie 100 PLN w pierwszym roku, 200 PLN w drugim roku oraz 500 PLN w trzecim roku. Obecnie wartość nabytych trzy lat temu akcji wynosi 6 500 PLN. Oblicz stopę zwrotu z okresu trwania inwestycji.
METODY WYCENY AKTUALNEJ WARTOŚCI AKTYWÓW FINANSOWYCH
WARTOŚĆ BIEŻĄCA OBLIGACJI
Obligacja jest dłużnym papierem wartościowym. Poprzez ten instrument finansowy emitent (wystawca) obligacji zaciąga pożyczkę u właściciela obligacji. Emitent zobowiązuje się do zwrotu zaciągniętej w ten sposób pożyczki oraz do zapłaty odsetek z tytułu powstałego zobowiązania. Wartość obecną obligacji ustala się na podstawie dyskontowania oczekiwanych w przyszłych okresach, odsetek płatnych właścicielowi obligacji oraz dyskontowania wartości obligacji płatnej przez emitenta przy jej wykupie. Wzór na ustalenie wartości bieżącej obligacji wygląda następująco:
![]()
gdzie:
VB - wartość bieżąca obligacji kuponowej
I t - wartość odsetek z obligacji płatnych w okresie t
NVB - wartość nominalna obligacji
r - okresowa oczekiwana stopa zwrotu z inwestycji
Zadanie 11
Inwestujesz w trzyletnią obligację o wartości nominalnej 1 000 PLN. Oprocentowanie tej obligacji wyniesie w pierwszym roku 8%, w roku drugim 7% oraz w trzecim roku 6%. Twoja oczekiwana stopa zwrotu wynosi 10% rocznie. Oblicz wartość bieżącą tej obligacji.
WARTOŚĆ BIEŻĄCA AKCJI
Wartość akcji jest określona jako wartość obecna przyszłych wpływów, możliwych do osiągnięcia z jednej akcji. Wpływami z akcji są dywidendy oraz wartość akcji, jaką można otrzymać przy jej sprzedaży. W związku z tym, że zarówno przyszłe dywidendy oraz przyszła wartość akcji są w dniu wyceny nieznane i niepewne, do ustalania wartości bieżącej akcji stosuje się najczęściej model Gordona - stałego wzrostu dywidendy, który opisujemy następującym wzorem:
![]()
gdzie:
DPS1 - oczekiwana wartość dywidendy na jedną akcję zwykłą w roku następnym
DPS0 - ostatnio wypłacona dywidenda na jedną akcję zwykłą
re - okresowa oczekiwana stopa zwrotu z inwestycji o tym samym ryzyku
g - prognozowana stała stopa wzrostu zysków i dywidend spółki
Zadanie 12
Oblicz wartość bieżącą akcji zwykłej firmy LUX, która w ostatnim roku wypłaciła dywidendę na jedną akcję w wysokości 5 PLN. Stopa zwrotu z alternatywnych inwestycji o tym samym ryzyku wynosi 10% rocznie, a prognozowana stopa wzrostu dywidend spółki kształtuje na poziomie 8%.
Oprocentowanie proste występuje wtedy, gdy odsetki obliczane są od kwoty pierwotnie zainwestowanej
Oprocentowanie złożone występuje wtedy, gdy odsetki obliczane są od kwoty pierwotnie zainwestowanej oraz od wszystkich wcześniej naliczonych odsetek.
Piotr J. Szczepankowski, Zarządzanie finansami przedsiębiorstwa. Podstawy teoretyczne, przykłady i zadania, Warszawa, WSPiZ 2004, s. 67
2
Wyszukiwarka