XIV. Hydroliza soli. Sole trudno rozpuszczalne

XIV.1. Hydroliza soli pochodzących od słabych
elektrolitów

Roztwory soli mocnych kwasów i mocnych zasad mają zawsze odczyn obojętny i pH = 7, ponieważ sole te nie ulegają hydrolizie. Hydroliza jest wtórnym procesem decydującym o tym, że roztwory soli słabych zasad i mocnych kwasów mają odczyn kwaśny i pH < 7, natomiast roztwory słabych kwasów i mocnych zasad mają odczyn zasadowy
i pH > 7.

Hydroliza jest reakcją kationów soli słabej zasady lub anionów soli słabego kwasu z wodą.

Proces hydrolizy soli w roztworach wodnych ma charakter odwracalny i podlega prawu działania mas. Stany równowag w roztworach soli charakteryzują stałe hydrolizy, Kh. Stałych hydrolizy nie podaje się w tablicach!

XIV.1.1. Hydroliza soli słabej zasady (BOH) i mocnego
kwasu (HX)

Typowymi przykładami są sole amonowe: NH4Cl, NH4ClO4, NH4NO3, (NH4)2SO4. Ogólnie sole typu BX.

BX → B+ + X- (dysocjacja)

B+ + H2O ↔ BOH + H+ (hydroliza)

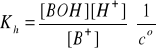
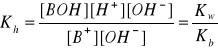
pKh = pKw - pKb

Stopień hydrolizy (β) soli zależy od jej stężenia (cs) w roztworze i wzrasta wraz jego rozcieńczeniem. Świadczy to, że hydroliza soli podlega prawu rozcieńczeń Ostwalda:

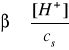
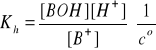
Bilans stężeń w stanie równowagi:

[H+] = [BOH] = β·cs

[B+] = cs - [H+] = cs - β·cs = cs(1- β)

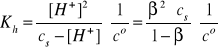
Gdy cs >> [H+], to β << 1, a w konsekwencji mamy:

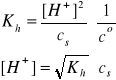
i/lub

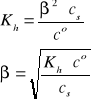
Uwaga: W przypadku (NH4)2SO4, analityczne stężenie kationów NH4+ jest dwukrotnie większe od stężenia tej soli. W roztworze dwóch soli amonowych, np. NH4Cl (cs1) i NH4NO3 (cs2), analityczne stężenie kationów NH4+ jest równe sumie stężeń (cs1 + cs2) obydwu soli.

XIV.1.2. Hydroliza soli słabego kwasu (HA) i mocnej
zasady (MOH)

Typowe przykłady to NaHCOO - mrówczan sodu,

NaCH3COO - octan sodu, KNO2 - azotan(III) potasu,

NaClO - chloran(I) sodu, NaCN - cyjanek sodu. Ogólnie sole typu MA.

MA → M+ + A- (dysocjacja)

A- + H2O ↔ HA + OH- (hydroliza)

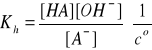
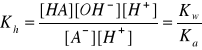
pKh = pKw - pKa

Tak, jak w poprzednim przypadku, hydroliza podlega prawu rozcieńczeń Ostwalda, ponieważ stopień hydrolizy (β) soli zależy od jej stężenia (cs)
w roztworze i wzrasta wraz jego rozcieńczeniem.

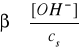
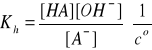
Bilans stężeń w stanie równowagi:

[OH-] = [HA] = β·cs

[A-] = cs - [OH-] = cs - β·cs = cs(1- β)

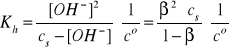
Gdy cs >> [OH-], to β << 1, a w konsekwencji mamy:

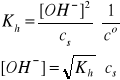
i/lub

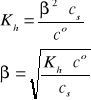
Uwaga: W przypadku soli CaA2, np. octanu wapnia, analityczne stężenie anionów octanowych jest dwukrotnie większe od stężenia tej soli. W roztworze dwóch soli, np. NaNO2 (cs1) i KNO2 (cs2), analityczne stężenie anionów NO2- jest równe sumie stężeń (cs1 + cs2) obydwu soli.

XIV.1.3. Hydroliza soli słabych kwasów i słabych zasad

Typowe przykłady to NH4NO2, NH4CH3COO, NH4CN. Ogólnie sole typu BA. W roztworach tych soli hydrolizuje zarówno kation B+, jak i anion A-.

B+ + H2O ↔ BOH + H+

A- + H2O ↔ HA + OH-

Stopień hydrolizy soli AB nie zależy od jej stężenia
w roztworze:

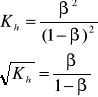
Natomiast odczyn roztworów soli AB zależy od stosunku stałych dysocjacji słabego kwasu HA
i słabej zasady BOH.

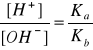
pH - pOH = pKa - pKb,

pH + pOH = pKw,

stąd

pH = (pKw + pKa - pKb)/2.

Przykłady:

1. Obliczyć stopień hydrolizy i pH 0,010 M octanu sodu.

cs = 0,010 mol/dm3, pKa = 4,79, pKw = 14,00

NaCH3COO → Na+ + CH3COO-

CH3COO- + H2O ↔ CH3COOH + OH-

pKh = pKw - pKa = 9,21, Kh = 10-9,21 = 6,17·10-10

Założenie: β << 1

Wynik jest poprawny, ponieważ założenie jest spełnione.

[OH-] = β·cs = 2,5·10-6 mol/dm3

pOH = 5,60

pH = 14,00 - 5,60 = 8,40

2. Obliczyć stopień hydrolizy i pH 0,010 M chlorku amonu.

cs = 0,010 mol/dm3, pKb = 4,75, pKw = 14,00

pKh = pKb - pKa = 9,25, Kh = 10-9,25 = 5,62·10-10

NH4Cl → NH4+ + Cl-

NH4+ + H2O ↔ NH4OH + H+

Założenie: β << 1

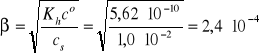
Wynik jest poprawny, ponieważ założenie jest spełnione.

[H+] = β·cs = 2,4·10-6 mol/dm3

pH = 5,62

3. Obliczyć pH roztworu octanu amonu NH4CH3COO.

pKw = 14,00, pKa = 4,79, pKb = 4,75

pH = (pKw + pKa - pKb)/2

pH = (14,00 + 4,79 - 4,75)/2 = 7,02

XIV.2. Sole trudno rozpuszczalne

Oprócz elektrolitów dobrze rozpuszczających się
w wodzie, znamy liczną grupę soli i wodorotlenków metali, których rozpuszczalność w wodzie jest mała lub znikoma. Rozpuszczalność danego związku, rozumiana jako stężenie w roztworze nasyconym, zależy od temperatury.

W porównaniu ze związkami dobrze rozpuszczalnymi, rozpuszczalność (R) - czyli stężenie trudno rozpuszczalnego związku w jego roztworze nasyconym jest znikoma. W każdym przypadku
stały, trudno rozpuszczalny elektrolit, AmBn, nie rozpuszcza się już w jego roztworze nasyconym
w danej temperaturze. Oznacza to, że między tym elektrolitem w fazie stałej i jego roztworem nasyconym ustala się stan równowagi:

AmBn ↔ mAn+ + nBm-

faza stała roztwór nasycony

Stan równowagi w tym układzie determinuje rozpuszczalność R, czyli stężenie związku
w roztworze nasyconym, co wyrażamy za pomocą stałej równowagi zwanej iloczynem rozpuszczalności Ir tego związku. Iloczyn rozpuszczalności związku AmBn jest iloczynem stężeń jonów An+ i Bm- w roztworze nasyconym:

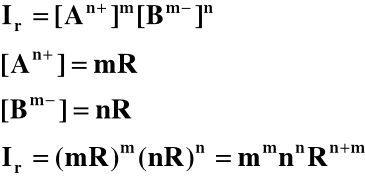
-log Ir = pIr

Jako przykład rozpatrzymy trudno rozpuszczalny
w wodzie fosforan(V) wapnia, Ca3(PO4)2, dla którego mamy:

Ir = (3R)3(2R)2 = 108R5 = 1,0∙10-26

Na tej podstawie możemy obliczyć rozpuszczalność tego związku w wodzie:

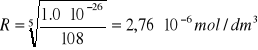
Rozpuszczalność związków trudno rozpuszczalnych, soli lub wodorotlenków, w roztworach elektrolitów różni się od rozpuszczalności tych związków
w czystej wodzie. Przyczyną tego zjawiska są dwa efekty, mianowicie efekt solny i efekt wspólnego jonu.

Efekt solny

Rozpuszczalność trudno rozpuszczalnego związku w roztworach soli nie mającej z nim wspólnego jonu jest zawsze większa od jego rozpuszczalności w czystej wodzie.

Naturę efektu solnego rozpatrzymy na przykładzie chlorku srebra AgCl, którego pIr jest równy 9,75.

AgCl ↔ Ag+ + Cl-

faza stała r-r nasycony

Ir = 10-9,75 = 1,78∙10-10

Gdy chlorek srebra rozpuści się w czystej wodzie, to jego rozpuszczalność jest równa R :

[Ag+] = [Cl-] = R

Ir = [Ag+][Cl-] = R2

R = (Ir)1/2 = 1,33∙10-5 mol/dm3

Natomiast rozpuszczalność R' chlorku srebra
w 0,01 M roztworze KNO3, który nie ma
z chlorkiem srebra wspólnego jonu, jest nieco większa niż w wodzie. Wynika to z faktu, że
w czystej wodzie współczynniki aktywności jonów, yAg+ i yCl-, są równe 1, natomiast w 0,01 M roztworze KNO3 są równe 0,857.

Ir = yAg+·yCl-[Ag+][Cl-] = yAg+·yCl-(R')2

R' = 1,56∙10-5 mol/dm3

Efekt wspólnego jonu

Ponownie rozpatrzymy chlorek srebra. Tym razem postawimy pytanie o jego rozpuszczalność R' w 0,10 M chlorku sodu, NaCl, który z chlorkiem srebra ma wspólny anion. W tym przypadku
w uzyskanym roztworze nasyconym mamy:

[Ag+] = R'

[Cl-] = R' + cNaCl

Ir = R'(R' + cNaCl)

Zakładając, że cNaCl >> R' otrzymujemy

Ir = R' cNaCl

,

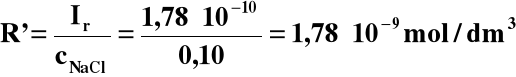
co pozostaje w bardzo dobrej zgodności z przyjętym założeniem, ponieważ rozpuszczalność chlorku srebra zmalała około 7500 razy.

Uzyskany wynik upoważnia do ogólnego wniosku, że elektrolity o wspólnym jonie zmniejszają rozpuszczalność trudno rozpuszczalnego związku nawet o kilka rzędów wielkości względem jego rozpuszczalności w czystej wodzie. Potwierdza to również przedstawiony niżej przykład.

Przykład

Porównać rozpuszczalność wodorotlenku Mn(II)
w czystej wodzie i 0,01 M NaOH. pIr Mn(OH)2 jest równy 12,72.

Mn(OH)2 ↔ Mn2+ + 2OH-

faza stała roztwór nasycony

Ir = 10-12,72 = 1,9∙10-13

Rozpuszczalność w czystej wodzie:

[Mn2+] = R, [OH-] = 2R

Ir = R∙(2R)2 = 4R3

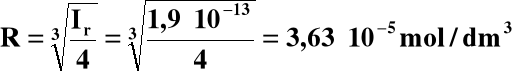
Rozpuszczalność w 0,01 M NaOH:

[Mn2+] = R', [OH-] = 2R' + cNaOH

Ir = R'∙(2R' + cNaOH)

Założenie: cNaOH >> 2R'

Ir = cNaOH∙R'

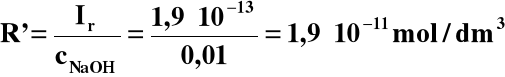
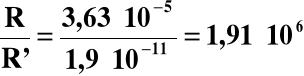
Jak widać, rozpuszczalność Mn(OH)2 w 0,01 M NaOH jest około dwa miliony razy mniejsza od rozpuszczalności w czystej wodzie.

Omawiane na dzisiejszym wykładzie tematy mają ważne znaczenie praktyczne w chemii analitycznej. Hydroliza soli w roztworach wzorcowych, czyli roztworach o ściśle określonym stężeniu jonów danego rodzaju, jest zjawiskiem niepożądanym. Przykładowo, hydroliza roztworów wzorcowych o dokładnie znanym stężeniu kationów Fe3+ prowadzi do wytrącenia się trudno rozpuszczalnego wodorotlenku Fe(OH)3. Z tego powodu roztwory soli Fe(III) zakwasza się kwasem solnym lub siarkowym(VI), co zgodnie z regułą przekory zapobiega reakcji hydrolizy.

Efekt wspólnego jonu na rozpuszczalność związków trudno rozpuszczalnych wykorzystuje się w analizie wagowej (grawimetria) i analizie miareczkowej (precypitometria), ponieważ w obydwu przypadkach pożądana jest jak najmniejsza rozpuszczalność trudno rozpuszczalnego związku, stanowiąca podstawę oznaczeń grawimetrycznych, np. baru jako BaSO4, żelaza jako Fe2O3, lub oznaczeń precypitometrycznych, np. srebra jako AgCl.

---