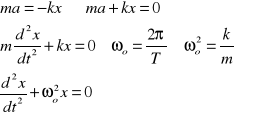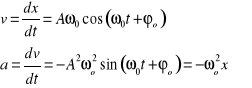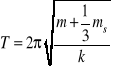Ćwiczenie nr 10

BADANIE ZALEŻNOŚCI WYDŁUŻENIA SPRĘŻYNY OD OBCIĄŻENIA

1. Cel ćwiczenia

Wyznaczenie stałej sprężystości sprężyny metodą statyczną. Sprawdzenie prawa Hooke`a.

2. Wprowadzenie

W ruchu harmonicznym prostym siła działająca na drgające ciało F jest wprost proporcjonalna do wychylenia z położenia równowagi x i zwrócona w stronę położenia równowagi:

(10.1)

gdzie k oznacza stałą proporcjonalności, masę ciała.

Warunek ten spełnia sprężyna obciążoną masą m i dodatkowo wychylona od położenia równowagi. Korzystając z II zasady dynamiki można powyższe równanie przekształcić następująco:

	(10.2)
		(10.3)
		(10.4)

Rozwiązaniem równania różniczkowego:

(10.5)

jest funkcja periodyczna typu sinus lub cosinus:

(10.6)

gdzie:

x(t) - wychylenie z położenia równowagi po czasie t,

A - amplituda czyli maksymalne wychylenie,

ω_o - częstość kątowa drgań,

T - okres drgań,

φ_o - faza początkowa drgań.

Prędkość v i przyśpieszenie a w tym ruchu zmienia się również w sposób periodyczny:

	(10.7)
		(10.8)

gdzie:

k - w przypadku sprężyny k oznacza stałą sprężystości,

x - wychylenie od położenia równowagi (statyczne).

Okres takich drgań wyrażamy wzorem:

(10.9)

W dokładniejszych obliczeniach, zwłaszcza gdy masa sprężyny m_s jest porównywalna z masą obciążnika, uwzględniamy tak zwaną efektywną masę sprężyny
m_ef = 1/3m_s ,która również uczestniczy w drganiach harmonicznych. Wówczas okres takich drgań wyrażamy wzorem:

(10.10)

Ciała wykonujące drgania harmoniczne nazywamy oscylatorem harmonicznym.

3. Opis stanowiska laboratoryjnego

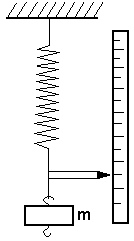
Wahadło matematyczne, statyw do zawieszania wahadła, przymiar liniowy, stoper.

Rys. 10.1 Układ pomiarowy

4. Program ćwiczenia:

1. Zawiesić sprężynę na stojaku i na miarce odczytać położenie zerowe końca sprężyny nieobciążonej x_o.

2. Obciążyć sprężynę odważnikiem o masie m₁ i zanotować w tabeli położenie końca sprężyny x₁.

3. Powyższą czynność powtórzyć dla przynajmniej 6-u mas dodając do masy m₁ koleje obciążniki ( zakres mas skonsultować z prowadzącym zajęcia). Wyniki zapisać w tabeli 10.1.

4. Wyliczyć dla każdego pomiaru Δx_i = xi - x_o i siłę F_i = m_ig [N]

5. Wyznaczyć niepewności pomiarowe Δx_i ,Δm_i , ΔF_i .

Uwaga: Czy niepewność pomiarowa Δm_i, ΔF_i zależy od sposobu pomiaru mas. (masa bieżąca podawana jako suma mas pojedynczych obciążników czy masa zważonych razem obciążników)

Tabela 10.1

Δx_i = Δm_i = ΔF= _i

l.p.	mi [kg]	Σ mi [kg]	Σ mi [kg]	xo [m]	xi [m]	Δxi [m]	Δxi [m]	Fi = mig [N]

5. Sprawozdanie

1. Korzystając z programu regresja liniowa lub korzystając z arkusza kalkulacyjnego Excel sprawdzić liniowość wykresu F = f(Δx_i) oraz zapisać wyliczone przez program współczynniki regresji a, b, Sa, Sb, r.

2. Na papierze milimetrowym wykonać wykres F= f(Δx_i), zaznaczyć na wykresie prostokąty niepewności pomiarowych i poprzez maksymalna ilość prostokątów poprowadzić prostą. Z wykresu wyznaczyć współczynnik kierunkowy prostej. Podać sens fizyczny otrzymanego współczynnika.

3. Powyższe czynności powtórzyć dla kolejnych sprężyn o innych właściwościach.

Przeprowadzić dyskusję otrzymanych wyników.

6. Pytania kontrolne

1. Drgania harmoniczne proste i tłumione.

2. Wykresy wychylenia, prędkości i przyspieszenia w ruchu harmonicznym.

3. Ciężar i masa.

4. Energia w ruchu harmonicznym.

5. Podaj przykłady układów spełniających warunek ruchu harmonicznego.

69

---