Wyznaczanie ΔG, ΔH oraz ΔS reakcji chemicznej

Pomiar odwracalnej wartości siły elektromotorycznej orz znajomość reakcji sumarycznej umożliwiają bezpośrednie i dokładne obliczenie potencjału termodynamicznego reakcji. Jeżeli w reakcji bierze udział liczba elektronów n razy większa od liczby Avogadra przepływowi nF kulombów ładunku odpowiada zmiana potencjału termodynamicznego określona wzorem:

∆G = - nFE

Powyższe równanie daje się prosto wyprowadzić rozważając ogniwo chemiczne w którym przebiega reakcja sumaryczna: aA + bB ⇔ cC + dD.

Potencjał termodynamiczny 1 mola substancji A można określić wzorem:

natomiast potencjał termodynamiczny a moli tej substancji wzorem:

Wyprowadzając powyższe równania dla wszystkich reagentów A, B, C i D, można wyznaczyć potencjał termodynamiczny sumarycznej reakcji ogniwa, który wyniesie odpowiednio:

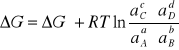
gdzie: ∆G° oznacza różnicę między potencjałami termodynamicznymi produktów i substratów, gdy wszystkie reagenty znajdują się w swoich stanach standardowych.

Zgodnie z równaniem Nernsta siła elektromotoryczna omawianego ogniwa będzie równa:

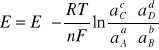
Z porównania obydwu wzorów otrzymujemy prosty wzór na zmianę potencjału termodynamicznego:
i
. Czyli określając zależność SEM od temperatury można wyznaczyć entropię i ciepło reakcji.

Znając termodynamiczną zależność entropii z potencjałem termodynamicznym, czyli:

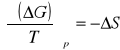
i podstawiając wcześniej wyprowadzone równanie otrzymujemy wzór postaci:

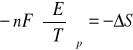
, czyli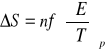

który umożliwia obliczenie entropii reakcji na podstawie współczynnika temperaturowego siły elektromotorycznej ogniwa. Korzystając zaś z kolejnej zależności postaci:
możemy obliczyć entalpię reakcji w danej temperaturze. Zatem pomiar SEM i jej współczynnika temperaturowego umożliwiają określenie ∆G, ∆H i ∆S dla przebiegającej w ogniwie reakcji. Drogą pomiarów SEM uzyskuje się więc wiele informacji termodynamicznych o wodnych roztworach jonowych.

W doświadczeniu jakie będziemy przeprowadzać zmierzymy wartość E w kilku temperaturach w ogniwie Clarka i na podstawie tych danych wyznaczymy G, H i S reakcji, jaka w nim zachodzi.

Pomiary i obliczenia

• W doświadczeniu wykorzystaliśmy ogniwo Clarka o schemacie:

(-) Zn (Hg), ZnSO₄∙7H₂O (roztwór nasycony) | Hg₂SO₄ (s), Hg (+)

którego źródłem siły elektromotorycznej jest reakcja:

Zn + Hg₂SO₄ + 7H₂O = ZnSO₄∙7H₂O + 2Hg

• Pomiaru SEM w ogniwie Clarka dokonaliśmy w zakresie temperatur od 0°C do 40°C (co dziesięć stopni) przy pomocy woltomierza. W każdej temperaturze ogniwo termostatowało się przez około 10-15 minut (wskazania przez woltomierz były stabilne).

• Uzyskaliśmy następujące wyniki, według których sporządzono wykres SEM = f(t)

temperatura [°C]	0	10	20	30	40
SEM [mV]	1395	1378	1362	1351	1340

• Na podstawie powyższych danych program komputerowy dokonał obliczeń G, H i S:

temp. [°C]	G [J/mol]	H [J/mol]	S [J/mol∙K]
0	-2,692∙10^5	-3,414∙10^5	-2,644∙10^2
10	-2,659∙10^5	-3,407∙10^5	-2,644∙10^2
20	-2,628∙10^5	-3,403∙10^5	-2,644∙10^2
30	-2,607∙10^5	-3,408∙10^5	-2,644∙10^2
40	-2,586∙10^5	-3,413∙10^5	-2,644∙10^2

Wnioski:

• Na podstawie wyników pomiarów oraz sporządzonego wykresu wynika, że zmiana SEM ogniwa w badanym zakresie temperatur jest liniowa oraz, że ze wzrostem temperatury siła elektromotoryczna ogniwa maleje. Zależność jest obarczona niewielkim błędem (nie wszystkie punkty leżą dokładnie na wspólnej prostej), który w naszym doświadczeniu wyniósł 0,0023. Informuje on jednak, że doświadczenie zostało wykonane dokładnie.

• Potencjał termodynamiczny jest funkcją, której wartość oblicza się, aby uzyskać informacje o tym, czy dana reakcja może zachodzić w określonych warunkach. Ze znaczą wydajnością mogą zachodzić tylko takie procesy, w których następuje zmniejszenie potencjału termodynamicznego, tzn. takie, w których ΔG<0. W każdej z badanych temperatur zmiana potencjału termodynamicznego dla reakcji biegnącej w ogniwie Clarka jest wartością ujemną. Oznacza to, że powyższa reakcja jest procesem samorzutnym i możliwym do zrealizowania w tych warunkach.

• Zmiana entalpii w badanym zakresie temperatur również ma wartość ujemną ΔH<0 co oznacza, że reakcja jest egzotermiczna, czyli z wydzieleniem ciepła do otoczenia.

• Jak można zauważyć wartość S jest taka sama niezależnie od temperatury. Zmiana entropii układu, w którym zachodzi reakcja chemiczna, nie świadczy jednoznacznie o kierunku przebiegu przemiany samorzutnej. W każdej przemianie obowiązuje warunek wzrostu entropii, ale dotyczy on całkowitej zmiany entropii układu wraz z otoczeniem. Trudno jest zmierzyć jednak entropię otoczenia. Ponieważ jednak wiemy z zasady termodynamiki, że całkowita entropia musi rosnąć, zatem pewne jest, że w trakcie przebiegu reakcji wzrosła entropia otoczenia.

• Czynnik entropowy przybiera wartości mniejsze od zera, ale jest większy od ΔH. Gdyby TΔS był większy od zera, to potencjał termodynamiczny byłby równy bądź większy od zera. W pierwszym przypadku układ znajdowałby się w stanie równowagi, zaś w drugim proces przebiegałby samorzutnie w kierunku przeciwnym.

- 2 -

---