![]()
Wydział EAIiE
|
|
Zespół 3 |
|||
Grupa 2 |
Temat: Interferencja Fal Akustycznych |
Ćwiczenie nr 25 |
|||
Data wykonania
|
Data oddania
|
Zwrot do popr.
|
Data oddania
|
Ocena
|
Podpis
|
Cel ćwiczenia:
Celem ćwiczenia jest wyznaczenie prędkości rozchodzenia się dźwięku w gazach w temperaturze pokojowej metodą interferencji fal akustycznych przy pomocy rury Quinckego.
Wprowadzenie:
Falą nazywamy zaburzenie stanu ośrodka lub pola elektromagnetycznego, rozchodzące się w przestrzeni ze skończoną prędkością i niosące ze sobą energie. Fale umożliwiają przepływ energi na duże odległości. Przepływowi energi nie towarzyszy przy tym przepływ masy. Przykładem fal są światło i dźwięk. Światło jest falą elektromagnetyczną, natomiast dźwięk falą sprężystą.
Fale elektromagnetyczne są zaburzeniami stanu pola elektromagnetycznego, natomiast fale sprężyste są to zaburzenia stanu ośrodków materialnych :
-w gazach - zaburzenia gęstości
-w cieczach - zaburzenia gęstości lub zaburzenia kształtu powierzchni swobodnej
-w ciałach stałych - zaburzenia gęstości lub kształtu
W ciałach stałych mogą się rozchodzić fale poprzeczne i podłużne, w cieczach i gazach tylko podłużne. Za fale dźwiękową uważamy fale o częstotliwości od 20 Hz do 20 kHz, gdyż są one słyszalne przez ludzkie ucho. Są również infra i ultra dźwięk.
W ośrodkach zupełnie jednorodnych fale rozchodzą się prostoliniowo, ze stałą prędkością.
Rozchodzenie się dźwięku opisuje równanie falowe. W przypadku gdy źródłem fali dźwiękowej jest układ wykonujący drgania harmoniczne powstaje fala sinusoidalna. Amplituda takiej fali rozchodzącej się wzdłuż drogi x dana jest wzorem:
![]()
gdzie : ![]()
![]()
Gdy w pewnym punkcie przestrzeni spotykają się dwie lub więcej fal, w wyniku ich sumowania zachodzi zjawisko interferencji. Mając dwie fale, które wyszły z tego samego źródła i do odbiornika docierają dwiema różnymi drogami różnej długości x1 i x2.:
y1=ym1sin(kx1-ϖt)
y2=ym2sin(kx2-ϖt)
ich superpozycja (suma) wynosi:
y=y1+y2
Wyznaczenie długości fali λ ze zjawiska interferencji umożliwia przy znajomości częstotliwości f obliczenie prędkości rozchodzenia się fali ze wzoru:
V=fλ
Prędkość dźwięku w gazach dana jest wzorem :
![]()
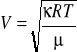
gdzie:
T- temperatura bezwzględna
R- uniwersalna stała gazowa
μ- ciężar cząsteczkowy molekuł gazu
κ- stosunek ciepła właściwego przy stałym ciśnieniu Cp do ciepła właściwego przy stałej objętości Cv.
Pomiar prędkości dźwięku jest standardową metodą wyznaczania wielkości κ.
W ćwiczeniu źródłem jest membrana głośnika, pobudzana do drgań za pomocą generatora częstotliwości akustycznych 20Hz - 20kHz. Częstotliwość tych drgań odczytuje się na skali generatora. Fala dźwiękowa wprowadzona do jednego ze wspólnych końców rur rozdziela się na dwie fale , z których każda biegnie w innej rurze. Fale te spotykają się u wspólnego wylotu rury i tam interferują. Detektorem jest mikrofon węglowy. W słuchawkach słyszymy dźwięk, którego natężenie zależy od różnicy długości rur. Maksymalne wyciszenie dźwięku obserwujemy , gdy różnica długości rur jest nieparzystą wielokrotnością połówki długości fali., czyli odległość kolejnych minimów mierzona jest na skali przyrządu odpowiadającej połowie długości fali.
Częstotliwość |
Położenie |
|
|
|
|
Różnica położeń |
|
|
|
Długość |
Prędkość |
[Hz] |
Kolejnych minimów [mm] |
|
|
|
|
kolejnych minimów [mm] |
|
|
|
fali [m] |
fali [m/s] |
|
a1 |
a2 |
a3 |
a4 |
a5 |
A1 |
A2 |
A3 |
A4 |
|
|
600 |
|
|
|
|
|
|
|
|
|
|
|
700 |
|
|
|
|
|
|
|
|
|
|
|
800 |
|
|
|
|
|
|
|
|
|
|
|
900 |
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
|
|
2000 |
|
|
|
|
|
|
|
|
|
|
|
2100 |
|
|
|
|
|
|
|
|
|
|
|
2200 |
|
|
|
|
|
|
|
|
|
|
|
2300 |
|
|
|
|
|
|
|
|
|
|
|
2400 |
|
|
|
|
|
|
|
|
|
|
|
2500 |
|
|
|
|
|
|
|
|
|
|
|
2600 |
|
|
|
|
|
|
|
|
|
|
|
2700 |
|
|
|
|
|
|
|
|
|
|
|
2800 |
|
|
|
|
|
|
|
|
|
|
|
2900 |
|
|
|
|
|
|
|
|
|
|
|
3000 |
|
|
|
|
|
|
|
|
|
|
|
3100 |
|
|
|
|
|
|
|
|
|
|
|
3200 |
|
|
|
|
|
|
|
|
|
|
|
3300 |
|
|
|
|
|
|
|
|
|
|
|