Błażej Predko

WIP,=>TRiL

Gr.3

Wyznaczanie współczynnika samoindukcji cewki i pojemności kondensatora.

Ćwiczenie 44

Wprowadzenie

Przepływając przez cewkę, zmieniający się w czasie prąd powoduje powstawanie zmiennego strumienia magnetycznego, który w uzwojeniu cewki będzie indukował SEM. Ten szczególny przypadek zjawiska indukcji elektromagnetycznej, kiedy to SEM indukcji powstaje w tej samej cewce, przez którą płynie zmieniający się prąd, nazywa się samoindukcją lub indukcją własną. Łatwo zauważyć, że podobnie jak w przypadku zjawiska indukcji wzajemnej, strumień odpowiedzialny za powstawanie SEM, równy zΦ, będzie proporcjonalny do prądu płynącego przez cewkę: zΦ=Li.

Zatem

Współczynnik proporcjonalności, zwany indukcyjnością własną cewki, zależy od tych samych czynników co indukcyjność wzajemna. Ponieważ już strumień Φ jest poprzez B- proporcjonalny do liczby zwojów, więc z wzoru zΦ=Li wynika, że indukcyjność własna będzie proporcjonalna do kwadratu liczby zwojów. Indukcyjność własną cewki wyraża się w układzie jednostek SI również w henrach 1H=1V*s*A^-1.Zarówno indukcyjność wzajemna M, jak i indukcyjność własna L mogą zależeć od prądu; nie są one wtedy współczynnikami proporcjonalności . Sytuacja taka ma miejsce wtedy, gdy ośrodek otaczający cewki jest nieliniowy, co oznacza, że związek między wektorami B i H jest nieliniowy. Przykładem takich ośrodków są ferromagnetyki, które z racji dużej wartości przenikalności magnetycznej są często używane jako rdzenie cewek. Dla cewek z rdzeniami ferromagnetycznymi można tylko w przybliżeniu obliczać indukcyjności wzajemne i własne.

Kondensator w obwodzie prądu zmiennego.

Jeżeli podłączymy kondensator szeregowo połączony z żarówką do źródła prądu stałego, żarówka rozbłyśnie tylko na moment, bowiem w obwodzie płynie prąd jedynie do momentu naładowania kondensatora. Po naładowaniu okładek prąd nie płynie-w obwodzie prądu stałego kondensator stanowi praktycznie nieskończenie duży opór. Inaczej jest, jeśli jako źródła prądu użyjemy generatora prądu zmiennego. Wraz ze zmianą prądu w obwodzie zmienia się ładunek na okładkach kondensatora. Na danej okładce może on być dodatni albo ujemny, w zależności od kierunku przepływu prądu. Naprzemienne ładowanie i rozładowywanie się kondensatora w obwodzie umożliwia przepływ prądu, którego amplituda jest proporcjonalna do pojemności kondensatora C, gdyż zgodnie z definicją pojemności, C=Q/U , im większa pojemność tym większy ładunek Q może być zgromadzony na okładkach. Opór pojemnościowy R_c jest więc tym mniejszy im większa jest pojemność C. Gdy mamy źródło prądu sinusoidalnie zmiennego, R_c wyraża się wzorem;

Widzimy że opór pojemnościowy jest także odwrotnie proporcjonalny do częstości kołowej zmian prądu. Im większa wartość ω tym mniejszy ładunek zdąży zgromadzić się na kondensatorze podczas jego ładowania i tym mniejsze będzie napięcie przeciwstawiające się przepływowi prądu.

Jeśli w obwodzie prądu zmiennego występuje opór omowy R i kondensator o pojemności C, to całkowity opór, czyli impedancję ωobliczamy ze wzoru:

Wykonanie ćwiczenia

Wyznaczanie oporu omowego cewki.

W tym celu musimy utworzyć obwód, w którym podłączamy amperomierz do źródła prądu stałego kolejno cewkę, zamykamy obwód podłączając woltomierz do cewki. Podłączamy układ do źródła prądu stałego. Odczytujemy trzykrotnie wartości, zwiększając napięcia i obliczamy opór.

Wyznaczanie współczynnika samoindukcji cewki.

Pomiarów dokonujemy w tym samym układzie. Jednak zasilacz i mierniki uniwersalne przełączamy na pomiar prądu zmiennego. Odczytujemy napięcie i natężenie skuteczne dla trzech napięć wyjściowych zasilacza. Obliczamy dla tych pomiarów współczynniki samoindukcji, a ich średnia wartość jest szukaną wartością współczynnika samoindukcji L=0,236H.

Wyznaczanie impedancji i pojemności kondensatora. Układ pomiarowy jest podobny do poprzednich, jednak zamiast cewki do układu podłączamy kondensator. Podobnie dokonujemy pomiarów i wyliczamy impedancję, a następnie pojemność kondensatora C=25,8 [μF].

Obliczenia

Wyznaczanie oporu omowego cewki

.

Nr. Pomiaru i	1	2	3
Napięcie Ui [V]	6,25	12,49	18,53
Natężenie Ii [A]	3,61	7,22	10,72
Opór Ri [Ω]	1,731	1,729	1,728

Wyznaczanie impedancji i współczynnika samoindukcji cewki

Nr. Pomiaru i	1	2	3
Napięcie Ui [V]	6,41	12,67	18,60
Natężenie Ii [A]	2,69	3,79	4,74
Impedancja Zi [Ω]	2,382	3,343	3,924
Współ. Samoind. Li [H]	0,0052	0,00915	0,0112
Wartość średnia współczynnika samoindukcji L [H]			0,00851

Wyznaczanie impedancji i pojemności kondensatora

Nr. Pomiaru i	1	2	3
Napięcie Ui [V]	6,45	12,81	18,80
Natężenie Ii [A]	2,90	6,00	8,90
Impedancja Zi [Ω]	2,224	2,135	2,112
Poj. Konden. Ci [μF]	1430	1490	1500
Wartość średnia pojemności kondensatora C [μF]			1470,(3)

Rachunek błędu

Maksymalny błąd bezwzględny pomiarów R,Z,L i C obliczamy metodą różniczki zupełnej. Częstotliwość kołową ω traktujemy jako wielkość nie obarczoną błędem pomiaru.

1. Opór cewki R_i:

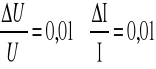
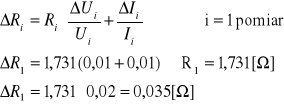
2. Impedancja Z_i:

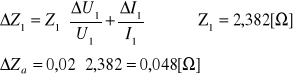
3. Współczynnik samoindukcji L_i:

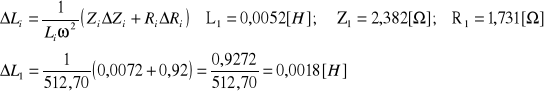
4. Pojemność kondensatora C_i:

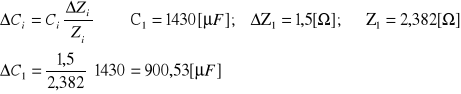
Wnioski

Celem mojego doświadczenia było wyznaczenie współczynnika samoindukcji cewki i pojemności kondensatora. Aby obliczyć te wartości należało wyznaczyć opór omowy, impedencję i współczynnik samoidnukcji cewki oraz impedencję i współczynnik samoindukcji kondensatora.

Moim zdaniem konkretne wnioski nie są tu potrzebne ponieważ moim celem było jedynie sprawdzenie tych wartości.

---