26.02.2007r.
I rok chemii	Badanie oscylatora harmonicznego

1) Ruchem harmonicznym nazywamy ruch odbywający się pod wpływem siły
F, proporcjonalnej do wychylenia x z położenia równowagi, lecz przeciwnie skierowanej:

F = - kx

gdzie: F - siła, x - wychylenie, k - stała sprężystości.

Ruchem harmonicznym tłumionym nazywamy ruch na który działa dodatkowo siła oporu ośrodka proporcjonalna do prędkości. Amplituda drgań w tym ruchu maleje w funkcji czasu.

Z drugiej zasady dynamiki Newtona możemy wyprowadzić równanie ruchu dla tłumionego oscylatora harmonicznego:

F = ma

gdzie F jest sumą siły -kx sprowadzającej drgające ciało do położenia równowagi oraz siły tłumiącej -bdx/dt. Stała b jest współczynnikiem tłumienia. Po podstawieniu do wzoru otrzymujemy:

-kx - b
= m

lub

m
+ b
+ kx = 0

rozwiązaniem tego równania jest wyrażenie:

x = Ae
cos(ωt + φ)

Okresem T w ruchu harmonicznym nazywamy czas jednego pełnego drgnięcia.

T = 2

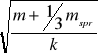
2) - obciążyć szalkę kolejno odważnikami o masie m od 0,25 kg do 3 kg i wyznaczyć dla każdego obciążenia czas trwania 20 drgań oscylatora. Masa szalki m_sz = 0,30 kg. Masa jednego odważnika + 0,25 kg.

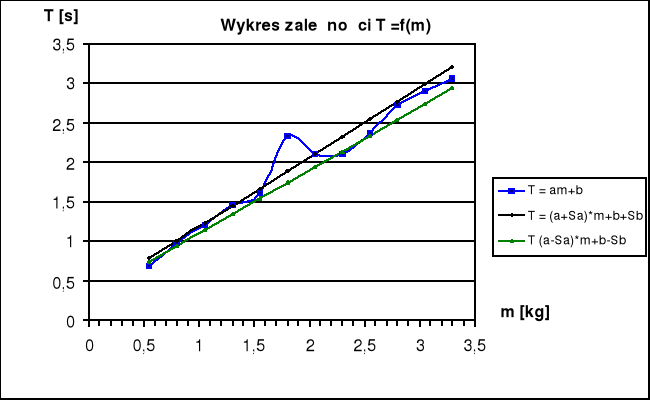
- sporządzić wykres T² = f(m). Uwzględnić masę szalki.

- na podstawie danych do wykresu, wyznaczyć metodą najmniejszych kwadratów współczynniki a i b prostej (T² = am +b)

- obliczyć masę efektywną sprężyny m_s.

- obliczyć stałą k sprężyny.

3) T² = am + b

a =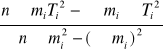

a = 0,84

a =
=> k =

k =
= 46,95

b =
)

b = 0,3

b =
=> m_s =

m_s = 1,07

4)

5. S_a =
   

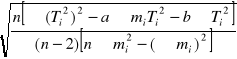
S_a = 0,038

S_b =

S_b = 0,006

---