TEORIA POPYTU
Zakupywany koszyk towarów - wartość koszyka nie może przekroczyć posiadanego dochodu.
Koszyk optymalny - daje on nam max użyteczność towaru a co za tym idzie max zadowolenie klienta.
Relacja preferencji (własności) - dwa koszyki x oraz y sa w relacji preferencji, jeżeli konsument przedkłada koszyk x nad y (koszyk towarów x jest słabo preferowany niż koszyk y, albo koszyk towarów x jest nie gorszy od koszyka towarów y).
Koszyki indyferentne. Jeżeli koszyk x jest przez konsumenta silnie preferowany nad koszyk y, wówczas mówimy, że koszyk x jest zdaniem konsumenta lepszy od koszyka y. (o indyferentności koszyka towarów mówimy także, że są dla konsumenta jednakowo dobre - są to koszyki równoważne).
Funkcja użyteczności. Każdemu koszykowi przypisujemy liczby rzeczywiste (sztuczny twór), cechy opisujące przydatność koszyka, z zachowaniem preferencji; lepszy koszyk większa preferencja - jest to funkcja ilości towaru w koszyku.
Wyraża subiektywny stosunek konsumenta do oferowanych na rynku koszyków towarów. Jest to funkcja rzeczywista określona na przestrzeni towarów. Jeżeli funkcja użyteczności związana jest z określoną relacją preferencji, to wprowadza liczbową charakterystykę tej samej, porządkowej struktury pola preferencji. Własności funkcji użyteczności: wklęsła, niedosyt. Istnienie jednej funkcji użyteczności oznacza istnienie nieprzeliczalnego zbioru takich funkcji.
Krańcowa użyteczność towaru. Jest to pochodna funkcji użyteczności, wzrost (spadek) użyteczności całego koszyka przy jednostkowym wzroście ilości towaru; wzrost ilości jakiegokolwiek towaru w koszyku przy nie zmienionych ilościach pozostałych towarów zwiększa użyteczność koszyka.
Prawo Gossena. Krańcowa użyteczność towaru maleje ze wzrostem jego spożycia, przy wzroście towaru rośnie użyteczność, ale wzrost jest coraz wolniejszy (pochodne funkcji urzyteczności są dodatnie, druga pochodna jest ujemna).
Substytucja towarów. Wymiana towarów z zachowaniem tej samej użyteczności koszyka;
Krańcowa stopnia substytucji - pokazuje o ile powinna zwiększyć j-tego towaru przy zmniejszaniu o jednostkę i-tego towaru, aby użyteczność koszyka towarów nie zmniejszyła się
Elastyczność substytucji - pokazuje o ile % powinna zwiększyć się ilość j-tego towaru przy zmniejszeniu o jednostkę ilości i-tego, aby użyteczność koszyka towarów nie zmieniła się
Zadanie maksymalizacji użyteczności. Znaleźć taki koszyk, który jest najbardziej urzyteczny, poruszmy się przy wartości dochodu jaki dysponujemy,
Funkcja popytu. Określa zapotrzebowanie i optymalny koszyk zakupów przy zadanych cenach i dochodzie.
Linia budżetowa. Wartość wyczerpania dochodu leży na linii budżetowej; o koszyku towarów mówimy, że leży na linii budżetowej, jeżeli spełnia warunek <p,x>=1
Brak iluzji pieniądza - funkcja popytu jest dodatnio jednorodna stopnia 0, tzn. Popyt konsumpcyjny zależy od stosunku cen i dochodów, a nie od ich względnego poziomu.
Dochód kompensujący zmianę ceny. Przyrost dochodu kompensuje zmianę cen, jeżeli pozwala na kupno takiego koszyka towarów, którego nabycie nie zmniejszy stopnia zadowolenia, jakie mógłby osiągnąć konsument przed zmianą ceny.
Równanie Słuckiego. Całkowity efekt wpływu zmiany ceny na wielkość popytu jest równy sumie efektu z tytułu zmiany ceny kompensowanej przez odpowiednią zmianę dochodu i wpływu, który na zmianę popytu wywiera zmiana dochodu.
Czyli prościej mówiąc efekt zmiany ceny zależy od dochodu i cen. Zmiana popytu zależy od zmiany cen, dochodu lub obu tych czynników na raz. Równanie opisuje jaki jest udział cen i dochodu w efekcie zmiany popytu
Kompensowany wzrost cen. Przy wzroście dochodu, popyt na ten towar maleje (im droższy towar, tym rzadziej się go kupuje); Zmiana popytu na i-ty towar przy kompensowanym jednostkowym wzroscie ceny j-tego towaru jest równa zmianie poputu na j-ty towar przy kompensowanym jednoskowym wzroscie ceny i-tego towaru.
Paradoks Giffena. Jeżeli wzraz ze wzrostem ceny popyt na towar rośnie, to wraz ze wzrostem dochodu popyt na ten towar maleje.
Elastyczność cenowa popytu. Pokazule o ile % zmieni sie popyt na towar przy wzroście jego ceny o 1%.
Elastyczność krzyżowa popytu. Przedstawia %-ową zmianę popytu na i-ty towar wywołaną wzrostem ceny j-tego towaru o 1%.
Elastyczność dochodu. Wskazuje o ile % zmieni sie popyt na towar przy wzroscie dochodu o 1%.
Klasyfikacja towarów:
Meridiana - średnia gdzie odrzucamy skrajne wartości a resztę uśredniamy
Zadanie maksymalizacji zysku - zasadniczym motywem dzialania producentów jest maksymalizacja dochodów. Dochody to różnica pomiędzy wartością sprzedaży a wart. nakładów. Zadanie maksymalizacji zysku w warunkach długookresowej strategii rozwoju przyjmuje postać max(p f(x)-<v,x>) przy ograniczeniu x≥0 tzn. Warunek nieujemności nakładów, gdzie p-cena towaru, x-wektor nakładów, v-wektor cen.
Strategia długookresowa. Cechą charakterystyczną p-stwa w takiej sytuacji istnieje możliwość wyboru dowolnego wektora nakładów (dostępna jest każda potrzebna w procesie produkcji ilość towarów).
Strategia krótkookresowa. P-stwa w krótkich okresach napotyka różne bariery związane z ograniczonością czynników oraz środków produkcji.
Optymalna wielkość nakładów. Do ilości nakładów dobieramy odpowiednią ilość produktów. Manipulujemy nakładami by zmniejszyć koszty.
Funkcja produkcyjnego popytu na towary. Wyjaśnia jak popyt produkcyjny na towary zależy od ceny towaru wytworzonego i cen towarów zużytych w procesie produkcji.
Funkcja podaży towaru. Ustala zależność optymalnego rozmiaru produkcji od cen towaru wytworzonego i cen towarów zużytych.
Funkcja kosztów p-stwa. Funkcja ustalająca zależność minimalnych kosztów produkcji do wielkości produkcji.
Optymalna wielkość produkcji. Optymalną dla p-stwa wlk produkcji można ustalić rozwiązując zadanie max(py-c(y)) pod warunkiem, że jakakolwiek produkcja istnieje y≥0. Tak dobieramy produkcję aby zminimalizować koszty.
Całkowita podaż towarów. Suma tego co znajduje sie na rynku - zapasy konsumenta i proces produkcyjny konsumenta.
Całkowity popyt. Tworzy suma wybranych kosztów towarów.
Globalny bilans popytu i podaży. Zapotrzebowanie nie przekracza podaży.
Indywidualny bilans dochodów i wydatków. Wydatki nie mogą przekroczyć dochodu konsumenta, czyli sumy wartości zapasów i udziałów w dochodzie producenta.
Stan równowagi konkurencyjnej. Wektor popytu, podaży i ceny tworzy stan równowagi, jeżeli:
To co produkuję przynosi maximum dochodu
Konsument nie moze zapłacić wiecej niż jest w stanie uzyskać
Istnieje taki koszyk towarów, aby zmieścić się w dochodach i być najbardziej użyteczny
Popyt nie może przekraczać podaży
Pareto-optymalność. Wektor popytu, podaży i ceny jest wektorem Pareto-optymalnym, jeżeli nie istnieje wektor popytu, podaży i ceny taki że:
Użyteczność jest większa niż optymalna
Dla co najmniej 1 konsumenta użyteczność nowego towaru jest wyraźnie znacząca
proporcjonalne zwiększenie ( zmniejszenie) nakładów prowadzi do proporcjonalnego zwiększenia ( zmniejszenia) procesu produkcji.
malejące przychody zwiększając α- krotne nakłady (α>1) nie doprowadzi to do α-krotnego zwiększenia wyników
rosnące przychody- zwiększając α- krotne nakłady [α∈(0,1)] nie doprowadzi to do ograniczenia produkcji.
krańcowa wydajność tej funkcji mówi o ile wzrośnie produkcja jeśli nakłady wzrosną o x;
elastyczność produkcji względem i-tego nakładu- jeśli i-krotnie zwiększymy nakłady to i-krotnie wzrośnie produkcja;
izokwanta prod. - zestaw wszystkich nakładów które dają ten sam poziom produkcji;
substytucja i-tego nakładu przez j-ty nakład ; dla danej ilości i-tego nakładu dobieram j-ty nakład aby produkcja była określona
krańcowa stopa subs. mówi jak zmiana ilości i-tego nakładu wpłynie na ilość j-tego nakładu;
elastyczność substytucji;jeżeli %zmienimy nakład i-ty to taka będzie zmiana j-tego nakładu
Narysuj linię budżetową dla I=100 p1=10 p2=20
Funkcja użyteczności ma postać
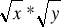
- wyznaczyć graficznie optymalny koszyk towarów wiedząc że I=100 p1=10 p2=20Funkcja kosztów przedsiębiorstwa ma postać y2 zaś cena zbytu jednostki towaru 4 wyznaczyć graficznie i numerycznie optymalną wielkość produkcji.
Funkcja produkcji ma postać
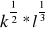
o ile należy zmniejszyć nakład pracy przy 1% zwiększeniu nakładu kapitału k by wielkość produkcji nie uległa zmianie.
TOWARY |
Normalne (wzrost ceny powoduje spadek popytu) |
Giffena (wzrost ceny powoduje wzrost popytu) |
Wyższego rzędu >0 (wzrost dochodu powoduje wzrost popytu) |
Masło |
- |
Niższego rzędu <0 (wzrost dochodu powoduje spadek popytu) |
Margaryna |
Chleb, ziemniaki Irlandia XIX w. |
TEORIA PRZEDSIĘBIORSTWA
MODELE RYNKU
Żaden konsument nie jest w stanie zwiększyć bez naruszenia globalnej równowagi koszyka, czyli konsumenci wiedzą ile kupować, ile produkować, ile maja kosztować towary aby uzyteczność i zysk były maksymalne.
TEORIA PRODUKCJI
1) Dopuszczalny proces produkcyjny - jest to para (x,y) gdzie x jest to wektor nakładów (zyżycia) : x=(x1…xk), y jest to wektor produktów (produkcji) y=(y1…yn). Mówi nam jak Y można wytworzyć z X. Takich procesów produkcyjnych może być bardzo dużo. W dopuszczalnym procesie produkcji i-ty towar może być: -równocześnie zuzywany i wytwarzany np. w elektrowni energia elektryczna, -wyłącznie zużywany np. ruda żelaza w hucie, -wyłącznie wytwarzany np. w piekarni.
Przestrzeń produkcyjna -to zbiór wszystkich (technologicznie) dopuszczalnych procesów produkcyjnych czyli to co przedsiębiorstwo może wyprodukować. Są to wszystkie nakłady przedsięb i to co można z tych nakładów wytworzyć. Z⊂R k+n
k-nakłady n-produkty
3. Przychody
4. Brak rogu obfitości - Z niczego nic nie można wytworzyć - bez nakładów nie ma wyników czyli 0 = 0.
5. Marnotrawstwo .I (marn nakładów)-Jeżeli z wektora nakładów x można otrzymać wektor produkcji y to można także otrzymać każdy wektor y'<y (mozna wyprodukować mniej) w przypadku tym są nie w pełni wykorzystane moce produkcyjne.
Marnotrawstwo II (produkcji)-jezeli z wektora nakładów x można otrzymać wektor produkcji y to tę samaprodukcję można wytworzyć nakładami x'>x (jezeli z pewnej ilości surowca mozna wyprodukować ileś produktów to z większej ilości można wyprodukować tyle samo).
6. Funkcja produkcji - pozwala ustalić max wykorzystanie nakładów przy założonych środkach.
Jest póładdytywna ∀x1,x2 f(x1+x2)>= f(x1)+f(x2). nieh k=2 ;x1=k-jest to udział kapitału, x2=l-udział pracy. Funkcja produkcji Cobba -Douglasa y= kαLβ (αβ -są to współczynniki). F P- mówi o tym ile można maksymalnie wytworzyć z x nakładów. Zależność między nakładami a wynikami.
7. Krańcowa wydajność - ilóściwy wzrost produkcji przy jednostkowym wzroście nakładów. Jest to dynamika wzrostu produkcji przy zwiększaniu nakładów.
8. Elastyczność produkcji - wzrost względny- proporcjonalne zwiększanie nakładów. Mówi o ile procent wzrośnie produkcja, gdy skala nakladow zwiększy się o 1% d ln f(x) ;d ln x
9. Izokwanta produkcji - jest to zbiór wszystkich możliwych nakładów, które dają tą samą wielkość produkcji.
10. Substytucja -jak zastepować1-sy nakład drugim nakładem aby nie zmieniać wielkości produkcji, czyli utrzymanie produkcji na tym samym poziomie przy ilościowej zmianie naklaów i-tych lub j-tych
11. Krańcowa stopa substytucji - pokazuje jjaką ilością i-tego towaru należy zastąpic jednostkowy spadek ilości i-tego towaru w wektorze nakładów x aby wielkość produkcji nie zmieniła się. (mówi jak wpłynie ilościowa zmiana nakładu i-tego na ilość towaru j-tego.)
12. Elastyczność substytucji - względna zmiana procentowa. Jeśli zmienia procentowo ilość i-tego nakladu to jak się zmieni ilość j-tego nakładu.
13. Funkcja produkcji Cobba -Douglassa, y=ax1αax2β
CES - Funk C-D ;y=KαLβ gdzia K-nakłady kapitału, L- nakład pracy. αβ-stałe parametry produkcji
Funkcja produkcji CES: y-β=aK-β+bl-β ;a-krańcowa wydajność; b- substytucja pracy przez kapitał; c- elast. substytucji
RÓWNOWAGA RYNKOWA MODEL ARROWA-HURWICZA
1. założenia modelu - model ten opisuje zachowanie się grupy ludzi przybywających z towarami na rynek z zamiarem ich sprzedaży i kupna w zamian innych potrzebnych im towarów. Uczestników tej wymiany nazywamy ogólnie handlowcami;-handlowcy nie dysponują żadnymi innymi dochodami poza tymi, które uzyskują ze sprzedaży zapasów swoich towarów;- wartość nabywanego przez handlowca koszyka towarów jest równa wartości towarów przez niego sprzedanych, czyli wszystko co zarobił to wydał.
2. Zadania handlowca - interesuje nas czy istnieją takie ceny przy których: handlowcy max. swoje korzyści;-popyt na towary jest równy ich podaży czyli każdy towar ma swojego nabywcę.
3. Funkcja popytu - nazywamy funk. uzależniającą popyt konsumenta na towary od cen towarów I dochodu konsumenta
4. Popyt nadmierny - wektorem nadniernego popytu na towary jest różnica pomiędzy popytem a podażą. Przyjmuje ona postać z(p)=Σ f(p)-Σy. Dodatnia wartość Z(p)oznacza nadwyżkę popytu nad podażą towaru, ujemna wart. sygnalizuje nadmiar podaży w stosunku do zgłaszanego popytu. F.ta spełnia następujący warunek: popyt na towar oferowany za darmo zawsze przekracza jego podaż.
5. Równowaga rynkowa - równowagę na rynku utożsamiamy z taką sytuacją, kiedy popyt na towary zostaje zrównoważony przez podaż, a każdy z uczestników wymiany opuszcza rynek w przekonaniu że przy tych cenach, które ostatecznie się ustaliły dokonał najkorzystniejszego zakupu towaru.Mówimy, że rynek jest w równowadze, jeżeli ustaliły się na nim ceny p>=0 oraz p≠0, przy których wektor nadmiernego popytu spełnia warunek z (p)=0
6. Ceny równowagi - to takie które zerują wektor nadmiernego popytu Wektor cen równowagi: wektor p>=0 oraz p≠0 taki że z(p)=0 zatem istnieje wektor cen równowagi
ZADANIA
Czyli towaru pierwszego max możnemu kupić 10 szt, towaru 2 możemy kupić max 5 szt.
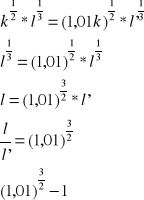
O tyle powinno się zmniejszyć l ⇑
Praca pochodzi z serwisu www.e-sciagi.pl
Wyszukiwarka