Oznaczenia

R(t) − funkcja niezawodności,

F(t) − funkcja zawodności,

ET − oczekiwany czas zdatności,

f(t) − gęstość prawdopodobieństwa uszkodzeń,

λ(t) − intensywność uszkodzeń,

μ(t) − intensywność odnowy.

Indeks dolny „e” odnosi się do pojedynczego elementu, indeks dolny „u” do całego urządzenia, zaś indeksy dolne „A” lub „B” do poszczególnych struktur, przy strukturach niezawodnościowych złożonych.

Wzory ogólne

,
,

Rozkład wykładniczy czasu zdatności elementu

λ − intensywność uszkodzeń elementu

Dla elementu:
,
,

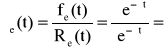
− dla rozkładu wykładniczego intensywność uszkodzeń elementu jest stała

− oczekiwany czas zdatności elementu,

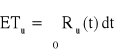
− oczekiwany czas zdatności urządzenia,

Rozkład jednostajny czasu zdatności elementu

k − kres górny czasu zdatności elementu

Dla elementu:
,
,

− dla rozkładu jednostajnego gęstość prawdopodobieństwa uszkodzenia elementu jest stała

− oczekiwany czas zdatności elementu,

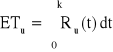
− oczekiwany czas zdatności urządzenia,

Struktury niezawodnościowe

− szeregowa

Funkcja niezawodności takiej struktury jest iloczynem funkcji niezawodności poszczególnych elementów:

Intensywność uszkodzeń takiej struktury jest równa sumie intensywności uszkodzeń poszczególnych elementów:

− równoległa

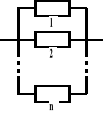
Funkcja zawodności takiej struktury jest iloczynem funkcji zawodności poszczególnych elementów:

Rezerwa nieobciążona

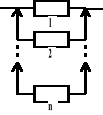
Oczekiwany czas zdatności takiego układu jest równy sumie oczekiwanych czasów zdatności poszczególnych elementów:

Rezerwa obciążona (zwykłe równoległe połączenie)

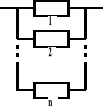
Tu oczekiwany czas zdatności urządzenia liczymy wg wzoru całkowego. Pozostałe parametry [f_u(t), λ_u(t)] liczymy z podstawowych wzorów.

Używane w zadaniach całki i pochodne

,
,
,

Zadanie 1 (było na egzaminie)

Urządzenie składa się z dwóch elementów. Uszkodzenie jednego z elementów powoduje uszkodzenie urządzenia. Intensywności uszkodzeń elementów nie zależą od czasu, a ich wartości nie są znane. Intensywność uszkodzeń pierwszego elementu jest dwa razy większa od intensywności uszkodzeń elementu drugiego. Oczekiwany czas zdatności urządzenia jest znany, a jego wartość jest równa 66 [h] 40 [min.]. Obliczyć oczekiwane czasy zdatności elementów.

λ_u = λ₁ + λ₂, λ₁ = 2λ₂ → λ_u = 3λ₂

→
→
→
,

λ₁ = 2λ₂ →
,

Odp. ET₁ = 100 [h], ET₂ = 200 [h].

Zadanie 2 (było na egzaminie)

Urządzenie o strukturze szeregowej składa się z dwóch elementów. Intensywności uszkodzeń elementów są stałe. Obliczyć intensywności uszkodzeń elementów, jeżeli oczekiwany czas zdatności elementu drugiego jest dwa razy większy od oczekiwanego czasu zdatności elementu pierwszego. Oczekiwany czas zdatności urządzenia jest równy 300 [h].

λ_u = λ₁ + λ₂,
,
→

ET₂ = 2ET₁ →
→

→
→
→ ET₁ = 450 [h]

→
, ET₂ = 2ET₁ → ET₂ = 900 [h],
→

Odp.
,

Zadanie 3 (było na egzaminie)

Urządzenia składa się z trzech elementów. Uszkodzenie jednego z elementów powoduje uszkodzenie urządzenia. Intensywności uszkodzeń elementów nie zależą od czasu. Intensywność uszkodzeń drugiego elementu jest trzy razy większa od intensywności uszkodzeń elementu pierwszego, a intensywność uszkodzeń elementu trzeciego jest dwa razy większa od intensywności uszkodzeń elementu drugiego. Oczekiwany czas zdatności urządzenia jest równy 10 [h]. Obliczyć oczekiwane czasy zdatności elementów.

λ_u = λ₁ + λ₂ + λ₃, λ₂ = 3λ₁, λ₃ = 2λ₂ → λ₃ = 6λ₁ → λ_u = λ₁ + 3λ₁ + 6λ₁ = 10λ₁

→
→
→
,

λ₂ = 3λ₁ →
,

λ₃ = 6λ₁ →
,

Odp. ET₁ = 100 [h], ET₂ = 33 [h] 20 [min.], ET₃ = 16 [h] 40 [min.].

Zadanie 4 (było na egzaminie)

Urządzenie o strukturze szeregowej składa się z jednakowych elementów, których intensywności uszkodzeń nie zależą od czasu. Z ilu elementów składa się to urządzenie, jeżeli oczekiwany czas zdatności elementu jest równy 10 [h], a intensywność uszkodzeń urządzenia jest równa 0,001 [1/h].

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ_u = 0,001 [1/h], ET_e = 10 [h]

Szukane: n = ? (ilość elementów, z których składa się dana struktura niezawodnościowa)

λ_u = λ_e + λ_e + … + λ_e = n⋅λ_e

→
→ n = λ_u⋅ET_e = 100

Odp. Urządzenie składa się z 100 elementów.

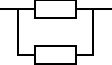
Zadanie 5 (było na egzaminie)

Urządzenie składa się z dwóch jednakowych elementów, elementu podstawowego i elementu rezerwowego będącego rezerwą obciążoną. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest równy
120 [h]. Wyznaczyć przedział czasu, w którym gęstość prawdopodobieństwa uszkodzeń urządzenia jest większa od gęstości prawdopodobieństwa uszkodzeń elementu.

,
, k = ?, R_u(t) = ?

→
→ k = 240 [h]

,
→

→
,
→

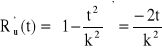
f_u(t) > f_e(t) →
→
→

Odp. t ∈ (120h, 240h>.

Zadanie 6 (z wykładów)

Urządzenia o strukturze niezawodnościowej jak na rysunku składa się z czterech jednakowych elementów. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest równy 150 [h]. Wyznaczyć przedział czasu, w którym intensywność uszkodzeń urządzenia jest mniejsza od intensywności uszkodzeń elementu.

,
,
→

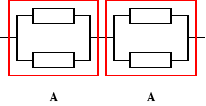
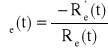
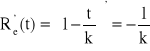
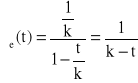
λ_u(t) = λ_A(t) + λ_A(t) = 2λ_A(t),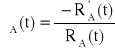
, R_A(t) = ?

,
,
→

,
,
→

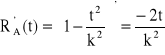
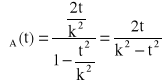
λ_u(t) < λ_e(t) →
→
→

→
→

→
→ k = 300 [h] →

Odp. t ∈ <0, 100h).

Zadanie 7 (było na egzaminie)

Urządzenie o strukturze szeregowej składa się z dwóch jednakowych elementów. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym zero. Oczekiwany czas zdatności elementu jest równy 120 [h]. Wyznaczyć przedział czasu, w którym gęstość prawdopodobieństwa uszkodzeń urządzenia jest większa od gęstości prawdopodobieństwa uszkodzeń elementu.

,
, k = ?, R_u(t) = ?

→
→ k = 240 [h]

,
→

→

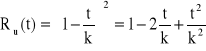
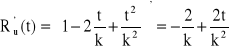
f_u(t) > f_e(t) →
→
→
→

Odp. t ∈ <0, 120h).

Zadanie 8 (było na egzaminie)

Urządzenia o strukturze niezawodnościowej jak na rysunku składa się z czterech jednakowych elementów. Czas zdatności elementu ma rozkład wykładniczy o wartości oczekiwanej równej 100 [h]. Wyznaczyć intensywność uszkodzeń tego urządzenia.

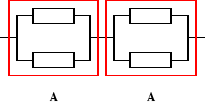
λ_u(t) = λ_A(t) + λ_A(t) = 2λ_A(t),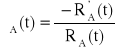
, R_A(t) = ?

,
,

→

→

→

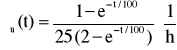
Odp: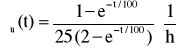
.

Zadanie 9 (było na egzaminie)

Urządzenie składa się z trzech jednakowych elementów, elementu podstawowego i dwóch elementów rezerwowych będących rezerwą nieobciążoną. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Gęstość prawdopodobieństwa uszkodzeń elementu jest równa 0,001 [1/h]. Wyznaczyć oczekiwany czas zdatności urządzenia.

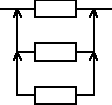
ET_u = ET_e + ET_e + ET_e = 3ET_e,
→
, k = ?

→
→ k = 1000 [h],

Odp. ET_u = 1500 [h].

Zadanie 10 (było na egzaminie)

Urządzenie składa się z trzech jednakowych elementów, elementu podstawowego i dwóch elementów rezerwowych będących rezerwą nieobciążoną. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności urządzenia jest równy 1500 [h]. Wyznaczyć gęstość prawdopodobieństwa uszkodzeń elementu.

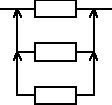
, k = ?

ET_u = ET_e + ET_e + ET_e = 3ET_e,
→

→ k = 1000 [h] →

Odp.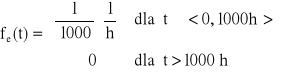
.

Zadanie 11 (było na egzaminie)

Urządzenie składa się z trzech jednakowych elementów, elementu podstawowego i dwóch elementów rezerwowych będących rezerwą nieobciążoną. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Gęstość prawdopodobieństwa uszkodzeń elementu jest równa 0,001 [1/h]. Wyznaczyć maksymalny czas zdatności urządzenia.

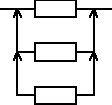
T_maxu = T_maxe + T_maxe + T_maxe = 3T_maxe, T_maxe − maksymalny czas zdatności elementu

T_maxe = k → T_maxu = 3k, k = ?,
→
→ k = 1000 [h]

T_maxu = 3000 [h]

Odp. Maksymalny czas zdatności urządzenia jest równy 3000 [h].

Zadanie 12 (było na egzaminie)

Urządzenie składa się z trzech jednakowych elementów, elementu podstawowego i dwóch elementów rezerwowych będących rezerwą nieobciążoną. Czas zdatności elementu ma rozkład wykładniczy z parametrem λ równym 0,005 [1/h]. Wyznaczyć oczekiwany czas zdatności urządzenia.

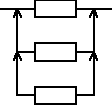
ET_u = ET_e + ET_e + ET_e = 3ET_e

→

Odp. ET_u = 600 [h].

Zadanie 13

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z jednakowych elementów. Oczekiwany czas zdatności elementu jest równy 120 [h]. Obliczyć oczekiwany czas zdatności urządzenia, jeżeli intensywność uszkodzeń elementu jest stała.

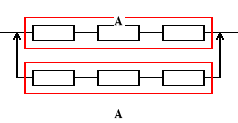
ET_u = ET_A + ET_A = 2ET_A, ET_A = ?

, λ_A = λ + λ + λ = 3λ →
, λ = ?

→
→ ET_A = 40 [h] → ET_u = 80 [h]

Odp. ET_u = 80 [h].

Zadanie 14 (było na egzaminie)

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z czterech elementów. Czas zdatności elementów ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu 1 jest równy 900 [h], a czas zdatności elementu 2 jest równy 600 [h]. Obliczyć oczekiwany czas zdatności urządzenia.

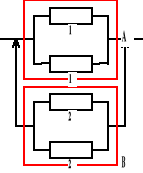
ET_u = ET_A + ET_B, ET_A = ?, ET_B = ?

Wyznaczam oczekiwany czas zdatności dla urządzenia o strukturze równoległej, składającej się z dwóch jednakowych elementów:

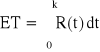
, R(t) = ?

,
,
→
→

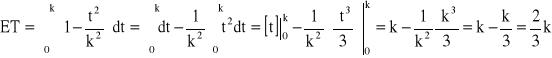
Dla struktury A:
, k₁ − kres górny czasu zdatności elementu 1

→
→ k₁ = 1800 [h] →

Dla struktury B:
, k₂ − kres górny czasu zdatności elementu 2

→
→ k₂ = 1200 [h] →

ET_u = 1200 + 800 = 2000 [h]

Odp. ET_u = 2000 [h].

Zadanie 15 (z wykładów)

Urządzenia o strukturze niezawodnościowej jak na rysunku składa się z trzech jednakowych elementów. Intensywność uszkodzeń elementu jest stała i równa 0,001 [1/h]. Wyznaczyć intensywność uszkodzeń urządzenia, a następnie obliczyć jej wartość w chwili 0.

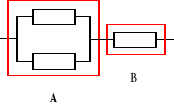
λ_u(t) = λ_A(t) + λ_B(t)

λ_B(t) = λ = 0,001 [1/h],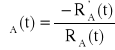
, R_A(t) = ?

,
,

→

Odp.
,
.

Zadanie 16 (było na egzaminie)

Urządzenie składa się z trzech jednakowych elementów, elementu podstawowego i dwóch elementów rezerwowych będących rezerwą obciążoną. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest równy 100 [h]. Wyznaczyć gęstość prawdopodobieństwa uszkodzeń tego urządzenia.

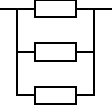
, R_u(t) = ?

,
,
→

→
→

→
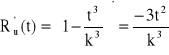
→ k = 200 [h] →

Odp.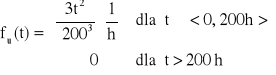
.

Zadanie 17 (było na egzaminie)

O ile różnią się oczekiwane czasy zdatności dwóch urządzeń zbudowanych z dwóch jednakowych elementów. Pierwsze ma równoległą, a drugie szeregową strukturę. Czas zdatności elementu ma rozkład wykładniczy. Oczekiwany czas zdatności elementu jest równy 120 [h].

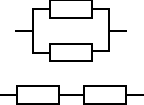
Dla struktury równoległej: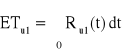
, R_u1(t) = ?

,
,

→

→
→
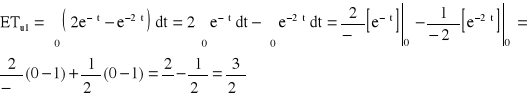
→ ET_u1 = 180 [h]

Dla struktury szeregowej:
, λ_u2 = λ + λ = 2λ →

→ ET_u2 = 60 [h], czyli ET_u1 = 3ET_u2

Odp. Oczekiwany czas zdatności dla struktury równoległej jest 3 razy większy.

Zadanie 18

O ile różnią się oczekiwane czasy zdatności dwóch urządzeń zbudowanych z dwóch jednakowych elementów. Pierwsze ma równoległą, a drugie szeregową strukturę. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest równy 120 [h].

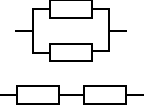
Dla struktury równoległej: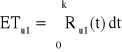
, R_u1(t) = ?

,
,
→
→

→
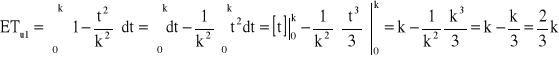
→ k = 240 [h] → ET_u1 = 160 [h]

Dla struktury szeregowej: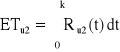
, R_u2(t) = ?

,
→

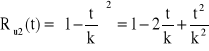
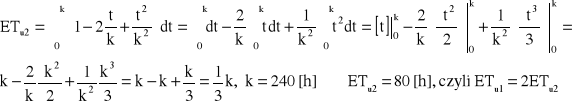
Odp. Oczekiwany czas zdatności dla struktury równoległej jest 2 razy większy.

Zadanie 19 (było na egzaminie)

Urządzenia o strukturze niezawodnościowej jak na rysunku składa się z czterech jednakowych elementów. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym 0. Oczekiwany czas zdatności elementu jest równy 100 [h]. Obliczyć intensywność uszkodzeń tego urządzenia w chwili równej oczekiwanemu czasowi zdatności elementu.

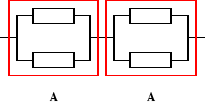
λ_u(t) = λ_A(t) + λ_A(t) = 2λ_A(t),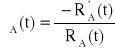
, R_A(t) = ?

,
,
→

,
,
→

→
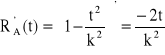
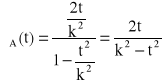
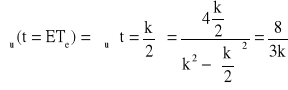
→ k = 200 [h] →

Odp.
.

Zadanie 20

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z czterech jednakowych elementów. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym zero. Obliczyć stosunek oczekiwanego czasu zdatności elementu do oczekiwanego czasu zdatności urządzenia.

,
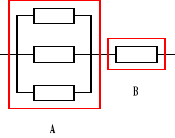
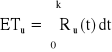
, R_u(t) = ?

,
,

,
,
→
→

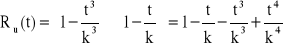
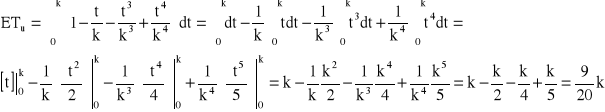
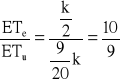
Odp.
.

Zadanie 21 (było na egzaminie)

Urządzenie o strukturze równoległej składa się z dwóch jednakowych elementów. Który rozkład czasu zdatności, jednostajny czy wykładniczy, będzie korzystniejszy z punktu widzenia niezawodności rozpatrywanego urządzenia. Oczekiwany czas zdatności elementu jest równy 60 [h].

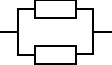
Dla rozkładu jednostajnego: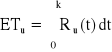
, R_u(t) = ?

,
,
→
→

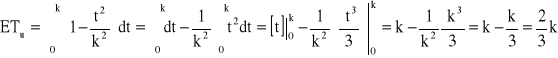
, k = ?

→
→ k = 120 [h] → ET_u = 80 [h]

Dla rozkładu wykładniczego: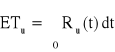
, R_u (t) = ?

,
,

→

,
→
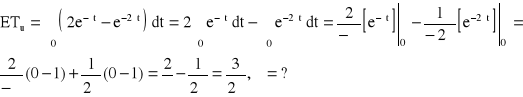
→ ET_u = 90 [h]

Jak powyżej wykazano oczekiwany czas zdatności dla rozkładu wykładniczego jest większy, wobec tego ten rozkład czasu zdatności jest korzystniejszy z punktu widzenia niezawodności rozpatrywanego urządzenia.

Zadanie 22

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z jednakowych elementów. Czas zdatności elementu ma rozkład jednostajny o kresie dolnym równym zero. Oczekiwany czas zdatności urządzenia jest równy 700 [h]. Obliczyć oczekiwany czas zdatności elementu.

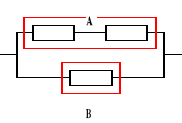
, k = ?,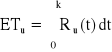
, R_u(t) = ?,
,

,
,
,

,
→

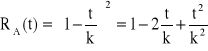
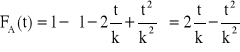
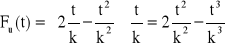
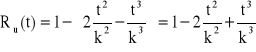
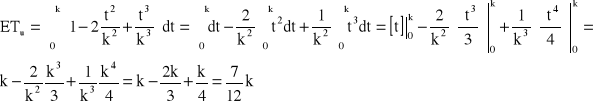
→ k = 1200 [h] → ET_e = 600 [h]

Odp. ET_e = 600 [h].

Zadanie 23 (było na egzaminie)

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z trzech elementów, których intensywności uszkodzeń nie zależą od czasu, a ich wartości nie są znane. Intensywność uszkodzeń pierwszego elementu jest dwa razy większa od intensywności uszkodzeń elementu drugiego. Oczekiwany czas zdatności urządzenia jest równy 700 [h]. Obliczyć oczekiwane czasy zdatności elementów 1 i 2.

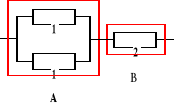
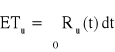
, R_u(t) = ?

,

,
,

→

, λ₁ = 2λ₂ →

→
,
,
,

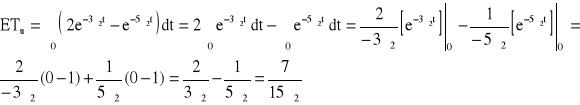
Odp. ET₁ = 750 [h], ET₂ = 1500 [h].

Zadanie 24 (było na egzaminie)

Urządzenie o strukturze niezawodnościowej jak na rysunku składa się z czterech elementów, których intensywności uszkodzeń nie zależą od czasu, a ich wartości nie są znane. Oczekiwany czas zdatności urządzenia jest równy 500 [h]. Obliczyć oczekiwane czasy zdatności elementów wiedząc, że intensywność uszkodzeń pierwszego elementu jest dwa razy większa od intensywności uszkodzeń elementu drugiego.

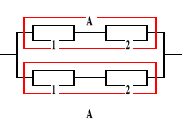
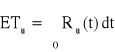
, R_u(t) = ?

,

,
,
,

λ₁ = 2λ₂ →
→

,

→
,
,
,

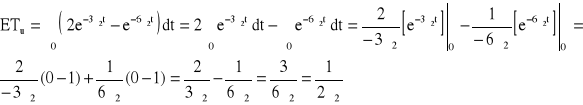
Odp. ET₁ = 500 [h], ET₂ = 1000 [h].

Zadanie 25 (było na egzaminie)

Czas zdatności pewnego obiektu ma rozkład jednostajny o kresie dolnym równym 0, a kres górny nie jest znany. Wiadomo, że oczekiwany czas zdatności obiektu jest równy 5 [lat]. Obliczyć prawdopodobieństwo tego, że rozpatrywany obiekt:

a) uszkodzi się w czwartym roku użytkowania,

b) bezawaryjnie przepracował trzy lata, uszkodzi się w czwartym roku pracy.

→
→ k = 10 lat − kres górny czasu zdatności obiektu

T − zmienna losowa czasu pracy obiektu do powstania uszkodzenia

a)
,
,
,
→

b)
,
(punkt a)

→
.

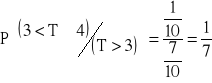
Zadanie 26

Czas zdatności obiektu ma rozkład jednostajny, którego kres dolny jest równy zero, kres górny jest równy 10 [lat]. Obliczyć prawdopodobieństwo tego, że rozpatrywany obiekt:

a) uszkodzi się w trzecim lub czwartym roku użytkowania,

b) uszkodzi się w dziesiątym roku użytkowania, jeśli wiadomo, że bezawaryjnie przepracował dziewięć lat.

k = 10 lat − kres górny czasu zdatności obiektu

T − zmienna losowa czasu pracy obiektu do chwili powstania uszkodzenia

a)
,
,
,
→

b)

,
,
→

.

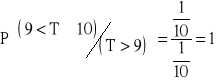
Zadanie 27 (było na egzaminie)

Urządzenie składa się z dwóch jednakowych elementów, elementu podstawowego i elementu rezerwowego będącego rezerwą obciążoną. Intensywności uszkodzeń elementów są stałe i równe 0,01 [1/h]. Intensywności odnowy również są stałe i równe 0,1 [1/h]. Obliczyć stacjonarne prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne. Pomijamy tzw. uszkodzenie o wspólnej przyczynie oraz zakładamy, że nie ma żadnych ograniczeń, co do liczby elementów, które mogą być odnawiane w tym samym czasie.

Rozpatrywane stany urządzenia:

0 - wszystkie elementy zdatne

1 - jeden element niezdatny

2 - dwa elementy niezdatne

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2

Szukane jest P₂

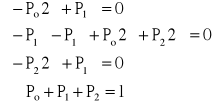
Z drugiego równania możemy zrezygnować (mamy 4 równania i 3 niewiadome)

Z pierwszego równania:

Z trzeciego równania:
, czyli:
i podstawiamy P_o i P₁ do ostatniego równania:

→
→

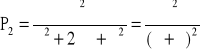
Podstawiając dane liczbowe:
,
otrzymujemy:

Odp. Prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne jest równe
.

Zadanie 28 (było na egzaminie)

Urządzenie składa się z dwóch jednakowych elementów, elementu podstawowego i elementu rezerwowego będącego rezerwą nieobciążoną. Intensywności uszkodzeń elementów są stałe i równe 0,01 [1/h]. Intensywności odnowy również są stałe i równe 0,1 [1/h]. Pomijamy tzw. uszkodzenie o wspólnej przyczynie. Uszkodzone elementy są odnawiane kolejno. Obliczyć stacjonarne prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne.

Rozpatrywane stany urządzenia:

0 - wszystkie elementy zdatne

1 - jeden element niezdatny

2 - dwa elementy niezdatne

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2

Szukane jest P₂

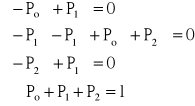
Z drugiego równania możemy zrezygnować (mamy 4 równania i 3 niewiadome)

Z pierwszego równania:

Z trzeciego równania:
, czyli:
i podstawiamy P_o i P₁ do ostatniego równania:

→
→

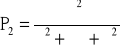
Podstawiając dane liczbowe:
,
otrzymujemy:

Odp. Prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne jest równe
.

Zadanie 29

Urządzenie składa się z dwóch jednakowych elementów. Uszkodzenie jednego z elementów powoduje uszkodzenie urządzenia. Intensywności uszkodzeń elementów są stałe i równe 0,01 [1/h]. Intensywności odnowy również są stałe i równe 0,1 [1/h]. Obliczyć stacjonarne prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne. Zakładamy, że element może ulec zniszczeniu wtedy, gdy urządzenie działa oraz, że nie rozpatrujemy tzw. uszkodzenia o wspólnej przyczynie.

Rozpatrywane stany urządzenia:

0 - urządzenie zdatne,

1 - urządzenie niezdatne

P_o, P₁ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1

Szukane jest P₁

,
→

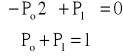
Podstawiając dane liczbowe:
,
otrzymujemy:
.

Odp. Prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne jest równe
.

Zadanie 30

Urządzenie o szeregowej strukturze niezawodnościowej składa się z trzech jednakowych elementów. Intensywność uszkodzeń elementu jest równa λ, a intensywność odnowy jest równa μ. W przypadku wystąpienia uszkodzenia o wspólnej przyczynie uszkodzenie urządzenia następuje z intensywnością λ_w. Odnowienie tak uszkodzonego urządzenia następuje z intensywnością odnowy μ_w. Obliczyć stacjonarny współczynnik gotowości tego urządzenia.

Rozpatrywane stany urządzenia:

0 - wszystkie elementy zdatne,

1 - jeden element niezdatny,

3 - trzy elementy niezdatne

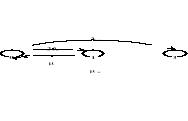
P_o, P₁, P₃ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 3

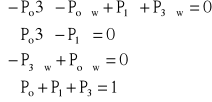
Z pierwszego równania możemy zrezygnować (mamy 4 równania i 3 niewiadome)

Współczynnik gotowości − k_g = P_o

Z drugiego równania:
, z trzeciego równania:

→

Odp.
.

Zadanie 31

Urządzenie składa się z dwóch jednakowych elementów, elementu podstawowego i elementu rezerwowego. Element rezerwowy jest rezerwą obciążoną. Intensywność uszkodzeń elementu jest równa 0,001 [1/h]. Po wystąpieniu uszkodzenia dowolnego elementu urządzenie jest nadal zdatne, ale intensywność uszkodzeń działającego elementu wzrasta o 1,5. Do odnowy uszkodzonych elementów przystępuje się, gdy urządzenie jako całość przechodzi w stan niezdatności. Intensywność odnowy całego urządzenia jest równa 0,1 [1/h]. W trakcie odnowy usuwa się wszystkie uszkodzenia. Uszkodzenia o wspólnej przyczynie pomijamy. Obliczyć stacjonarne prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne.

Rozpatrywane stany urządzenia:

0 - wszystkie elementy zdatne

1 - jeden element niezdatny

2 - dwa elementy niezdatne

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2, szukamy P₂.

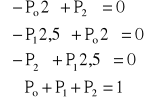
z jednego równania możemy zrezygnować (mamy 4 równania i 3 niewiadome)

z pierwszego równania:
, z trzeciego równania:

i podstawiamy do ostatniego równania otrzymując:

po przekształceniach otrzymujemy:

podstawiając dane liczbowe:
,
otrzymujemy:
.

Odp. Stacjonarne prawdopodobieństwo tego, że rozpatrywane urządzenie jest niezdatne jest równe
.

Zadanie 32 (zadanie ze skryptu mgra inż. T. Rutkowskiego)

Urządzenie składa się z elementu podstawowego i jednego elementu rezerwowego. Intensywność uszkodzeń elementu jest równa λ₁, w gdy element pracuje i λ₂ gdy jest w rezerwie. Uszkodzone elementy są odnawiane kolejno, a intensywność odnowy elementu jest równa μ. Pomijając uszkodzenie o wspólnej przyczynie obliczyć stacjonarny współczynnik gotowości tego urządzenia, gdy element rezerwowy będzie rezerwą:

a) częściowo obciążoną

b) obciążoną

c) nieobciążoną

Rozpatrywane stany urządzenia:

0 - wszystkie elementy zdatne

1 - jeden element niezdatny

2 - dwa elementy niezdatne

a)

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2

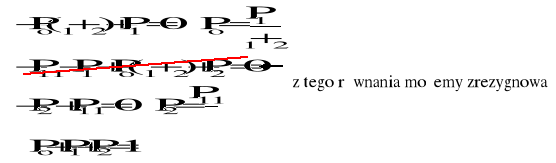
Podstawiając do ostatniego równania wyliczone wartości P_o i P₂ otrzymujemy:

→

→

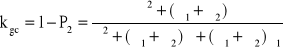
b) w tym przypadku λ₂ = λ₁

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2

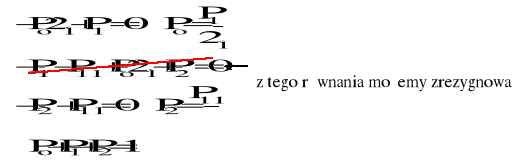
Podstawiając do ostatniego równania wyliczone wartości P_o i P₂ otrzymujemy:

→
,

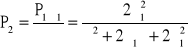
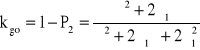
c) w tym przypadku λ₂ = 0

P_o, P₁, P₂ − stacjonarne prawdopodobieństwa, że urządzenie znajduje się odpowiednio w stanie 0, 1, 2

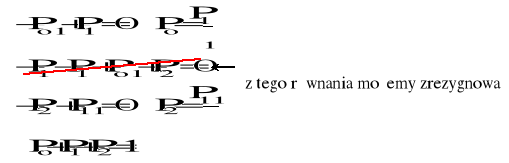
Podstawiając do ostatniego równania wyliczone wartości P_o i P₂ otrzymujemy:

,
→
.

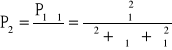
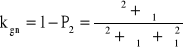
Rozkład czasu zdatności elementu − wykładniczy

Dane: λ₁ = 2λ₂, ET_u = 66 [h] 40 [min.]

Szukane: ET₁ = ?, ET₂ = ?

Rezerwa obciążona

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 120 [h]

Szukane: przedział czasu, dla którego f_u(t) > f_e(t)

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 120 [h]

Porównać oczekiwane czasy zdatności obu struktur

Rozkład czasu zdatności elementu − wykładniczy

Dane: ET_e = 120 [h]

Porównać oczekiwane czasy zdatności obu struktur

Rezerwa obciążona

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 100 [h]

Szukane: f_u(t) = ?

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 100 [h]

Szukane: λ_u(t = ET_e) = ?

Rozkład czasu zdatności elementu − jednostajny

Szukane:

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ₁ = 2λ₂, ET_u = 700 [h]

Szukane: ET₁ = ?, ET₂ = ?

Rezerwa nieobciążona

Rozkład czasu zdatności elementu −

wykładniczy

Dane: ET_e = 120 [h]

Szukane: ET_u = ?

Rezerwa nieobciążona

Rozkład czasu zdatności elementu − wykładniczy z parametrem λ

Dane: λ = 0,005 [1/h]

Szukane: ET_u = ?

Rezerwa nieobciążona

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_u = 1500 [h]

Szukane: f_e(t) = ?

Rezerwa nieobciążona

Rozkład czasu zdatności elementu − jednostajny

Dane:

Szukane: ET_u = ?

Rezerwa nieobciążona

Rozkład czasu zdatności elementu − jednostajny

Dane:

Szukane: T_maxu = ? (maksymalny czas zdatności urządzenia)

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ₁ = 2λ₂, ET_u = 500 [h]

Szukane: ET₁ = ?, ET₂ = ?

Rozkład czasu zdatności elementu − wykładniczy

Dane: ET₂ = 2ET₁, ET_u = 300 [h]

Szukane: λ₁ = ?, λ₂ = ?

Rezerwa nieobciążona

Rozkład czasu zdatności − jednostajny

Dane: ET₁ = 900 [h], ET₂ = 600 [h]

Szukane: ET_u = ?

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 120 [h]

Szukane: przedział czasu, dla którego f_u(t) > f_e(t)

Rozkład czasu zdatności elementu − wykładniczy

Dane: ET_e = 100 [h]

Szukane: λ_u(t) = ?

Dane: ET_e = 60 [h]

Porównać oczekiwane czasy zdatności urządzenia dla jednostajnego i wykładniczego rozkładu czasu zdatności elementu

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ = 0,001 [1/h]

Szukane: λ_u(t) = ?, λ_u(t = 0) = ?

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_e = 150 [h]

Szukane: przedział czasu, dla którego λ_u(t) < λ_e(t)

Rozkład czasu zdatności elementu − wykładniczy

Dane: λ₂ = 3λ₁, λ₃ = 2λ₂, ET_u = 10 [h]

Szukane: ET₁ = ?, ET₂ = ?, ET₃ = ?

Rozkład czasu zdatności elementu − jednostajny

Dane: ET_u = 700 [h]

Szukane: ET_e = ?

---