Tabela

200					Wydział Elektryczny	Semestr II	Grupa E-1

Temat: Wyznaczanie bariery potencjału na złączu PN

Dioda p-n jest jednym z najpowszechniej stosowanych elementów elektronicznych. Ze względu na asymetryczną charakterystykę prądowo-napięciową najczęściej stosuje się diodę jako element prostowniczy. Diodę stanowią dwa zetknięte ze sobą półprzewodniki, z których jeden jest typu p, a drugi typu n. Na rysunku 200.1 przedstawiony jest schemat energetyczny obu rodzajów półprzewodników.

Gdy oba półprzewodniki doprowadzimy do ścisłego kontaktu, następuje przepływ elektronów do części p oraz dziur do części n w wyniku procesu termoemisji. Ta wymiana nośników ustaje, gdy ustanie gdy wyrównają się poziomy Fermiego i między obu częściami diody wytworzy się różnica potencjałów ϕ . Schemat energetyczny diody przedstawia rys.200.2. Obszarem złącza jest obszar gdzie, pasma nie są płaskie, i w którym koncentracja elektronów jest mniejsza niż w części n, a dziur - mniejsza niż w części p. Na rysunku zaznaczono koncentrację nośników w obu obszarach - N oznacza koncentrację elektronów, P - koncentrację dziur, a indeksy n i p wskazują, do którego obszaru dana koncentracja się odnosi. Widoczne jest że w obszarze złącza jest mało nośników, więc obszar ten stanowi utrudnienie dla przepływu prądu. Miarą tego utrudnienia jest różnica potencjałów na złączu. Zwróćmy uwagę, że złącze stanowi barierę zarówno dla elektronów poruszających się w prawo, jak i dla dziur poruszających się w lewo, ponieważ energia elektronów rośnie do góry, natomiast dziur (ładunków dodatnich ) wzrasta w kierunku dołu. Zatem dla rodzajów obu nośników przejście przez złącze związane jest z wykonaniem pracy eϕ.

Przedstawiona sytuacja dotyczy nośników większościowych, tzn. elektronów z obszaru n i dziur z obszaru p. Natomiast dla nośników mniejszościowych, czyli elektronów z obszaru p i dziur z obszaru n, bariera nie stanowi przeszkody, ponieważ ich ruch odbywa się w kierunku mniejszej energii (elektrony w lewo dziury w prawo ). Bariera potencjału na złączu może być zwiększona lub zmniejszona przez przyłożenie do diody napięcia V ze źródła zewnętrznego. Wynosi ona wtedy

(200.1)

gdzie znak „+” odnosi się do przypadku, gdy do części jest przyłożony biegun ujemny źródła - mówimy wtedy, że dioda jest spolaryzowana zaporowo. W przeciwnym przypadku mówimy o polaryzacji diody w kierunku przewodzenia.

W diodzie p-n występują dwie przyczyny ukierunkowanego ruchu nośników:

1) dążenie do znaleźnienia się w obszarze najniższej energii potencjalnej oraz

2) dążenie do wyrównania koncentracji, czyli dyfuzji nośników

Mechanizm pierwszej powoduje ruch elektronów z obszaru p do obszaru n oraz dziur z obszaru n do obszaru p. Suma tych nośników tworzy prąd nasycenia I_s

(200.2)

który zależy od koncentracji N_p i P_n nośników mniejszościowych, a nie zależy od przyłożonego napięcia.

Koncentracja nośników zależy wykładniczo od położenia pasma względem poziomu Fermiego E_F . Jak wynika z rysunku 200.2, różnica energii między pasmem przewodnictwa części p i poziomem Fermiego E_F wynosi (E_W - E_F ) + eϕ . Koncentracja elektronów określona jest wzorem

(200.3)

gdzie N_C jest w przybliżeniu wielkością stałą, zwaną efektywną wielkością stanów.

Gdy złącze jest symetryczne, koncentracja dziur P_n ma taką samą wartość, tzn. P_n = N_p .

Proporcjonalność natężenia prądu nasycenia do koncentracji nośników mniejszościowych możemy zatem wyrazić równaniem

(200.4)

w którym stała C zawiera efektywną gęstość stanów, ruchliwość nośników oraz powierzchnię złącza.

Dyfuzja w złączu p-n polega na takim ruchu nośników, który prowadzi do zmniejszenia różnicy koncentracji zarówno elektronów jak i dziur po obu stronach złącza. Prąd związany z tym ruchem nazywa się prądem dyfuzji I_d i składa się z prądu elektronowego i dziurowego

(200.5)

Prąd dyfuzji ma kierunek przeciwny do kierunku prądu nasycenia, stąd wypadkowy prąd płynący przez złącze p-n jest różnicą obu prądów

, (200.6)

Prąd dyfuzji elektronów jest proporcjonalny do różnicy koncentracji elektronów, czyli do (N_n - N_p) oraz do prawdopodobieństwa pokonania bariery potencjału P_ϕ .

(200.7)

Pomiary i obliczenia

Dokładność pomiarów:

T = ± 1^oC

U = ± 1 mV

I = ± 1 μA

Tabela pomiarowa:

Tabela pomiarowa wraz z obliczonym ln I
	T = 1oC	T = 27oC	T = 46 oC
Lp.	U	I	ln I	U	I	ln I	U	I	ln I
	[mV]	[μA]	-	[mV]	[μA]	-	[mV]	[μA]	-
1	295	100	-9.21	269	100	-9.21	251	100	-9.21
2	283	95	-9.26	258	95	-9.26	241	95	-9.26
3	272	90	-9.32	248	90	-9.32	232	90	-9.32
4	260	85	-9.37	238	85	-9.37	222	85	-9.37
5	249	80	-9.43	227	80	-9.43	213	80	-9.43
6	237	75	-9.50	216	75	-9.50	200	75	-9.50
7	225	70	-9.57	203	70	-9.57	190	70	-9.57
8	211	65	-9.64	192	65	-9.64	179	65	-9.64
9	199	60	-9.72	181	60	-9.72	168	60	-9.72
10	186	55	-9.81	167	55	-9.81	156	55	-9.81
11	172	50	-9.90	156	50	-9.90	144	50	-9.90
12	157	45	-10.01	141	45	-10.01	131	45	-10.01
13	143	40	-10.13	129	40	-10.13	119	40	-10.13
14	126	35	-10.26	114	35	-10.26	105	35	-10.26
15	111	30	-10.41	99	30	-10.41	92	30	-10.41
16	95	25	-10.60	84	25	-10.60	78	25	-10.60
17	77	20	-10.82	68	20	-10.82	65	20	-10.82
18	59	15	-11.11	52	15	-11.11	48	15	-11.11
19	42	10	-11.51	35	10	-11.51	33	10	-11.51
20	21	5	-12.21	18	5	-12.21	19	5	-12.21
21	0	0	-	0	0	-	0	0	-

Wykresy ln I = f (U)

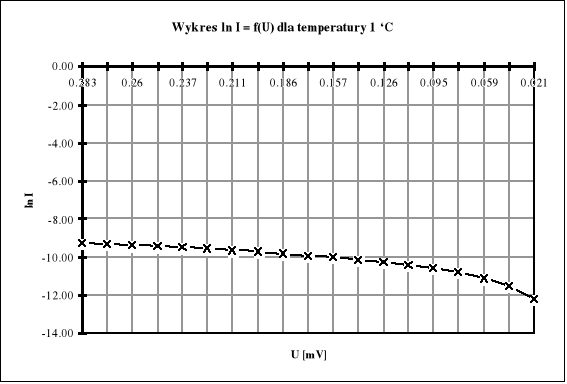
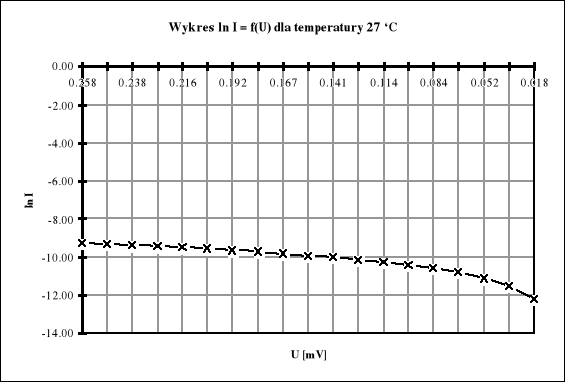
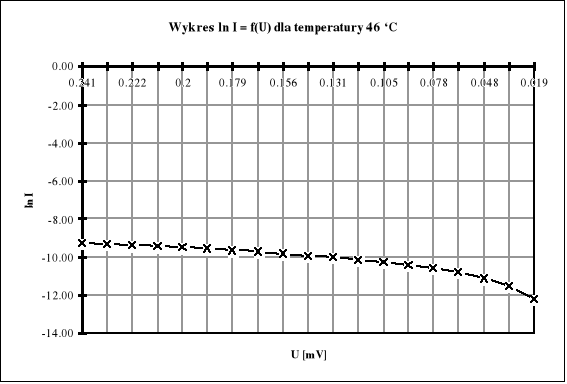
Z regresji liniowej obliczam wartości ln I_s dla poszczególnych temperatur.

Temperatura : 1^oC 27^oC 46^oC

ln I_s = -9.286 ln I_s = -9.31 ln I_s = -9.239

1/T = 0.0036 1/T = 0.0033 1/T = 0.0031

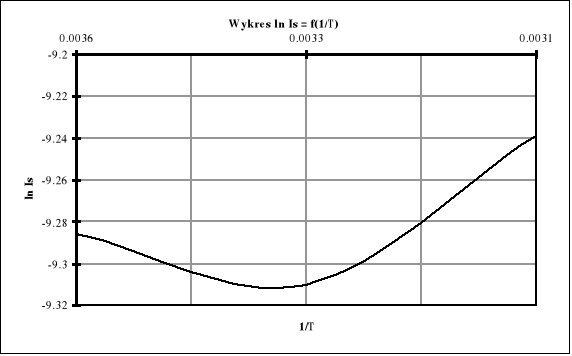
Stosując regresję liniową znajduję współczynnik nachylenia prostej regresji wykresu ln I_s = f(1/T).

a = -80.26

Δa = 0.036

Ze wzoru:

Obliczam wysokość bariery potenciału:

ϕ = - 6.917*10^-3

Metodą różniczki zupełnej obliczam Δϕ:

Ostatecznie Bariera potenciału na złączu P - N wynosi:

ϕ = (- 6.917 ± 0.003 )[mV/stop.]

Wnioski

Z uzyskanych w doświadczeniu wyników można wywnioskować , że badana była dioda germanowa . Ma ona barierę potencjału najbliższą wynikowi .

Wynik końcowy obarczony jest stosunkowo niewielkim błędem . Należy jednak zwrócić uwagę na to , że odchylenie standardowe po zastosowaniu regresji liniowej . Dużym błędem obarczone są natomiast bezpośrednie wyniki pomiaru .

p

I_dn

N_p

n

I_sn

N_n

a) b)

eϕ

- - - - - - - - - - - - -

- - - - - - - - - - - -

pasmo przewodnictwa

E_W

E_F

E_d

E_F

+ + + + + + + + + +

+ + + + + + + + + +

E_F

E_a

P_p

+ + + + + + +

P_n

I_sp

I_dp

pasmo walencyjne

Rys.200.2. Schemat energetyczny diody p-n

Rys.200.1 Pasma i poziomy energetyczne w półprzewodniku typu n (a) i w półprzewodniku typu p (b). E_F - Energia Fermiego, E_d - Energia domieszek donorowych, E_a - Energia domieszek akceptorowych.

---