2008-UŁ-Logistyka Zaopatrzenia-5

Metody ilościowe w logistyce zaopatrzenia - CD

4. Program produkcji - obliczanie popytu zależnego

Wielkość popytu zależnego zależy od:

• struktury konstrukcyjnej wyrobu,

• harmonogramów produkcji, oraz

• posiadanych zapasów (produkcji w toku, dostaw w drodze, itp.).

Struktura konstrukcyjna wyrobu - czyli analiza procesu wytwarzania produktu końcowego, jest uporządkowanym ciągiem operacji technologicznych. Analizę taką można wykonywać przy zastosowaniu pewnych metod graficznych, takich jak przykładowo: graf „drzewo produktu” bądź graf „Gozinto”.

Graf „drzewo produktu”

Jest to pewien kształt graficzny (zwany potocznie grafem), w którym wyodrębnia się następujące elementy:

• „Węzły” - czyli stanowiska pracy (bądź całe etapy produkcji) na których powstaje półprodukt lub produkt końcowy;

• „Strzałki” - przedstawiające kierunek przepływów materiałów pomiędzy wyróżnionymi węzłami (stanowiskami roboczymi);

• „Liczby” - czyli przypisane bezpośrednio do strzałek konkretne wielkości przepływu.

Przykład:

W pewnym przedsiębiorstwie produkuje się dwa różne rodzaje wyrobów gotowych: „produkt P1” oraz „produkt P2”. Do każdego z nich stosuje się nieco inny proces produkcji. Każdy z tych procesów przedstawiony za pomocą „drzewa produktu” wygląda następująco:

Rysunek: Drzewo produktu dla produktów: P1 oraz P2

P1 P2

Poziom 0

2 1 10 3 10

PP1 PP2 S1 PP3 S1

Poziom 1

7,5 10 5 5 10 10 15

S1 S2 S3 S1 S4 S1 S2

Poziom 2

Graf „drzewo produktu” jest znormalizowany i spełnia następujące warunki:

• Produkt końcowy jest ostatnim węzłem na poziomie 0 (czyli P1 i P2);

• Na poziomie 1 znajdują się węzły odpowiadające półproduktom i surowcom bezpośrednio wykorzystywanym w ostatniej fazie (operacji technologicznej) procesu produkcji;

• Na poziomie 2 zaznaczono węzły odpowiadające półproduktom i surowcom bezpośrednio wykorzystywanym w tworzeniu półproduktu z poziomu 1;

• Każdy węzeł z danego poziomu symbolizujący wykorzystany półprodukt bądź surowiec, może być początkiem tylko jednej strzałki kończącej się w węźle wyższego poziomu. Tak więc przykładowo, jeżeli surowiec S1 jest bezpośrednio wykorzystywany do produkcji PP1, PP2 oraz P1 to reprezentują go 3 różne węzły. Wielokrotne powtarzanie węzłów tego samego surowca czy półproduktu informuje, na jakich stanowiskach te surowce są potrzebne;

• Liczba przypisana strzałce informuje ile jednostek poprzednika jest potrzebne do wytworzenia jednej jednostki następnika.

Graf Gozinto

Jeżeli chcemy graficznie zilustrować jednoczesne wytwarzanie wielu produktów, do których produkcji potrzebne są te same półprodukty i surowce, a także są zaangażowane te same stanowiska pracy, to wówczas schemat jaki powstanie nosi nazwę „grafu Gozinto”.

W „grafie Gozinto” w odróżnieniu od „drzewa produktu”, każdy produkt jest reprezentowany przez jeden węzeł (nie ma powtórzeń węzłów), odpowiadający surowcom bądź półproduktom. Pozostałe elementy oznaczają to samo, co w „drzewie produktu”:

Rysunek: Graf Gozinto dla produktów P1 oraz P2

S1 P1

PP1

S2

PP2 P2

S3

PP3

S4

Ze względu na zbyt wiele elementów, które powinny być na tym schemacie, w grafie Gozinto pomija się liczby przypisane strzałkom. Dlatego też graf Gozinto jest uzupełniany specjalnym zestawieniem tabelarycznym, w którym zapisuje się niezbędne informacje, zarówno liczbowe jak i tekstowe.

Oto przykład takiej tabeli.

Tabela: Opis operacji do Grafu Gozinto

Węzeł początkowy (poprzednik)	Węzeł końcowy (następnik)	Wielkość przepływu	Jednostka przepływu	Opis słowny
S1 S1 S1 S1 S1 S2 S2 S3 S4 PP1 PP2 PP3	PP1 PP2 PP3 P1 P2 PP1 PP3 PP1 PP2 P1 P1 P2	7,5 5 10 10 10 10 15 5 10 2 1 3	kg / warstwę kg / warstwę kg / warstwę kg / szt. kg . szt. mb / warstwę mb / warstwę mb / wartwę mb / warstwę warstwa / szt. warstwa / szt. warstwa / szt.	7,5 kg żywicy do nasycenia 1 warstwy 5 kg żywicy do nasycenia 1 warstwy laminatu 10 kg żywicy do nasycenia 1 warstwy laminatu 10 kg żywicy do sklejania i prasowania warstw laminatu na 1 szt. Rury 10 kg żywicy do sklejania i prasowania warstw laminatu na 1 szt. rury 10 mb maty szklanej 0,2 mm do nasycenia żywicą na 1 warstwę laminatu 15 mb maty szklanej 0,2 mm do nasycenia żywicą na 1 warstwę laminatu 5 mb maty szklanej 0,5 mm do nasycenia żywicą na 1 warstwę laminatu 10 mb maty z włókna węglowego do nasycenia żywicą na 1 warstwę laminatu 2 warstwy laminatu na 1 szt. rury 1 warstwa laminatu na 1 szt. rury 3 warstwy laminatu na 1 szt. rury

5. Plan potrzeb materiałowych

Macierz jednostkowych nakładów wewnętrznych

(jedna z metod harmonogramowania produkcji)

W tej metodzie konstruuje się specjalną macierz, w której zawarte są wszystkie elementy z drzewa produktu jak również z grafu Gozinto. Zasady sporządzania tej macierzy:

• W kolumnach i wierszach obowiązuje ta sama kolejność wyznaczania węzłów,

• Węzły wpisuje się w następującej kolejności: najpierw wszystkie surowce, potem półprodukty, a na końcu wyroby gotowe.

Przykład sporządzenia macierzy jednostkowych nakładów wewnętrznych dla analizowanych wcześniej wyrobów gotowych P1 oraz P2:

Tabela: Macierz wyjściowa

Symbol	S1	S2	S3	S4	PP1	PP2	PP3	P1	P2
S1 S2 S3 S4 PP1 PP2 PP3 P1 P2	0 0 0 0 0 0 0 0 0	0 0 0 0 0 0 0 0 0	0 0 0 0 0 0 0 0 0	0 0 0 0 0 0 0 0 0	7,5 10 5 0 0 0 0 0 0	5 0 0 10 0 0 0 0 0	10 15 0 0 0 0 0 0 0	10 0 0 0 2 1 0 0 0	10 0 0 0 0 0 3 0 0

Dysponując taką macierzą wyjściową można obliczyć ilość potrzebnych surowców i półproduktów niezbędnych do wytworzenia z góry ustalonej wielkości produkcji końcowej.

W każdym węźle (zaznaczmy go symbolem „k”) powstają jakieś wyroby (wyroby gotowe lub półprodukty), na które istnieje określony popyt - zapotrzebowanie pierwotne (oznaczmy to symbolem „d_k”) oraz zapotrzebowanie wtórne (symbol „y_k”). Łączne zapotrzebowanie (symbol „r_k”) jest więc sumą popytów „d_k” oraz „y_k”. Można to zapisać wzorem: r_k = d_k + y_k.

Graficznie równanie to można zilustrować następująco:

Klient

d_k

K

y_k Kolejny węzeł

W zapisie macierzowym - symbolizującym wszystkie węzły jednocześnie - powyższe równanie ma postać: R = Y + D, gdzie:

R - wektor przedstawiający wytwarzaną na poszczególnych stanowiskach

produkcję, zarówno końcową jak również nie zakończoną.

Y - wielkości poszczególnych faz produkcji

kierowane do dalszego przetworzenia.

D - ilość i rodzaj wyrobów sprzedawanych na zewnątrz zakładu do klientów.

Jeżeli znane jest zapotrzebowanie na wyroby gotowe dla klientów (plan sprzedaży) - czyli wektor „D”, to należy obliczyć pozostałe parametry „R” i „Y”. W tym celu korzysta się z własności rachunku macierzowego, gdzie można przekształcić powyższy wzór: R = Y +D do postaci: Y = A ^x R

A więc: R = A ^x R + D

Teraz znane są już: macierz „A” oraz wektor „D”, a nie znany wektor „R”. Dalej więc korzystamy z własności macierzy i przekształcamy wzór do postaci:

,

Następnie wprowadzamy oznaczenie pomocnicze:

(Etapy tego przekształcenia pokazano w ramce)

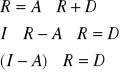
teraz mnożenie stronami przez:

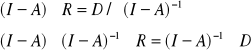
ponieważ:

dlatego:

w efekcie otrzymujemy:

następnie wprowadzamy oznaczenie pomocnicze:

Teraz równanie ma postać: R = V ^x D.

Składowe macierzy „V” wynikają ze struktury procesu produkcji. Natomiast składowe wektora „D” - określa się na podstawie informacji o przewidywanej sprzedaży. Mogą to być wielkości zamówień lub prognozy sprzedaży.

Równanie R = V ^x D pozwala na wyznaczenie zapotrzebowania na surowce i półprodukty, w sytuacji gdy znane jest zapotrzebowanie zewnętrzne odnoszące się do jednego okresu (na dany moment czasu). Ale można to bez trudu rozszerzyć na przypadki, gdy znamy zapotrzebowanie zewnętrzne na pewien skończony ciąg okresów. Przykładowo na konkretne dni, tygodnie lub miesiące w określonym przedziale czasu. W takiej sytuacji parametr „D” jest macierzą wektorową, której kolumny przedstawiają zapotrzebowanie na kolejne okresy D = [d1, d2, ...., dn].

Przykład wyznaczenia popytu netto na surowce i półprodukty potrzebne do wytworzenia analizowanych wyrobów gotowych: P1 oraz P2:

Kolejność postępowania:

1. Na podstawie macierzy „A” wyznaczamy macierz „I - A”:

Tabela: Przekształcenie macierzy wyjściowej

Symbol	S1	S2	S3	S4	PP1	PP2	PP3	P1	P2
S1 S2 S3 S4 PP1 PP2 PP3 P1 P2	1 0 0 0 0 0 0 0 0	0 1 0 0 0 0 0 0 0	0 0 1 0 0 0 0 0 0	0 0 0 1 0 0 0 0 0	-7,5 -10 -5 0 1 0 0 0 0	-5 0 0 -10 0 1 0 0 0	-10 -15 0 0 0 0 1 0 0	-10 0 0 0 -2 -1 0 1 0	-10 0 0 0 0 0 -3 0 1

2. Następnie wyznaczamy macierz „V” (czyli odwracamy macierz „I-A”):

Symbol	S1	S2	S3	S4	PP1	PP2	PP3	P1	P2
S1 S2 S3 S4 PP1 PP2 PP3 P1 P2	1 0 0 0 0 0 0 0 0	0 1 0 0 0 0 0 0 0	0 0 1 0 0 0 0 0 0	0 0 0 1 0 0 0 0 0	7,5 10 5 0 1 0 0 0 0	5 0 0 10 0 1 0 0 0	10 15 0 0 0 0 1 0 0	30 20 10 10 2 1 0 1 0	40 45 0 0 0 0 3 0 1

3. Na podstawie planu sprzedaży ustalamy zapotrzebowania na surowce - macierz symbolizującą parametr „D”:

Uwaga: Jeżeli to zapotrzebowanie ma być na 1 konkretny okres to wówczas macierz „D” będzie miała tylko jedną kolumnę. Natomiast gdy zapotrzebowanie na dany okres jest rozbite na okresy jednostkowe, to wówczas macierz „D” będzie miała tyle kolumn ile jest okresów jednostkowych. W analizowanym przykładzie jest sytuacja, gdzie zamówienie od klientów rozbite jest na 10 okresów jednostkowych. Wielkości tych zamówień są następujące:

Tabela: Macierz przedstawiająca zapotrzebowanie na wyroby gotowe: P1 oraz P2

Symbol	Tydzień
	1	2	3	4	5	6	7	8	9	10
S1 S2 S3 S4 PP1 PP2 PP3 P1 P2	0 0 0 0 0 0 0 60 150	0 0 0 0 0 0 0 72 130	0 0 0 0 0 0 0 75 125	0 0 0 0 0 0 0 80 115	0 0 0 0 0 0 0 85 115	0 0 0 0 0 0 0 90 110	0 0 0 0 0 0 0 100 100	0 0 0 0 0 0 0 105 100	0 0 0 0 0 0 0 110 90	0 0 0 0 0 0 0 120 90

4. Po wykonaniu działania: R = V ^x D mamy wyznaczone „R”, czyli zapotrzebowanie na surowce i półprodukty:

Tabela: Plan potrzeb materiałowych na surowce i półprodukty potrzebne do produkcji wyrobów: P1 oraz P2

Symbol	Nazwa	Jednostka	Tydzień
	materiału	Miary	1	2	3	4	5	6	7	8	9	10
S1 S2 S3 S4 PP1 PP2 PP3 P1 P2	żywica mata mata mata laminat laminat laminat rura rura	kg mb mb mb warstwa warstwa warstwa szt. szt.	7800 7950 600 600 120 60 450 60 150	7360 7290 720 720 144 72 390 72 130	7250 7125 750 750 150 75 375 75 125	7000 6775 800 800 160 80 345 80 115	7150 6875 850 850 170 85 345 85 115	7100 6750 900 900 180 90 330 90 110	7000 6500 1000 1000 200 100 300 100 100	7150 6600 1050 1050 210 105 300 105 100	6900 6250 1100 1100 220 110 270 110 90	6800 6000 1200 1200 240 120 240 120 90

Z tej tabeli wynika już konkretna ilość surowców i półproduktów, które są potrzebne w konkretnych momentach czasu, na realizację produkcji obu wyrobów gotowych.

W skróconej wersji zapotrzebowanie na same surowce wygląda następująco:

Tabela: Plan potrzeb materiałowych na surowce do produkcji wyrobów: P1 oraz P2

Symbol	Jednostka	Tydzień
	Miary	1	2	3	4	5	6	7	8	9	10	Razem
S1 S2 S3 S4	kg mb mb mb	7800 7950 600 600	7360 7290 720 720	7250 7125 750 750	7000 6775 800 800	7150 6875 850 850	7100 6750 900 900	7000 6500 1000 1000	7150 6600 1050 1050	6900 6250 1100 1100	6800 6000 1200 1200	71510 68115 8970 8970

5. Wybór dostawcy

Wybór dostawcy powinien być poprzedzony opracowaniem listy potencjalnych dostawców. Wykorzystuje się w tym celu katalogi, cenniki, materiały reklamowe bądź spisy wytwórców z wystaw specjalistycznych.

Właściwego wyboru źródła zakupu dokonuje się w wyniku zastosowania zestawienia szeregu kryteriów oceny. Głównym celem tych kryteriów jest dążenie do minimalizacji łącznych kosztów związanych z zakupami materiałów i utrzymaniem zapasów oraz stworzenie podstaw do niezakłóconego przebiegu produkcji, przy zapewnieniu odpowiedniego poziomu jakości dostarczanych dóbr.

Przykładowy zestaw kryteriów oceny przedstawia się następująco:

• cena zakupu i ewentualne upusty,

• jakość towaru,

• warunki dostawy (ilości oferowane w jednorazowej dostawie),

• gwarancje i uwzględnianie roszczeń,

• sytuacja finansowa dostawcy,

• opinia o dostawcy wśród innych odbiorców,

• zdolność do adaptacji zmian w popycie,

• system łączności,

• lokalizacja (odległość dostawcy od zakładu produkcyjnego),

• możliwość składowania u dostawcy.

Do oceny stosuje się wiele różnorodnych narzędzi, takich jak przykładowo:

• Model silnych i słabych stron dostawcy,

• Metodę punktową,

• Metodę graficzną - („wykres radarowy”, itp.).

Model silnych i słabych stron dostawcy

Nazwa	Ocena
Dostawcy:	Niewystarczająca	Słaba	Wystarczająca	Dobra	Znakomita
Cechy	(0)	(1)	(2)	(3)	(4)
Możliwości produkcyjne i techniczne					X
Pozycja finansowa			X
Jakość produktu					X
Rzetelność dostawy			X
Serwis					X
Ogólny wynik: 4 + 2 + 4 + 2 + 4 = 16
Przeciętny wynik: 16 : 5 = 3,2

Metoda punktowa

Kryteria	Waga	Dostawca 1	Dostawca 2	Dostawca 3
Dostawa na czas	4	4 16	2 8	1 4
Czas realizacji zamówienia	5	5 25	4 20	3 15
Cena zakupu	4	4 16	5 20	1 4
Serwis	4	3 12	2 8	5 20
Gwarancja zakupu	3	1 3	3 9	2 6
Zyskowność	5	4 20	3 15	5 25
Kwalifikacje pracowników dostawcy	4	5 20	4 16	3 12
Gotowość do realizacji specyfikacji zamówieniowej	3	5 15	1 3	4 12
SUMA	X	127	99	98

Inną wersją tej metody jest następujący przykład. W tym wariancie metoda ta wymaga zastosowania dwóch tabel. W tabeli nr 1 wpisuje się rzeczywiste dane o dostawcach. Natomiast tabela nr 2 służy do obliczeń:

TABELA 1

Kryteria	Dostawca 1	Dostawca 2	Dostawca 3
Cena	100 PNZ	106 PNZ	104 PNZ
Terminy dostaw	3 tygodnie	Do dyspozycji	10 tygodni
Jakość	Konieczność kilku udoskonaleń, aby dotrzymać oczekiwanych warunków	Zdolność do spełnienia oczekiwanych warunków	Potrzeba dużych wysiłków, aby spełnić oczekiwane warunki
Opakowanie / Transport	„franco” wolne od kosztów	5 % ceny	3,5 % ceny
Gwarancja	1 rok	6 miesięcy	8 miesięcy
Warunki płatności	90 dni	30 dni	90 dni
Kary za zwłokę	-	-	-
Rezerwa zapasów	80 % partii	Całość partii	40 % partii

TABELA 2

Kryteria	Współczynnik ważony	Dostawca 1	Dostawca 2	Dostawca 3
Cena	20	20	14	16
Terminy dostaw	15	12	15	5
Jakość	30	24	30	18
Opakowanie / transport	8	8	0	0
Gwarancja	10	10	4	6
Warunki płatności	5	5	0	5
Kary za zwłokę	5	0	0	0
Rezerwa zapasów	7	6	7	4
Ocena ogólna	100	85	70	54

Metoda graficzna „wykres radarowy”

Kryterium	Cechy
1. Jakość materiału	poziom jakości trwałość czystość
2. Cena	poziom w stosunku do konkurencji warunki płatności elastyczność zmian
3. Terminowość dostaw	3.1. długość terminów 3.2. solidność w dotrzymaniu terminów 3.3. zachowanie wielkości dostaw
4. Dodatkowe usługi	własny transport utrzymywanie zapasów

Każda cecha punktowana jest w dowolnej skali. Załóżmy że 5-cio punktowa skala oznacza: 1-ocena zła, 2 -dostateczna, 3 -wystarczająca (neutralna), 4 -dobra, 5 - ocena bardzo dobra.

W zależności od liczby dostawców, dla każdego z osobna sporządza się wykres radarowy w postaci:

Dostawca 1

Cena

Jakość

materiału

Terminowość dostaw

Usługi dodatkowe

Dostawca 2

Cena

Jakość

materiału

Usługi dodatkowe Terminowość dostaw

12

Ocena „5”

Ocena „4”

Ocena „2”

Ocena „3”

---