5. Rozwinięcie sygnałów okresowych w szereg względem funkcji trygonometrycznych w przedziale nieskończonym (-∞,∞).

Dwa sygnały nazwiemy ortogonalnymi, jeżeli ich iloczyn skalarny, a tym samym energia wzajemna są równe zero:

- są one krańcowo „nie podobne” do siebie

W przestrzeni jest określona baza ortonormalna, jeżeli przestrzeń ta jest przestrzenią Hilberta sygnałów o skończonej wartości energii i określonych na ograniczonym lub nieograniczonym przedziale czasu (t₁, t₂), a w tym przedziale dany jest zbiór funkcji {u₁, u_2,…,u_k,…} parami ortogonalnych i mających jednostkową normę.

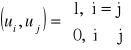
Dowolny sygnał x(t) rozwiniemy w uogólniony szereg Fouriera względem danej bazy

współczynniki f. bazowe

Współczynniki tego szeregu można obliczyć mnożąc przez dowolny k-ty element bazy i obliczając całkę w przedziale czasu, w którym określone są sygnały

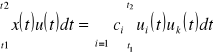
uwzględniając ortonormalność bazy

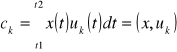
Można wykazać, zbiór funkcji trygonometrycznych

{cosiω₀t, siniω₀t}, i=0,1,2…

tworzy w przedziale (t₀, t₀+T), gdzie T=2π/ ω₀ układ ortogonalny zupełny.

Dowolny sygnał x(t) można zatem rozwinąć w przedziale (t₀, t₀+T) w szereg postaci:

Współczynniki tego rozwinięcia wyznaczamy ze wzorów:

gdzie:

Dla funkcji trygonometrycznych

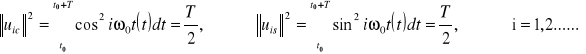
zatem:

Zatem dowolny sygnał x(t) można rozwinąć w szereg trygonometryczny w przedziale (t₀,t₀+T)

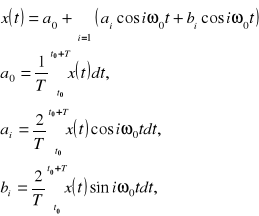
Natomiast ostatecznie dowolny sygnał okresowy można rozwinąć w szereg trygonometryczny w przedziale nieskończonym

-współczynniki j.w.

W ogólnym przypadku sygnał okresowy zawiera składową stałą - niezależną od czasu i nieskończony zbiór składowych harmonicznych o pulsacjach ωn=nω

Każda składowa scharakteryzowana jest amplitudą c_n i fazą φ_n. Otrzymujemy stąd równoważną postać trygonometrycznego szeregu Fouriera

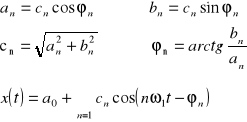
9. Przekształcenie Z i jego podstawowe własności.

Przekształcenie Z odgrywa dla sygnałów dyskretnych podobną rolę jak przekształcenia Laplace'a i Fouriera dla sygnałów analogowych

Niech {x_k}={x₀, x₁, …} będzie ciągiem liczbowym, skończonym lub nieskończonym, którego elementy są próbkami pewnego sygnału analogowego. Temu ciągowi przyporządkujemy w jednoznaczny sposób funkcję zmiennej zespolonej z, do której jest zbieżny szereg zmiennej o ujemnych potęgach

Funkcja ta, jeżeli istnieje jest transformatą Z ciągu{x_k). Dzięki właściwości ciągów liczbowych można badać metodami analizy matematycznej badając ich transformatę Z.

Powyższa transformata jest transformatą jednostronną. Jest ona równa transformacie dwustronnej
dla sygnałów przyczynowych, a właśnie takimi się zajmujemy.

Przekształcenie Z nie jest zbieżne dla wszystkich wartości zmiennej , dlatego musimy określić obszar zbieżności - zbiór wartości, dla których transformata ciągu jest zbieżna. Szereg jest zbieżny w pierścieniu płaszczyzny z

R_x-<|z|<R_x+

może osiągać zero może dążyć do nieskończoności

Zerami funkcji X(z) - pierwiastkami wielomianu licznika, są te wartości z: X(z)=0

Biegunami funkcji są te wartości z, dla których X(z)→ ∞ (mogą występować dla z=0 lub z=∞)

Bieguny nie mogą występować w obszarze zbieżności ponieważ transformata Z nie jest zbieżna w biegunie.

Odwrotne przekształcenie Z:

- operacja całkowania odbywa się po konturze zamkniętym, obejmującym początek płaszczyzny zespolonej, leżącym wewnątrz obszaru zbieżności.

Własności przekształcenia Z

obszar zbieżności wymiernej transformaty Z nie może zawierać żadnych biegunów, jest on zatem ograniczony przez bieguny, przez zero, lub nieskończoność (transformata Z nie jest zbieżna w biegunie)

twierdzenia graniczne

suma wszystkich próbek sygnału równa jest transformacie Z tego sygnału dla z =1

jeśli x(n) jest przyczynowe to

Jeżeli dane są pary transformat

x(n)↔X(z) oraz y(n↔y(z)

twierdzenie o liniowości

ax(n)+ by(n) ↔ aX(z)+ bY(z)

twierdzenie o przesunięciu w dziedzinie czasu

x(n-n₀) ↔ z ^-no X(z)

twierdzenie o mnożeniu przez ciąg wykładniczy (zespolony)

x(n)a^-n↔ X(az)

twierdzenie o splocie w dziedzinie czasu

x(n)*y(n}↔X(z)Y(z)

twierdzenie o splocie w dziedzinie częstotliwości

twierdzenie o różniczkowaniu w dziedzinie czasu

---