Kamil Dobrzyń gr. 3

Ćwiczenie 27: Wyznaczanie stosunku
dla powietrza.

Gaz doskonały to fikcyjny, idealny gaz, którego cząsteczki są nieskończenie małe i nie zachodzi między nimi wzajemne przyciągania, ani nie występują w nich drgania wewnętrzne.

Dla powyższego gazu energia wewnętrzna U jest równa sumie energii kinetycznej ruchu postępowego i obrotowego cząsteczek. Aby obliczyć tą energię trzeba skorzystać z pojęcia stopni swobody, czyli liczby niezależnych współrzędnych określających położenie cząsteczki w przestrzeni. I tak dla cząsteczek jednoatomowych stopień swobody i=3 odpowiadające trzem współrzędnym przestrzennym bądź też trzem składowym prędkości. Cząsteczka dwuatomowa posiada pięć stopni swobody (i=5), ponieważ do trzech stopni swobody ruchu postępowego dochodzą dwa stopnie swobody związane z obrotem cząsteczki jako ryły sztywnej wokół dwóch prostopadłych względem siebie osi. Cząsteczki trój- lub więcej atomowa posiada sześć stopni swobody (i=6) ponieważ dla takich cząsteczek możliwe są 3 osie obrotu.

Wzór ogólny na obliczenie energii kinetycznej cząsteczek:

(1)
; gdzie:

i- stopień swobody

k- stała Boltzmanna

T- temperatura w Kelwinach

Dla jednego mola gazu jego energia wewnętrzna U jest równa:

(2) U=NE; gdzie:

N- liczba Avogardo

E- energia jednej cząstki

Więc wyprowadzając:

(3)
, gdyż:

R- stała gazowa

Ilość energii potrzebna do odniesieni temperatury jednego mola cząsteczek o jeden Kelwin nosi nazwę ciepła molowego danej substancji.

Ciepło molowe danej substancji zależy od warunków, w jakich gaz jest ogrzewany, i tak w przypadku ogrzewania izochorycznego, gdzie nie zmienia się objętość (V) dostarczone ciepło służy do zwiększenia energii wew. gazu. Ponieważ V= const. Praca sił wewnętrznych gazu równa jest zeru. W tym przypadku mamy do czynienia z ciepłem molowym przy stałej objętości Cv.

Gdy ogrzewamy gaz pod stałym ciśnieniem- przemiana izobaryczna- ciepło zostaje zużyte dodatkowo na wykonanie pracy przeciw siłom zewnętrznym- gaz rozszerza się (gdyż p=const.). Mamy wtedy doczynienia z ciepłem molowym przy stałym ciśnieniu Cp.

Cv można określić jako stosunek przyrostu energii wewnętrznej jednego mola gazu do zmiany temperatury wywołanej tym przyrostem.

(4)
; gdy
otrzymujemy:

(5)

Cp jest większe od Cv o pracę W, wykonana przez mol gazu przy rozszerzaniu się podczas wzrostu temperatury o 1 stopień.

(6) Cp=Cv+W

Praca wykonana przy zwiększaniu objętości:

(7) W= p
=p(V2-V1);

Za równaniem Clapeyrona:

(8) pV1=RT; pV2=R(T+1), więc W=R(T+1)-RT=R

Wynika z tego, że stała gazowa R jest liczbowo równa pracy wykonanej przez jeden mol gazu pod stałym ciśnieniem przy podwyższaniu temperatury układu o jeden Kelwin, więc:

(9) Cp= Cv+ R; podstawiając za Cv:

(10)

jest stosunkiem ciepła molowego Cp do ciepła molowego Cv:

(11)

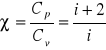
Przemiany:

Wtłoczony pod ciśnieniem gaz do balonu znajduje się pod ciśnieniem. Gaz określony jest parametrami:

1.Ciśnienie (p+ p₁)- suma ciśnienia atmosferycznego i nadwyżki ciśnienia spowodowanej wtłoczeniem powietrza do balonu;

2.objętość gazu przed rozprężeniem;

3. temperaturę otoczenia.

Ciśnienie jest wprost proporcjonalne do różnicy poziomów cieczy w manometrze, ponieważ p= ρgh

Po otwarciu korka butli, w wyniku czego gaz rozpręża się adiabatycznie (oziębia się), w tym stanie parametry gazu zmieniają się:

1. ciśnienie (p) równe jest ciśnieniu adiabatycznemu

2. Objętość po rozprężeniu jest większa

3. Temperatura jest niższa

Po zamknięciu korka gaz ogrzewa się i po kilku minutach osiąga ponownie temperaturę otoczenia. W czasie zachodzącej przemiany izochorycznej powstaje nadwyżka ciśnienia, co obserwujemy na manometrze (ustala się różnica poziomów cieczy)

Stan trzeci układu określany jest przez następujące parametry:

Ciśnienie- p+p₂

Objętość V₂

Temperaturę otoczenia

Przejście ze stanu pierwszego w stan drugi określa równanie Poissona:

(p₀+p₁)V
=p₀V

Przejście ze stanu 1 przez stan 2 w stan 3 można zastąpić przemianą izotermiczną, w której gaz przechodzi ze stanu 1 bezpośrednio w stan 3 w stałej temperaturze otoczenia.

Dla tego przejścia zastosujemy wzór Boyle'a i Mariotte'a:

(p₀+p₁)V₁=(p₀+p₂)V₂

Z powyższych równań obliczamy:

Pomiar:

1. Sprężyć powietrze w naczyniu i poczekać na wyrównanie temperatury między gazem i otoczeniem (ustaje wahanie cieczy w manometrze). Odczytujemy różnicę poziomów h₁.

2. Wyjąć korek i po wyrównaniu ciśnienia z otoczeniem natychmiast go włożyć. Na skutek ogrzania powietrza w naczyniu powstaje nadciśnienie h₂ wskazywane przez manometr.

Pomiar:	T	h1	h2	h1+h2
		k	mm	mm	mm	-	-
1
2
3
4
5
6
7
8
9
10

Obliczenia:

---