Politechnika Lubelska |
Laboratorium Elektrotechniki |
|||
w Lublinie |
Ćwiczenie nr 7 |
|||
Józwik Tomasz, Kadłubowski Krzysztof Szczęśniak Mirosław, Łakomy Mirosław |
Semestr III |
Grupa: 3.5A |
Rok akademicki: 1996/97 |
|
Temat ćwiczenia: Analiza przebiegów odkształconych. |
Data wykonania: 25,11,96 |
Ocena: |
||
Celem ćwiczenia jest poznanie metody pomiaru zawartości wyższych harmonicznych
w prądach odkształconych analizatorem harmonicznych.
Przeprowadzenie ćwiczenia polega na wykonaniu pomiarów oraz niezbędnych obliczeń.
Otrzymane dane notuję w tabelach.
3.Pomiar udziału harmonicznych w prądzie magnesującym transformatora.
POMIARY |
OBLICZENIA |
|||||||||||||
|
U |
I |
I2/I1 |
I3/I1 |
I4/I1 |
I5/I1 |
I6/I1 |
I7/I1 |
I9/I1 |
I1 |
I3 |
I5 |
I7 |
I9 |
L.p. |
V |
mA |
% |
% |
% |
% |
% |
% |
% |
mA |
mA |
mA |
mA |
mA |
1 |
177 |
50 |
6 |
29 |
0 |
2.5 |
0 |
2 |
8 |
47.8 |
13.9 |
1.19 |
0.96 |
3.82 |
2 |
200 |
60 |
6 |
30 |
0 |
3 |
0 |
2 |
8 |
57.1 |
17.1 |
1.71 |
1.14 |
4.57 |
3 |
210 |
70 |
6 |
32 |
0 |
3 |
0 |
2 |
8 |
66.3 |
21.2 |
1.99 |
1.33 |
5.31 |
4 |
220 |
75 |
6 |
33 |
0 |
4 |
0 |
2 |
8 |
70.9 |
23.4 |
2.13 |
1.42 |
5.67 |
5 |
230 |
85 |
6 |
34 |
0 |
4 |
0 |
2 |
8 |
80 |
27.2 |
3.2 |
1.6 |
6.4 |
6 |
250 |
110 |
6 |
37 |
0 |
4 |
0 |
2 |
8 |
102 |
37.9 |
4.1 |
2.05 |
8.21 |
Przykładowe obliczenia dla U=177 V :
dodatkowo uwzględniając:
otrzymuję:
stąd obliczam wszystkie prądy:
Na podstawie przeprowadzonych pomiarów wykreśliłem zależności i oraz widmo harmonicznych mierzonego przebiegu.
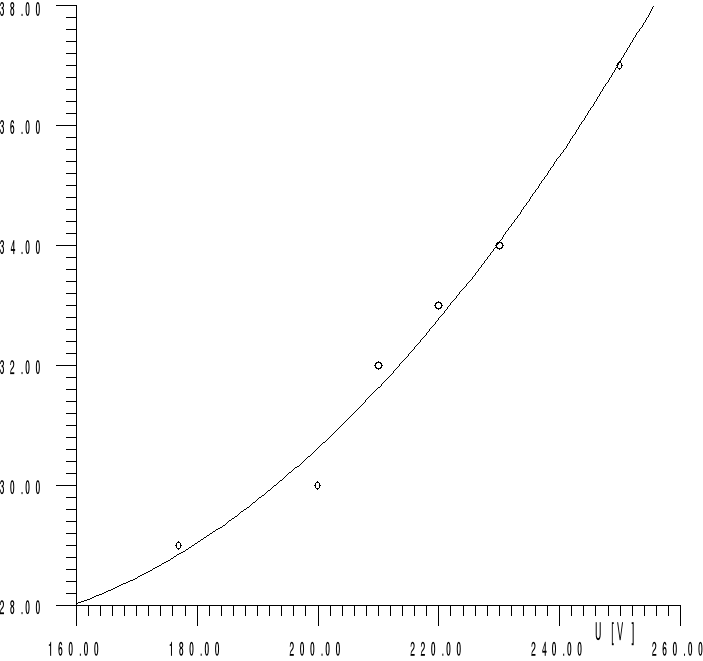
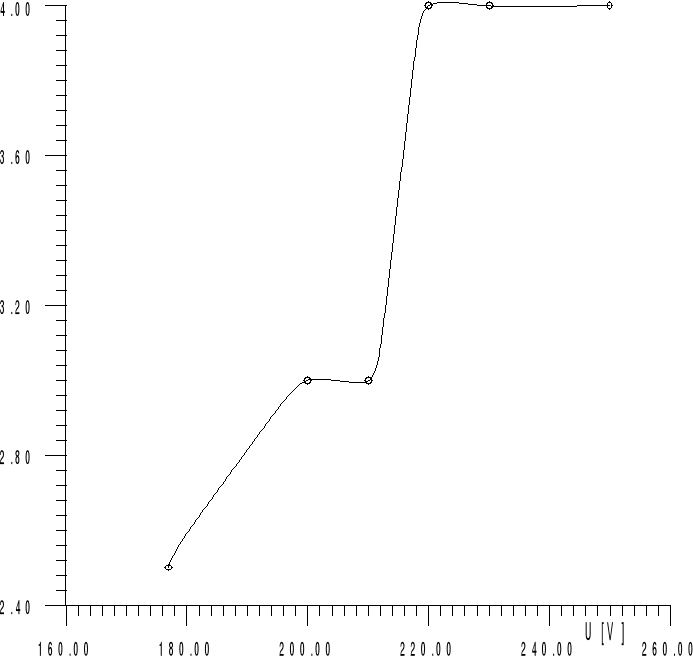
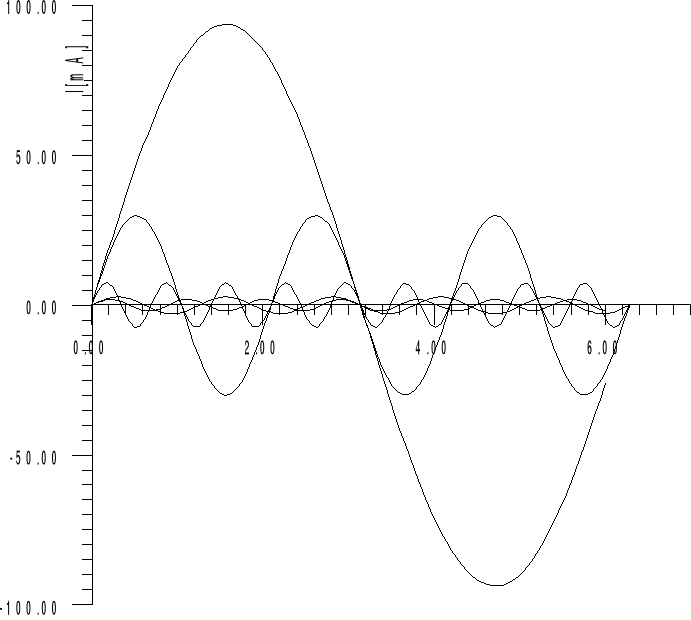
wt
3.Pomiar udziału harmonicznych w napięciu na wyjściu układu do prostowania jednopołówkowego.
POMIARY |
|
|
|
|
|
|
|
|
|
|||||||||
|
U1 |
U2 |
C |
U0/U1 |
U2/U1 |
U3/U1 |
U4/U1 |
U5/U1 |
U6/U1 |
|||||||||
L.p. |
V |
V |
μF |
% |
% |
% |
% |
% |
% |
|||||||||
1 |
20 |
8.5 |
- |
217.5 |
22 |
1 |
3 |
0 |
0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
20 |
9.8 |
60 |
270 |
19 |
3 |
2 |
1.5 |
0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
OBLICZENIA |
|||||||
|
U0 |
U1 |
U2 |
U3 |
U4 |
U5 |
U6 |
L.p. |
V |
V |
V |
V |
V |
V |
V |
1 |
7.69 |
3.535 |
0.778 |
0.035 |
0.106 |
- |
- |
|
|
|
|
|
|
|
|
2 |
9.17 |
3.396 |
0.645 |
0.102 |
0.068 |
0.051 |
- |
|
|
|
|
|
|
|
|
Przykładowe obliczenia dla prostowania bez wygładzania napięcia:
(*)
po uwzględnieniu tych zależności otrzymuję:
obliczam amplitudy wyższych harmonicznych i wartość składowej stałej korzystając z
zależności (*), wyniki zamieszczam w tabeli.
Pomiar udziału harmonicznych w przebiegu prostokątnym i trójkątnym.
|
POMIARY |
OBLICZENIA |
|
||||||||
L.p. |
U2/U1 |
U3/U1 |
U5/U1 |
U7/U1 |
U9/U1 |
U2/U1 |
U3/U1 |
U5/U1 |
U7/U1 |
U9/U1 |
sygnał |
|
% |
% |
% |
% |
% |
% |
% |
% |
% |
% |
|
1 |
12 |
34 |
16 |
10 |
6 |
- |
33.3 |
20 |
14.3 |
11.11 |
prost. |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
7 |
12 |
4 |
2 |
1 |
- |
11.11 |
3.99 |
2.035 |
1.237 |
trójk. |
|
|
|
|
|
|
|
|
|
|
|
|
Obliczenia dla sygnału prostokątnego:
Przebieg prostokątny w ujęciu analitycznym jest funkcją okresową, nieparzystą i ponadto antysymetryczną względem osi odciętych. Dlatego w rozwinięciu w szereg Fouriera nie występuje współczynnik an. To pociąga za sobą zerowanie się cosinusów, a także składowej stałej. Można więc wnioskować, że w ujęciu matematycznym sygnał odkształcony nie będzie zawierał składowej stałej, a także harmonicznych parzystych. Jak widać z tabeli nie jest to zgodne z wynikami otrzymanymi doświadczalnie. Z tego można wnioskować, że używany analizator niezbyt dokładnie wskazywał zawartość harmonicznych w sygnale, mogło to być związane z niedokładnym dostrojeniem filtru.
Dla sygnału prostokątnego szereg Fouriera przyjmie postać:
pamiętając, że n jest liczbą nieparzystą oraz Um=7.5 V otrzymuję szukane wartości.
Np.
n=1
n=3
stąd
Wnioski:
W przebiegach antysymetrycznych (spełniających symetrię względem osi odciętych) i gdy rzędne funkcji okresowej powtarzają się co pół okresu ze zmienionym znakiem występują tylko harmoniczne nieparzyste. W przebiegach symetrycznych względem osi rzędnych występują w rozwinięciu funkcji w szereg Fouriera czynniki tylko cosinusowe, ponieważ sinus jest funkcją nieparzystą. W funkcjach symetrycznych względu początku układu współrzędnych rozwijanych w szereg Fouriera występują tylko składniki sinusowe, ponieważ funkcja cosinus jest funkcją parzystą.
Wyliczony współczynnik ak decyduje o wartości amplitudy danej harmonicznej.
Analiza układów w ćwiczeniu przebiegała zgodnie z podstawami teoretycznymi. Nie zauważono znaczących rozbieżności pomiędzy wynikami pomiarów, a poznaną na wykładach teorią.
Analizę udziału harmonicznych w przebiegach przeprowadzono dla napięcia sinusoidalnego, przebiegu sinusoidalnego wyprostowanego, jak również dla trójkątnego i prostokątnego.
Każda z powyższych analiz dokonywana była na oddzielnym stanowisku pomiarowym, którego przygotowanie polegało jedynie na dostrojeniu filtra w analizatorze.
Wyszukiwarka