Politechnika Śląska w Gliwicach

Wydział Mechaniczny Technologiczny

Kierunek MiBM

LABORATORIUM Z MECHANIKI

Temat:

BADANIE RUCHU PŁASKIEGO CIAŁA SZTYWNEGO Z WYKORZYSTANIEM WAHADŁA MAXWELLA.

Sekcja: 2

Grupa : 5

1.Lipka Piotr 2.Trzaskowski Marek 3.Gorzeń Krzysztof 4.Szum Grzegorz 5.Respondek Leszek 6. Trzaskalik Łukasz 7. Mura Marcin

1. Cel ćwiczenia.

Celem ćwiczenia jest badanie prawa zachowania energii mechanicznej w zamkniętym układzie zachowawczym na przykładzie ciała sztywnego poruszającego się ruchem płaskim. Do tego celu wykorzystujemy wahadło Maxwella.

2. Wstęp teoretyczny.

Wahadło Maxwella to krążek K osadzony na cienkiej osi OO. Do obu końców tej osi przywiązane są dwie nici, na których zawieszone jest wahadło. Obracając krążek w palcach nawijamy nici na oba końce osi, po czym badany układ uwalniamy. Zaczyna on powoli spadać, a odwijając się z nici nabiera coraz większej prędkości liniowej i obrotowej. W najniższym położeniu krążek osiąga największą prędkość w ruchu obrotowym i ponownie zaczyna nawijać się na nici.

W zjawisku tym możemy zaobserwować zmianę energii potencjalnej Ep krążka, którą zyskał on dzięki podniesieniu na wysokość h na energię kinetyczną Ek. Z prawa zachowania energii mechanicznej w zamkniętym układzie zachowawczym wynika równość obu form energii, czyli:

Ep = Ek,

Ep - energia potencjalna układu w położeniu najwyższym,

Ek - energia kinetyczna układu w najniższym położeniu krążka.

Ponieważ krążek wykonuje jednocześnie ruch postępowy i ruch obrotowy, energia kinetyczna układu jest sumą energii kinetycznej ruchu postępowego Ekp i energii kinetycznej ruchu obrotowego Eko, skąd:

Ep = Ekp + Eko,

Ekp i Eko charakteryzują poniższe zależności:

Ekp = ½ mv²_k,

Eko = ½ Iω²_k

gdzie: m - masa całkowita układu

g - przyspieszenie ziemskie,

h - wysokość na którą zostanie podniesiona badana bryła,

vk - prędkość liniowa środka krążka osiągnięta w najniższym położeniu,

ωk - prędkość obrotowa osiągnięta w najniższym położeniu krążka.

Masę krążka K można zmieniać przez nałożenie jednego z trzech dołączonych do przyrządu pierścieni P, zmieniając w ten sposób warunki pomiaru.

Przekształcając powyższe zależności otrzymujemy:

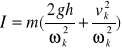
Uwzględniając zależność pomiędzy prędkością liniową i kątową wahadła :

gdzie D - dla warunków naszego ćwiczenia określić musimy jako średnicę zewnętrzną osi mierzoną wraz z nawiniętą na nią nicią.

Otrzymujemy więc zależność na wartość momentu bezwładności wahadła w postaci:

Krążek opadając porusza się ruchem jednostajnie przyspieszonym z prędkością początkową równą zero. Więc jego prędkość liniowa w najniższym położeniu wynosi:

gdzie t - czas ruchu krążka pomiędzy najwyższym i najniższym jego położeniem.

Podstawiając powyższą zależność otrzymujemy zależność na moment bezwładności::

Możemy również wyznaczyć momenty bezwładności dla konkretnych brył geometrycznych. I tak moment bezwładności osi Io w kształcie pełnego walca względem osi geometrycznej przybiera postać:

gdzie: m₀ - masa osi,

d₀ - średnica zewnętrzna osi.

:

gdzie m_p - masa pierścienia

D_p średnica zewnętrzna pierścienia.

Moment bezwładności bryły sztywnej wahadła Maxwella jest sumą wyżej wymienionych momentów bezwładności:

I = I₀ + I_k + I_p

3. Opracowanie wyników pomiarów.

Obliczamy wartości momentów bezwładności:

1. Wyznaczona wartość momentu bezwładności:

I = 7,58*10^-4 [kg*m²]

2. Względny błąd:

δ = 10,49 %

4. Wnioski.

Ćwiczenie pozwoliło na doświadczalne wyznaczenie wartości momentu bezwładności bryły przy pomocy wahadła Maxwella. Błąd wyznaczonej wartości w porównaniu z wartością teoretyczną wyniósł ok. 10,5 %.

Na dokładność pomiarów wpływają błędy pomiarów poszczególnych wielkości składowych, takich jak poszczególne masy, czy średnice.

Masa nici, która została pominięta, jest niewielka w porównaniu do pozostałych elementów układu, więc jej masa nie wpływa w sposób znaczący na wyniki pomiarów.