Wiktor Kołwzan
Logika pragmatyczna
(wykłady zebrane)
Wrocław 2007
Spis treści
Wprowadzenie
Każdemu, kto rozpoczyna studiowanie jakiejś dziedziny wiedzy, zwłaszcza matematyki, poważne trudności sprawia wdrożenie się do ścisłego formułowania myśli, zdobycie umiejętności poprawnego wnioskowania, uświadomienie na czym poprawne wnioskowanie powinno być oparte, przyswojenie, a zwłaszcza zrozumienie podstawowych pojęć. Trudności te płyną z wielu źródeł. Pierwszym z nich jest brak odpowiedniego przygotowania w zakresie logiki matematycznej w jej pragmatycznym wymiarze, czyli wymiarze nie tylko formalnym, lecz również treściowym - czyli rozumienia, czym są podstawowe pojęcia logiczne.
Skrypt niniejszy zawiera elementy logiki klasycznej w zakresie zapewniającym czytelnikowi uświadomienie roli logiki w zakresie wnioskowania.
Autor starał się, aby wyłożony materiał stanowił pewną całość i został tak wyłożony, aby czytelnik w zakresie zrozumienia podstawowych pojęć logiki nie musiał odwoływać się do literatury. Nie mniej jednak osoby pragnące poszerzyć zakres swojej wiedzy logicznej mogą sięgnąć do przedstawionej na końcu wykładu literatury.
Skrypt podzielony jest na sześć wykładów. Każdy wykład następny z reguły zawiera niektóre pojęcia sformułowane w wykładach wcześniejszych. I w takim porządku należy z tego skryptu korzystać.
Na zakończenie tego wstępu autor chciałby podkreślić, że wykład obejmuje pojęcia uchodzące dziś już za klasyczne. Metoda wykładu również jest jak klasyczna. Wydaje się, ze właśnie klasyczna metoda wykładu umożliwia przedstawienie problematyki logicznej w sposób najbardziej przystępny.
Klasyczny rachunek zdań
Logika uchwytuje sposoby wnioskowania stosowane w naukach i uznawane za poprawne oraz tworzy z nich systemy logiczne. Systemy te są zbiorem praw i reguł, do których stosując się można odtworzyć te wszystkie wnioskowania, które spontanicznie uznajemy za bez zarzutu.
Logika, pojęta jako nauka odnosząca się do wnioskowania, obejmuje trzy dyscypliny, które powinny być ściśle oddzielane.
Logika formalna - rozważa tzw. prawa logiczne, tzn. zdania, „według których” musi się wnioskować, jeśli chce się od jednych zdań prawdziwych dojść do innych zdań prawdziwych.
Metodologia - jest teorią zastosowania praw logiki do różnych dziedzin.
Filozofia logiki - stawia pytania dotyczące samej logiki i natury jej praw.
Dział metodologii, którego przedmiotem badań jest nauka pojęta jako rzemiosło uczonych, tj. nauka pojęta jako czynność nazywa się metodologią pragmatyczną (od greckiego pragma, czytaj „pragma”, co znaczy to samo, co polskie „czyn”).
K. Ajdukiewicz, Logika pragmatyczna, PWN, W-wa, 1969, str. 175.
Podstawowe pojęcia logiczne
Pojęcie zdania w sensie logicznym
Zdanie w sensie logicznym jest to wyrażenie jednoznacznie stwierdzające, na gruncie reguł danego języka, iż tak a tak jest, albo że tak a tak nie jest.
Wartość logiczna zdania
Zdanie prawdziwe jest to zdanie, które opisuje rzeczywistość taką, jaka ona jest.
Zdanie fałszywe jest to zdanie, które opisuje rzeczywistość niezgodnie z tym, jak się ona ma.
Prawdziwość zdania albo jego fałszywość nazywamy wartościami logicznymi zdania.
Wartość logiczna zdania jest czymś obiektywnym, to znaczy nie zależy od poglądów tej czy innej osoby. Od tego, czy ktoś dane zdanie uważa za prawdziwe, czy fałszywe, nie zmienia się wartość logiczna zdania.
Funkcje zdaniowe
Funkcją zdaniową (formułą zdaniową) nazywa się w logice wyrażenie opisowe, które zawiera zmienne. Wyrażenie takie po dokonaniu odpowiednich podstawień na miejsce zmiennych staje się zdaniem w sensie logicznym.
Przykład:
„Jeżeli p, to q” - funkcja zdaniowa
p - „20 dzieli się przez 10” - zdanie
q- „20 dzieli się przez 2” - zdanie
Jeżeli (20 dzieli się przez 10), to (20 dzieli się przez 2) -zdanie prawdziwe.
Język rachunku zdań
Zmienne zdaniowe
p, q, r, s, t, u, w, …
oznaczamy literami z końca alfabetu
Spójniki zdaniowe (funktory prawdziwościowe);
~, →, ∧, ∨, ≡, (oznaczenia)
~ - negacja
→ - implikacja
∧ - koniunkcja
∨ - alternatywa
≡ - równoważność
p ∨ q czytamy p lub q
p ∧ q czytamy p i q
p → q czytamy jeśli p, to q
p ≡ q czytamy p wtedy i tylko wtedy, gdy q
~ p czytamy nieprawda, że p
Schematy zdań złożonych
Formę zdaniową rachunku zdań zawierającą zmienne zdaniowe nazywamy schematem zdania złożonego. Zdania podpadające pod schemat, to wszystkie zdania utworzone ze schematu przez dowolne podstawienia zdań pod zmienne zdaniowe.
Logika zbudowana ze zmiennych i 5 spójników zdaniowych (funktorów) oraz dodatkowo nawiasów (), [], {} nazywa się często logiką Arystotelesa.
W logice Arystotelesa funktory definiuje się następująco (za pomocą matryc):
Matryce logiczne funktorów
prawda logiczna - stała 1,
fałsz logiczny - stała 0
p |
~ p |
0 |
1 |
1 |
0 |
p |
q |
p ∨ q |
|
p |
q |
p ∧ q |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
p |
q |
p → q |
|
p |
q |
p ≡ q |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
Wartość logiczna zdania złożonego zależy jedynie od wartości logicznych zdań składowych.
Np. [(p ≡ q) ∧ (~ p ∨ q)] ∨ ~ (p → q)
{ (p ≡ q), (~ p ∨ q), ~ (p → q)}- składowe.
Tak zbudowana logika nazywa się klasycznym rachunkiem zdań (skrótowo pisać będziemy k.r.z.). K.r.z. zawiera tylko trzy rodzaje wyrażeń logicznych (funkcji zdaniowych), tak zwane tautologie, wyrażenia spełniane oraz antytautologie. Wszystkie wyrażenia logiczne (sensownie zbudowane) k.r.z. są skończone, tzn. składają się ze skończonej liczby zmiennych i funktorów logicznych.
Warto zauważyć, że wszystkie wyrażenia, które definiują podstawowe funktory k.r.z. są wyrażeniami spełnialnymi, tzn. dla niektórych wartościowań ich zmiennych są prawdzie, a dla niektórych - fałszywe. Antytautologie są zaprzeczeniem tautologii i są zawsze fałszywe, a tautologie zawsze prawdziwe.
Uwaga: często całe wyrażenie, aby nie podawać jego postaci (budowy) oznacza się literami alfabetu greckiego: a, b, g, j, itd.
Tautologie klasycznego rachunku zdań
Ważną rolę w poprawnym wnioskowaniu odgrywają takie schematy zdań złożonych, że każde zdanie podpadające pod taki schemat jest zawsze zdaniem złożonym prawdziwym. Schematy takie zwiemy tautologiami klasycznego rachunku zdań lub po prostu twierdzeniami (prawami) klasycznego rachunku zdań.
Jako przykład tautologii klasycznego rachunku zdań służyć może schemat:
p ∨ ~ p,
zwany prawem wyłącznego środka.
Przykładami zdań o tym schemacie są np.:
Dla dowolnej liczby rzeczywistej x:
x = 0 lub x ≠ 0,
x jest liczbą wymierną, lub x nie jest liczbą wymierną.
Dowolne dwie proste na płaszczyźnie są równoległe, lub dowolne dwie proste na płaszczyźnie nie są równoległe.
Tautologią jest też schemat:
(p → q) → (~ q → ~ p),
zwany prawem transpozycji.
Przykład zdania podpadającego pod powyższy schemat:
Jeżeli [(znam język francuski), (to mogę czytać Molliera w oryginale)], to [jeżeli (czytam utwory Molliera w oryginale i nie rozumiem ich treści), to (nie znam języka francuskiego)].
Innym przykładem tautologii jest schemat:
p → ~ ~ p
nazywany prawem podwójnego przeczenia.
Wspomniano, że tautologie (wyrażenia logiczne zawsze prawdziwe, przy dowolnym wartościowaniu zmiennych zdaniowych) odgrywają szczególną rolę w k.r.z., więc powstaje pytanie, jak sprawdzić prawdziwość dowolnych wyrażeń logicznych.
O tautologiach można mianowicie dowieść następującego twierdzenia (o rozstrzygalności k.r.z.).
Istnieje efektywna metoda (algorytm), pozwalająca sprawdzić w skończonej liczbie kroków, czy dowolny schemat a zbudowany ze spójników i zmiennych zdaniowych (liter) oraz nawiasów jest prawem (tautologią) k.r.z., czy też nią nie jest.
Metodę tę nazywa się powszechnie metodą sprawdzania zero - jedynkowego. Sposób jej stosowania jest bardzo prosty. Każdą zmienną w dowolnym schemacie a reprezentuje jakieś zdanie prawdziwe bądź fałszywe: zmienną należy więc w schemacie a zastąpić raz symbolem 0, a drugi raz symbolem 1. Postępując w ten sposób z każdą zmienną, otrzymujemy w schemacie pewną liczbę konkretnych podstawień. Liczba tych podstawień jest skończona.
Dla n zmiennych mamy 2n podstawień.
Przykład: niech wyrażenie a ma postać:
α = [(p → q) → [(q → r) → (p → r)].
Sprawdzić (metodą matrycową) czy wyrażenie a może stanowić w logice schemat wnioskowania budując tablicę zawierającą wszystkie zmienne i elementy składowe.
Tablica prawdziwościowa:
p
|
q |
r |
p → q |
q → r |
p → r |
(q → r) → (p → r) |
a |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
n = 3 23 = 8 - kombinacji podstawień
a - jest tautologii
Jest to jedno z pierwszych znanych już w starożytnej Grecji praw, które nazywa się prawem sylogizmu warunkowego stoików.
Inną wersję tego prawa podaje się w postaci:
[(p → q) ∧ (q → r)] → (p →r)]
Jeżeli z p wynika q, a r wynika z q, to r wynika też z p.
Przykład. Jeżeli dziś jest poniedziałek, to jutro jest wtorek i jeżeli jutro jest wtorek, to pojutrze jest środa, to jeżeli dziś jest poniedziałek, to pojutrze jest środa.
Metoda skrócona
Jeżeli wyrażenie logiczne dane jest w postaci implikacji, to tautologiczność (prawdziwość) takiego wyrażenia można sprawdzić tzw. metodą skróconą. Sprawdzamy tylko te podstawienia, przy których implikacja może być fałszywa, czyli następnik fałszywy a poprzednik prawdziwy( zgodnie definicją implikacji).
Przykład. Weźmy ponownie wyrażenie:
a = (p → q) → [(q → r) → (p → r)]
Aby a było równe zero, (p → q) musi być równe 1 i [(q → r) → (p → r)] = 0. Aby [(q → r) → (p → r)] = 0 , to [(q → r) = 1, a (p → r) = 0. Aby (p→r)=0 musi być p = 1, r = 0, a więc tylko przy tym podstawieniu formuła może być fałszywa (równać się 0). Szukamy jeszcze warunku dla zdania q. Skoro (q → r) musi być równe 1, a r = 0, to q musi być równe zeru, bo inaczej (q → r) nie byłoby równe 1. A więc tylko przypadek, gdy p = 1, r = 0, q = 0 może być tym, przy którym formuła jest równa 0. Patrząc na poprzednio przytoczoną macierz, widzimy, że i przy tym wartościowaniu a przyjmuje też wartość 1. A więc a jest tautologią.
Zadania. Sprawdzić tautologiczność następujących wyrażeń (metodą matrycową i skróconą):
1. (p → q) → (~ p ∨ q)
2. (~ p → p) → ~ p
3. (p → ~ p) → p
4. ~ ~ p → p
5. (p → ~ q) → (q → ~ p)
6. [(p → q) ∧ ~ q] → ~ p
7. [p → (q ∧ ~ q)] → ~ p
8. [p → (q→ r) → (p ∧ q) → r
9. [(p ∧ q) → r] → [(p → (q → r)]
10. [p → (q → r)] → [q → (p → r)]
11. [(p → r) ∧ (q → r)] → [(p ∨ q) → r]
12. [(p → q) ∧ (p → r)] → [(p → q ∧ r)]
13. p → (q → p)
14. (p ∨ q) → (~ p → q)
15. ~ (p ∨ q) ≡ ~ p ∧ ~ q
16. ~ (p ∧ q) ≡ ~ p ∨ ~ q
Podać też treściowe przykłady z życia potocznego dla niektórych z tych praw.
Normalna postać koniunkcyjno - alternatywna
Wyrażenie α jest w postaci normalnej koniunkcyjno - alternatywnej a' wtedy i tylko wtedy, gdy jest koniunkcją pewnej liczby alternatyw a1, a2, a3, …, an, przy czym członami alternatyw są zmienne zdaniowe lub negacje zmiennych zdaniowych:
Twierdzenie. Jeśli a jest w postaci normalnej koniunkcyjno - alternatywnej i a jest koniunkcją alternatyw a1, a2, a3, …, an, to a jest tautologią wtedy i tylko wtedy, gdy w każdej alternatywie a1, a2, a3, …, an , pewna zmienna występuje bez negacji i z negacją.
a' = (p ∨ q ∨ …~ p ∨ ~ r) ∧ …∧ (p ∨ ~ s ∨ …).
a1 = (p ∨ q ∨ …~ p ∨ ~ r), …, an = (p ∨ ~ s ∨ …).
Przykłady.
Formuła w postaci n.k.a. |
Tautologia? |
(p ∨ ~ p) ∧ (q ∨ r ∨ ~ q) |
tak |
(p ∨ q ∨ ~ p) ∧ (q ∨ ~ r) |
nie |
P ∨ ~ q ∨ r ∨ ~ p |
tak |
(p ∨ ~ q) ∧ (~ p ∨ q) |
nie |
Sprowadzanie do normalnej postaci k.a.
Usunąć z wyrażenia wszystkie równoważności stosując
(p ≡ q) ≡ [(p → q) ∧ (q → p)].
Usunąć z wyrażenia wszystkie implikacje stosując (p → q) ≡ (~ p ∨ q).
Dopóki można, to:
* upraszczać stosując (p ∨ p) ≡ p oraz (p ∧ p) ≡ p.
* usuwać zbędne negacje stosując prawo podwójnego przeczenia
~ ~ p ≡ p.
* stosować prawa de Morgana:
~ (p ∨ q) ≡ (~ p ∧ ~ q)
~ (p ∧ q) ≡ (~ p ∨ ~ q).
* stosować prawo rozłączności alternatywy względem koniunkcji:
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r).
Najczęściej stosowanymi prawami w otrzymywaniu z wyrażenia a jej postaci normalnej k.a. a' są zatem:
(p ≡ q) ≡ (p → q) ∧ (q → p)
(p → q) ≡ ~ p ∨ q
~ ~ p ≡ p
p ∨ q ≡ q ∨ p
p ∧ q ≡ q ∧p
p ∨ p ≡ p
p ∧ p ≡ p
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
~ (p ∨ q) ≡ ~ p ∧ ~ q
~ (p ∧ q) ≡ ~ p ∨ ~ q
p ∨ q ∨ r ≡ (p ∨ q) ∨ r ≡ p ∨ (q ∧ r)
p ∧ q ∧ r ≡ p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r
Proste przykłady stosowania praw w doprowadzaniu wyrażeń logicznych do postaci n.k.a.:
Czy (p → ~ p) → ~ p jest tautologią?
(p → ~ p ) → ~ p
~ (p → ~ p) ∨ ~ p
~ (~ p ∨ ~ p) ∨ ~ p
~ ~ p ∨ ~ p
p ∨ ~ p - tautologia
Czy (p ∧ ~ p) → q jest tautologią?
(p ∧ ~ p) → q
~ (p ∧ ~p) ∨ q
~ p ∨ ~ ~ p ∨ q
(~ p ∨ p ∨ q)- tautologia.
Czy (p → q) → ((p ∧ r) → (q ∧ r)) jest tautologią?
1. (p → q) → ((p ∧ r) → (q ∧ r))
2. ~ (p → q) ∨ ((p ∧ r) → (q ∧ r))
3. ~ (p → q) ∨ ~ (p ∧ r) ∨ (q ∧ r)
4. ~ (~ p ∨ q) ∨ ~ (p ∧ r) ∨ (q ∧ r)
5. (~ ~ p ∧ ~ q) ∨ ~ (p ∧ r) ∨ (q ∧ r)
6. (p ∧ ~ q) ∨ ~ (p ∧ r) ∨ (q ∧ r)
7. ((p ∧ ~ q) ∨ (~ p ∨ ~ r) ∨ (q ∧ r)
8. ((p ∧ ~ q) ∨ (~ p ∨ ~ r ∨ q)) ∧ ((p ∧ ~ q) ∨ (~ p ∨ ~ r ∨ r ))
9. (p ∨ ~ p ∨ ~ r ∨ q) ∧ (~ q ∨ ~ p ∨ ~ r ∨ q) ∧ ((p ∧ ~ q) ∨ (~ p ∨ ~ r ∨ r))
10. (p ∨ ~ p ∨ ~ r ∨ q) ∧ (~ q ∨ ~ p ∨ ~ r ∨ q) ∧
∧ (p ∨ ~ p ∨ ~ r ∨ r) ∧ (~ q ∨ ~ p ∨ ~ r ∨ r)
Uwaga. Podkreślony funktor lub wyrażenie zawierające funktor oznacza, że funktor ten na podstawie odpowiedniego prawa będzie przekształcony i inna postać. Nową postać zawiera następny krok (numer) procedury doprowadzania do postaci normalnej.
Zadania.
Doprowadzić do postaci normalnej k.a. poniższe wyrażenia i rozstrzygnąć bez sprawdzania metodą matrycową lub skróconą, które z nich są tautologiami, a które tautologiami nie są:
1. p → (q → p)
2. p → (q → r) → q → (p → r)
3. [(p → q) → p] → p
4. [(p ∧ q) → r)] → p → (q → r)
5. [p ∧ (q ∨ r)] → [(p ∧ q) ∨ (p ∧ r)]
6. [(p → q) ∧ ~ q] → ~ p
7. [(p → q) ∧ p] → q
8. (p → q) → [(p ∧ r) → q]
9. [(p → q) ∧ (q → p)] → (p ∨ q)
10. p → [~ p ∨ q]
Rachunek zdań jako system aksjomatyczny
Klasyczny rachunek zdań ujmowany był dotychczas w sposób syntetyczny, podając w twierdzeniu o rozstrzygalności łatwą metodę konstrukcji za pomocą spójników, zmiennych zdaniowych i nawiasów, dowolnej liczby praw tego rachunku. Zwykle jednak teorie dziedzin nauki - szczególnie teorie matematyki, powstają nieco inaczej. Tworzone są w sposób aksjomatyczny.
Aksjomaty klasycznego rachunku zdań
W każdym aksjomatycznym ujęciu pewnych teorii bierze się pod uwagę podstawowe własności przedmiotów rozważanych w tych teoriach. Na ogół są to własności najbardziej oczywiste, pewne. Stąd zdania wyrażające te własności zwie się pewnikami lub aksjomatami teorii.
Wszelkie inne twierdzenia teorii wyprowadza się z aksjomatów drogą logicznego wnioskowania. Wobec tego samym systemom logicznym również można nadać tego typu aksjomatyczną budowę.
W odniesieniu do klasycznego rachunku zdań istnieje bardzo wiele różnych układów aksjomatów równoważnych między sobą. Omówiony zostanie jeden z tych układów zwany aksjomatyką J. Łukasiewicza.
Pojęcie teorii
Sprowadzenie jakiejś teorii T (dziedziny wiedzy) do takiego wyglądu, że każde do tej pory otrzymane twierdzenie teorii T jest albo jej aksjomatem, albo zostało uzyskane z aksjomatów teorii T przez zastosowanie pewną liczbę razy reguł wnioskowania, zwie się formalizacją teorii T.
Konsekwencją (wnioskiem) pewnego zbioru X jest każde zdanie, które można dowieść w oparciu o zbiór X, czyli wyprowadzić z pewnej skończonej liczby zdań zbioru X, posługując się regułami wnioskowania.
Teorią zaś jest każdy taki zbiór zdań X, który ma te własności, że wnioski z teorii należą nadal do zbioru X.
Twierdzenie. Teoria jest zbiorem zamkniętym ze względu na swoje konsekwencje.
Można powiedzieć inaczej, że zbiór X jest teorią wtedy i tylko wtedy, gdy jest identyczny ze zbiorem swych konsekwencji, czyli gdy zachodzi
X = Cnq (X)
Cnq(X) - konsekwencja zbioru X.
Twierdzenie. Zbiór tautologii k.r.z. jest teorią.
Reguły wnioskowania.
K.r.z. posługuje się dwoma regułami wnioskowania, regułami dowodowymi. Umożliwiają one wyprowadzanie z praw danych innych dowolnych praw. Są nimi:
Reguła odrywania.
Reguła podstawiania.
Definicja (Reguła odrywania). Jeśli uznajemy pewien schemat będący implikacją a → b za prawo logiki oraz uznajemy za prawo logiki schemat a będący poprzednikiem schematu pierwszego, to za prawo logiki musimy też uznać schemat b będący następnikiem schematu pierwszego.
Definicja (Reguła podstawiania). Za prawo logiki musimy uznać wszystkie schematy, które są szczególnymi przypadkami schematów uznanych za prawa logiki.
Przykład 1. Jeśli uznajemy za prawo logiki schemat
p → (q → p) (prawo symplifikacji)
oraz uznajemy za prawo logiki schemat
(p → (q → p)) → ((p → q) → (p → p)),
To musimy uznać, zgodnie z regułą odrywania, za prawo wyrażenie
(p → q) → (p → p).
Przykład 2. Jeśli za prawo logiki uznajemy prawo wyłączonego środka p ∨ ~ p, to musimy uznać za prawo logiki wyrażenie
(p → q) ∨ ~ (p → q),
które powstaje z niego przez podstawienie p/(p → q), jak również formułę
(p → (q ∧ r)) ∨ ~ (p → (q ∧ r)),
która powstaje z poprzedniej tautologii przez podstawienie q/(q ∧ r), (czytaj q/(q ∧ r) - za q podstaw (q ∧ r)).
Własności klasycznego rachunku zdań
Własności te wynikają z ostatniego twierdzenia:
Każdy schemat będący podstawieniem tautologii jest tautologią.
Schemat powstały przez odrywanie z dwóch tautologii jest również tautologią.
Własność 1. wynika z definicji podstawienia, a zwłaszcza z własności tautologii (zawsze prawdziwa). Własność 2. łatwo jest udowodnić.
Przypuśćmy, że schemat a i a → b są tautologiami k.r.z. Gdyby b nie było tautologią, to istniałoby takie podstawienie, że b jest fałszywe. Dokonajmy tego podstawienia w całym schemacie a → b. Skoro a jest tautologią, to przy tym podstawieniu, a przechodzi w zdanie prawdziwe. Otrzymujemy więc, że
1 → 0,
a to oznacza, że a → b nie jest tautologią, co przeczy założeniu, że schemat a → b jest tautologią, czyli b musi być tautologią. Reguła odrywania nie wyprowadza więc poza tautologie.
Definicja. Zbiór Y jest skończenie aksjomatyzowalny wtedy i tylko wtedy, gdy istnieje taki skończony zbiór X, że
Y = Cnq (X).
Twierdzenie. Zbiór tautologii k.r.z. jest skończenie aksjomatyzowalny.
Dowód (szkic). Każdą formułę, będącą schematem zdaniowym, można równoważnościowo sprowadzić do postaci normalnej. Sprowadzenie tego, jak już wiemy, dokonać można za pomocą pewnej skończonej liczby twierdzeń (praw logiki). Jeżeli wyrażenie mające postać normalną jest tautologią, to wynika też ono z pewnej liczby explicite wypisanych tautologii. Ponadto zachodzi równoważność tautologii a i jej postaci normalnej. A więc jeżeli a jest tautologią, to a' też jest tautologią i a ≡ a'. Równoważność a ≡ a' jest tautologią, ponieważ powstaje z tautologii, a zbiór tautologii k.r.z. jest teorią. Stąd jeżeli a jest tautologią, to a' musi być tautologią. Ale skoro a' jest tautologią, to a jest konsekwencją powyższej skończonej liczby twierdzeń. Zbiór tautologii jest więc skończenie aksjomatyzowalny (A. Grzegorczyk, Zarys logiki matematycznej, PWN, Warszawa, 1969, str. 101-105).
Aksjomatyka
Terminy (pojęcia) pierwotne:
~ , →
Aksjomaty:
A1: (p → q) → [(q → r) → (p → r)]
A2: p → (~ p → q)
A3: (~ p → p) → ~ p.
A1 - prawo sylogizmu warunkowego stoików
A2 - prawo Dunsa Scotusa
A3 - prawo Claviusa.
Przyjęte aksjomaty, zbudowane z pojęć pierwotnych, nie zawierają funktorów ∨, ∧, i ≡. Należy więc je zdefiniować za pomocą przyjętych pojęć pierwotnych.
Definicje:
d1. p ∨ q ![]()
~ p → q
d2. p ∧ q ![]()
~ (p → ~ q)
d3. p ≡ q ![]()
(p → q) ∧ (q → p).
Uwaga. W definicji równoważności posłużono się koniunkcją, gdyż została ona już wcześniej zdefiniowana.
W powyższym systemie aksjomatycznym przyjmuje się ponadto osobną dyrektywę, mówiącą o stosowaniu definicji, która brzmi:
W dowolnym twierdzeniu k.r.z. można dowolną część równokształtną z jedną ze stron definicji zastąpić przez część równokształtną z drugą ze stron tejże definicji.
Dyrektywa ta zwie się dyrektywą zastępowania definicyjnego. Stosując ją np. do aksjomatu A2, otrzymujemy z niego twierdzenie
T: p → (p ∨ q),
Zastępując wyrażenie (~ p → q) w A2 lewą stroną definicji d1.
Zbiór konsekwencji trzech wymienionych wyżej aksjomatów przy dołączeniu do reguł (pierwotnych) logicznych podstawiania i odrywania jeszcze reguły zastępowania definicyjnego, jest identyczny z klasycznym rachunkiem zdań.
Układ aksjomatów powinien być niezależny, niesprzeczny i zupełny. Aksjomaty powinny być niezależne, tzn. układ aksjomatów, w którym żaden nie wynika z pozostałych, nazywa się niezależnym układem aksjomatów.
Układ aksjomatów powinien być niesprzeczny, tzn. w systemie nie mogą być jednocześnie twierdzeniami dwa wyrażenia sprzeczne. Czyli, jeżeli A jest twierdzeniem prawdziwym, to ~ A musi być fałszywe.
Zupełność oznacza, że wzbogacając system aksjomatów jakimkolwiek wyrażeniem nie będącym twierdzeniem, otrzymujemy system sprzeczny. Mówimy też, że teoria jest pełna, jeśli każde prawdziwe zdanie w tej teorii da się udowodnić na podstawie aksjomatów wedle reguł dowodzenia w niej obowiązujących.
Twierdzenie o zupełności i pełności
Twierdzenie. Zbiór tautologii klasycznego rachunku zdań jest teorią zupełną i pełną.
W powyższy sposób sformułowane systemy logiczne nazywa się systemami dedukcyjnymi. Najważniejszą cechą systemów dedukcyjnych jest ich niesprzeczność. Pełność systemu oznacza, że każde wyrażenie prawdziwe rachunku zdań jest jego konsekwencją, czyli zostało udowodnione.
Jak zatem należy formalnie rozumieć dowód dowolnej konsekwencji.
Definicja. D jest dowodem zdania B w oparciu o zbiór reguł X przyjętych jako założenia wtedy i tylko wtedy, gdy D jest skończonym ciągiem formuł.
D = {D1, D2, …, Dn}
takim, że ostatnia formuła tego ciągu jest identyczna ze zdaniem B: Dn = B, oraz każda formuła Dk ciągu D (1 ≤ k ≤ n) 1° albo należy do zbioru X, 2° albo powstaje z pewnej formuły Dj tego ciągu wcześniejszej od Dk (j < k) przez prawidłowe podstawienie, 3° albo powstaje z pewnych dwóch formuł ciągu A: Dj, Di wcześniejszych od Dk (j < k, i < k) przez odrywanie: Dj = (Di → Dk).
Zatem na dowód każdego twierdzenia w logice składa się pewna skończona liczba innych już udowodnionych twierdzeń oraz reguła podstawiania i odrywania.
Przykłady dowodów twierdzeń wynikających bezpośrednio z aksjomatu k.r.z.
Przykład 1. Pokazać, że tautologia
p → p
daje się bezpośrednio wyprowadzić (udowodnić) z aksjomatu A1, A2, i A3.
Dowód. Mamy dane aksjomaty
A1: (p → q) → [(q → r) → (p → r)],
A2: p → (~ p → q),
A3: (~ p → p) → p.
W A1 za q podstawiamy (~ p → q), czyli q/(~ p → q).
Otrzymujemy
[p → (~ p → q) → {[(~ p → q) → r ] → (p → r)] stosując do tej tezy i A2 regułę odrywania (RO) otrzymujemy
[(~ p → q) → r} → (p → r).
Następnie podstawiamy w 2. q / p i p / r. Mamy
[(~ p → p) → p] → (p → p).
Stosując do 3. i A3 regułę RO otrzymujemy podane twierdzenie, czyli
p → p.
Przykład 2. W praktyce nie wszystkie twierdzenia k.r.z. wynikają bezpośrednio z aksjomatów, lecz wiele z nich wynika bezpośrednio z innych twierdzeń, które uważa się za wyprowadzone, albo bezpośrednio z aksjomatów, albo wynikają one bezpośrednio z innych twierdzeń.
Możemy zapytać, z jakich twierdzeń logiki wynika bezpośrednio twierdzenie:
T: (p → q) ∧ (q → r) → (p → r).
Za jedno z twierdzeń bierzemy aksjomat A1, czyli
0. (p → q) → [(q →r) → (p → r)]
oraz prawo, które uważamy za udowodnione
p → (q → r) → (p ∧ q) → r.
W tautologii 1. w miejsce p, q i r podstawiamy:
p/(p → q), q/(q → r), r/(p → r).
Otrzymujemy
2. {(p → q) → [(q → r) → (p → r)]} → {[(p → q) ∧ (q v r)] → (p → r)}
Stosując do prawa 2. i aksjomatu A1 regułę odrywania otrzymujemy żądane twierdzenie
(p → q) ∧ (q → r) → (p → r).
Wspomniano, że k.r.z. został zaksjomatyzowany na wiele różnych sposobów. Poniżej podany zostanie przykład innej aksjomatyki, w której jest znacznie większa liczba aksjomatów, niż poprzednio.
Przykład innej aksjomatyki:
1. pojęcia pierwotne
~, ∧, ∨, →, ≡.
Aksjomaty.
Aksjomaty pozytywne implikacji:
p → (q → p),
(p → (q → r)) → ((p → q) → (p → r)).
Aksjomaty charakteryzujące równoważność za pomocą implikacji:
(p ≡ q) → (p → q),
(p ≡ q) → (q → p),
(p → q) → ((q → p) → (p ≡ q)).
Aksjomaty charakteryzujące koniunkcję i alternatywę:
(p ∨ q) → (q ∨ p)(p ∧ q) → (q ∧ p) przemienność
p → (p ∨ q)( p ∧ q) → p pochłanianie
p → (q → (p ∧ q)) łączenie znakiem koniunkcji
((p → r) ∧ (q → r)) → ((p ∨ q) → r) łączenie znakiem
alternatywy
Prawa charakteryzujące negację
(→ (q ∧ ~ q)) → ~ p
(p ∧ ~ p) → q
Prawo wyłącznego środka
p ∨ ~ p
Aksjomaty 1-11 stanowią aksjomatykę tzw. logiki pozytywnej. Logika pozytywna nie zawiera twierdzeń dotyczących negacji. Aksjomaty 1-13 stanowią logikę intuicjonistyczną. Logika intuicjonistyczna nie zawiera prawa wyłącznego środka. Są to systemy logiki węższe w stosunku do k.r.z.
Logika intuicjonistyczna
Intuicjonizm odrzuca pewne reguły wnioskowania logiki klasycznej, które powodują, że na przykład dowody istnienia pewnych obiektów nie podają żadnego sposobu na skonstruowanie tych obiektów. Dla przykładu kwestionowane jest prawo wyłącznego środka p ∨ ~ p.
Twierdzenie. Istnieją liczby niewymierne a, b ∈ R, takie że ab jest liczbą wymierną.
Dowód. Jeżeli ![]()
jest liczbą wymierną, to bierzemy a = b = ![]()
. Jeśli natomiast ![]()
jest liczbą niewymierną, to bierzemy a = ![]()
oraz b = ![]()
. Wówczas
(![]()
)![]()
= ![]()
= 2.
To kończy dowód twierdzenia.
Powyższy dowód nie jest konstruktywny. Skorzystano w nim z prawa wyłącznego środka: ![]()
jest wymierne lub nie jest.
Zadania.
1. Z jakiego prawa można bezpośrednio otrzymać tezę:
T: (q → r) → [p → (q → r)].
Wskazówka. Zauważmy, że teza ta ma następującą budowę (schemat):
a → (b → g),
Należy więc wziąć tautologię, która będzie tak zbudowana, a następnie należy dokonać odpowiednich podstawień, czyli skorzystać z odpowiednich tautologii i odpowiednich podstawień.
2.Pokazać, że tezę o postaci
T: [(q → p) → r] → (p → r)
można bezpośrednio otrzymać z następujących tautologii:
p → (q → p)
(p → (q → p) → {[(q → p) → r] → (p → r)] → (p → r)}.
3. Jaka tautologia wynika bezpośrednio z praw:
p → p
(r → r) → {[r → (r → q)] → (r → q)].
4. Pokazać, że z prawa
(p → q) → [( q → r) → (p → r)]
można wyprowadzić prawo:
(q → r) → [(p → q) → (p → r)].
Wskazówka. Przyjąć takie prawo, w którym przez odpowiednie podstawienie w poprzedniku otrzyma się 1., a w następniku 2. Przez zastosowanie RO do prawa 2.
Metoda założeniowa
Aksjomatyczne ujęcie rachunku zdań polegało na tym, że obracaliśmy się tylko i wyłącznie w obszarze tautologii. W wielu sytuacjach, zdarzeniach, procesach rzeczywistych na strukturę logiczną tych procesów składają się elementy logiczne, które tautologiami nie są. Powstaje pytanie, jak w takich przypadkach wykazywać, że jednak proces jako całość tworzy twierdzenie logiki, czyli tautologię. Można ogólnie powiedzieć, że w rozumowaniach potocznych posługujemy się elementami logicznymi, które osobno wzięte nie muszą tworzyć twierdzeń logiki. Tworzone dla takiego rozumowania systemy nazywają się systemami dedukcji naturalnej. W systemach tych formułuje się dokładnie reguły, według których - w sposób intuicyjny - przeprowadzamy nasze dowody. Ponadto dowody w systemach założeniowych są na ogół łatwiejsze od dowodów w aksjomatycznych systemach logicznych.
Reguły systemu założeniowego określają, jak zbudowane są dowody założeniowe. Wśród reguł tworzących dowody założeniowe można wyróżnić dwa rodzaje reguł:
reguły dołączania nowych wierszy do dowodu,
reguły tworzenia dowodów.
Reguły typu 1. stwierdzają, że z wyrażeń o określonej postaci wynikają logicznie wyrażenia o określonej postaci, które można do dowodu dołączyć na podstawie wierszy dotychczasowych. Istnieje niewielka ilość takich reguł, które przyjmuje się bez dowodu, jako reguły pierwotne (zapisane w postaci schematów).
Reguły pierwotne
1. Reguła odrywania (RO) stwierdza, że z danej implikacji i prawdziwości jej poprzednika, wynika prawdziwość jej następnika. W myśl tej reguły schemat
p → q
p
q
jest schematem logicznym.
Jeśli więc do dowodu należy implikacja i jej poprzednik, to do dowodu, jako nowy wiersz wolno dołączyć jej następnik.
Przykład.
Jeżeli miasto x jest stolicą danego państwa y, to prezydent tego państwa rezyduje w mieście x.
Miasto x jest stolicą państwa y.
Prezydent państwa y rezyduje w mieście x
Reguła dołączania koniunkcji (DK). Jeżeli osobno zachodzi p i osobno zachodzi q, to zachodzi też p ∧ q.
p
q
p ∧ q
jest schematem logicznym.
Przykład.
Mickiewicz jest autorem „Pana Tadeusza”.
Mickiewicz jest autorem „Grażyny”
Mickiewicz jest autorem „Pana Tadeusza” i Mickiewicz jest autorem „Grażyny”
3. Reguła opuszczania koniunkcji (OK)
p ∧ q p ∧ q
p q
Są to schematy logiczne.
4. Reguła dołączenia alternatywy (DA), stwierdza, że z dowolnego zdania wynika alternatywa.
p q
p ∨ q p ∨q
W myśl tej reguły powyższe schematy są schematami logicznymi.
5. Reguła opuszczania alternatywy (OA) stwierdza, że z alternatywy i negacji jednego z jej członów wynika drugi jej człon. W myśl tej reguły schematy opuszczania alternatywy:
p ∨ q p ∨ q
~ p ~ q
q p
są schematami logicznymi.
Przykład.
Kontakt jest zepsuty lub żarówka jest spalona
Żarówka nie jest spalona
Kontakt jest zepsuty
6. Reguła dołączania równoważności (DE), stwierdza, że równoważność odpowiadająca danej implikacji wynika z tej implikacji i implikacji odwrotnej. W myśl tej reguły schemat dołączenia równoważności:
p → q
q →p
p ≡ q
jest schematem logicznym.
7. Reguła opuszczania równoważności (OR), stwierdza, że z danej równoważności wynika odpowiadająca jej implikacja oraz implikacja odwrotna.
W myśl tej reguły schematy opuszczania równoważności:
p ≡ q p ≡ q
p →q q → p
są schematami logicznymi.
Reguły tworzenia dowodu
Wprowadzimy obecnie pewną terminologię, z której będziemy korzystać przy formułowaniu reguł tworzenia dowodów założeniowych. Wyrażenia Φ1, Φ2, …, Φn-1 występujące w wyrażeniu:
(Φ) Φ1 → {Φ2 → [Φ3 → … → (Φn-1 → Φn) … ]}
nazywać będziemy poprzednikami Φn.
Dlaczego Φ1, Φ2, …, Φn-1 są poprzednikami Φn. Z budowy wyrażenia Φ można wnioskować, że równoważnym mu wyrażeniem jest Φ' o postaci:
(Φ') (Φ1 ∧ Φ2 ∧ … ∧ Φn-1) → Φn
W tym wyrażeniu Φn jest wyraźnie następnikiem i wnioskiem swoich poprzedników. Jeżeli Φ przedstawimy w postaci normalnej, to ma ono postać:
~ Φ1 ∨ ~ Φ2 ∨ … ∨ ~ Φn ∨ Φn ,
a postacią normalną wyrażenia Φ' jest
~ Φ1 ∨ ~ Φ2 ∨ … ∨ ~ Φn-1 ∨ Φn,
czyli obie formy są równoważne.
Na przykład elementy zbioru:
{p → q, q → r, p}
są poprzednikami wyrażenia
(p → q) → [(q → r) → (p → r)].
Jeżeli Φ1, Φ2, …, Φi są kolejnymi poprzednikami wyrażenia (Φ), to pozostałą część wyrażenia (Φ), a mianowicie wyrażenie:
Φi+1 → [… → (Φn-1 → Φn)],
będziemy nazywać następnikiem wyrażenia Φ odpowiadającym tym poprzednikom.
Na przykład w wyrażeniu:
(p → q) → [(q → r) → (p → r)]
poniższe
[(q → r) → (p → r)]
jest następnikiem odpowiadającym poprzednikowi (p → q), wyrażenie (p → r) jest następnikiem odpowiadającym poprzednikom (p → q) i (q → r), wyrażenie r jest następnikiem odpowiadającym poprzedni-kom: (p → q), (q → r), p.
Założeniowy dowód reguły stwierdzającej niezawodność danego schematu logicznego zaczynamy od wypisania założeń dowodu, którymi są przesłanki tego schematu oraz poprzedniki wniosku. Z tych założeń wyprowadzamy nowe wiersze według reguł dołączania nowych wierszy do dowodu (pierwotnych) lub uprzednio udowodnionych.
Możemy też do dowodu dołączyć jako nowe wiersze twierdzenia uprzednio udowodnione. Jest to opis założeniowego dowodu wprost (z.d.w.). Z.d.w. jest zakończony, gdy otrzymamy następnik wniosku odpowiadający tym poprzednikom wniosku, które są założeniami dowodu.
Przykładem jest dowód reguły sylogizmu warunkowego
p → q
q → r
p → r
W tym schemacie (p → q) i (q → r) są przesłankami, a (p → q), (q → r) i p stanowią poprzedniki wniosku r.
Dowód.
p → qq → r {założenia}
p
q (RO: 1, 3)
r (RO: 2, 4).
Uwaga. W dowodzie ostatniego wiersza nie numerujemy, zaznaczając w ten sposób, że dowód jest zakończony.
Założeniowy dowód twierdzenia zaczynamy od wypisania założeń twierdzenia, którymi są jego poprzedniki. Do dowodu dołączamy nowe wiersze według reguł dołączania nowych wierszy do dowodu (pierwotnych lub uprzednio udowodnionych) lub twierdzenia uprzednio udowodnione. Opisane wyżej postępowanie nazywamy założeniowym dowodem wprost. Dowód taki jest zakończony, gdy otrzymamy następnik tego twierdzenia odpowiadający tym jego poprzednikom, które występują jako założenia w dowodzie tego twierdzenia.
Założeniowy dowód wprost prawa (p → q) → [(q → r)→(p → r) pokrywa się z podanym powyżej dowodem reguły sylogizmu warunkowego.
Założeniowy dowód wprost jakiegoś twierdzenia odróżniamy od zwykłego dowodu wprost.
Zwykły dowód wprost jakiegoś twierdzenia rozpoczynamy od twierdzeń uprzednio udowodnionych. Z tych twierdzeń za pomocą reguł dołączenia nowych wierszy do dowodu wyprowadzamy - jako twierdzenie z nich wynikające - dowodzone twierdzenie.
W zwykłym dowodzie wprost każdy wiersz dowodu jest twierdzeniem (tezą), natomiast wiersze założeniowego dowodu, w szczególności założenia dowodu, nie muszą i często nie są tezami.
Przykładem zwykłego dowodu wprost będzie dowód prawa:
(p ∧ q) ≡ q ∧ p
Dowód. 1.) (p ∧ q) → (q ∧ p) {T 1}
2.) (q ∧ p) → (p ∧ q) {T 2}
(p ∧ q) ≡ (q ∧ p) {DE: 1, 2}
Wiersze 1.) i 2.) są tutaj twierdzeniami uprzednio udowodnionymi.
Założeniowy dowód nie wprost reguły stwierdzającej niezawodność danego schematu logicznego rozpoczynamy od wypisania założeń dowodu. Są nimi przesłanki tego schematu oraz poprzedniki wniosku. Wyrażenie sprzeczne z odpowiadającym mu następnikiem tego wniosku wypisujemy jako założenie dowodu nie wprost (z.d.n.). Przez wyrażenie sprzeczne rozumiemy tu jakieś wyrażenie Φ i jego negację ~ Φ. Wyrażenie dowodu nie wprost wypisujemy więc bądź poprzedzając dany następnik znakiem negacji bądź skreślając początkowy znak negacji w następniku o postaci ~ Φ. Do dowodu dołączamy nowe wiersze. Według reguł dołączania nowych wierszy do dowodu (pierwotnych lub uprzednio udowodnionych) lub twierdzenia uprzednio udowodnione. Założeniowy dowód nie wprost jest zakończony, gdy otrzymamy w nim dwa wiersze sprzeczne.
Tak samo zbudowany jest założeniowy dowód nie wprost jakiegoś twierdzenia, z tą jedynie różnicą, że założeniami dowodu są poprzedniki tego twierdzenia.
Przykłady założeniowych dowodów nie wprost:
~ p → q
~ q → p
Dowód. (1.) ~ p → q {zał.}
(2.) ~ q
(3.) ~ p {z.d.n}
(4.) q {RO: 1, 3}
Sprzeczność {2, 4}
p → q
~ q → ~ p
Dowód. (1.) ~ p → q {zał.}
(2.) ~ q
(3.) p {z.d.n}
(4.) q {RO: 1, 3}
Sprzeczność {2, 4}
Założenie dowodu nie wprost „p” powstaje tutaj z następnika wniosku „~ p” przez skreślenie w nim znaku negacji.
Uwaga. Przy zapisywaniu dowodów będziemy używać skrótów zał. zamiast „założenie”, z.d.n. zamiast „założenie dowodu nie wprost”, sprz. zamiast „sprzeczność”.
Zwykły dowód nie wprost jakiegoś twierdzenia tym tylko różni się od założeniowego dowodu nie wprost, że nie występują w nim założenia, a tylko założenie dowodu nie wprost. Założeniem dowodu nie wprost jest w takim dowodzie wyrażenie sprzeczne z dowodzonym twierdzeniem.
Oto przykład zwykłego dowodu nie wprost:
~ [(p → q) ∧ (p ∧ ~ q)]
Dowód. (1.) (p → q) ∧ (p ∧ ~ q) {z.d.n}
(2.) (p → q) { OK.:1}
(3.) (p ∧ ~ q)
(4.) p {OK.: 3}
(5.) ~ q
(6.) q {RO: 2, 4}
Sprz. {5, 6}
Zakończenie założeniowego lub zwykłego dowodu nie wprost zaznaczamy pisząc na końcu „sprz.” i podając po prawej stronie numery dwóch wierszy sprzecznych.
Uwaga. Każdy założeniowy dowód wprost reguły lub twierdzenia można przekształcić na założeniowy dowód nie wprost, wypisując po założeniach wyrażenie sprzeczne z następnikiem wniosku lub następnikiem dowodzonego twierdzenia (odpowiadającym tym poprzednikom, które są założeniami tego dowodu) jako założenie dowodu nie wprost.
Podobnie każdy zwykły dowód wprost można przekształcić na zwykły dowód nie wprost umieszczając na początku dowodu wyrażenie sprzeczne z dowodzonym twierdzeniem, jako założenie dowodu nie wprost.
Założeniowe dowody praw i reguł logicznych
Reguła sylogizmu warunkowego
p → q
q → r
p → r
Dowód był podany poprzednio.
Reguła modus tollens (toll.)
p → q ~ p → q p → ~ q ~ p → ~ q
~ q ~ q q q
~ p p ~ p p
Oto dowód pierwszego z nich
(1.) p → q {zał.}
(2.) ~ q
(3.) p {z.d.n.}
(4.) q {RO: 1, 3}
Sprz. {2, 4}
Reguła transpozycji (Transp.)
p → q ~ p → q p → ~ q ~ p → ~ q
~ q → ~ p ~ q → p q → ~ p q → p
Dowody były podane dla dwóch schematów, dla pozostałych są podobne.
Reguła transpozycji złożonej:
(r ∧ p) → q (r ∧ ~ p) → q (r ∧ p) → ~ q (r ∧ ~ p) → ~ q
(r ∧ ~ q) → ~ p (r ∧ ~ q) → p (r ∧ p) → ~ p (r ∧ q) → p
Dowód pierwszego ze schematów:
(1.) (r ∧ p) → q
(2.) r ∧ ~ q {zał.}
(3.) r
(4.) ~ q {OK.: 2}
(5.) p {z.d.n.}
(6.) r ∧ p {DK: 3, 5}
(7.) q {RO: 1, 6}
Sprz. {4, 7}
Przykład treściowy.
Jeżeli jest słonecznie i jest ciepło, to opalam się
Jeżeli jest słonecznie i nie opalam się, to nie jest ciepło.
Dowód wprost reguły transpozycji złożonej
(1.) (r ∧ p) → q {zał.}
(2.) r ∧ ~ q
(3.) r {OK.: 2}
(4.) ~ q
(5.) ((r ∧ p) → q) → ~ (r ∧ p) ∨ q {T}
(6.) ~ (r ∧ p) ∨ q) {RO: 1 i 5}
(7.) ~ p ∨ q {OA: 3 i 6}
(8.) ~ p {OA: 4 i 7}
Dowód wprost reguły transpozycji
p → q
~ q → ~ p
Dowód. (1.) p → q {zał.}
(2.) ~ q
(3.) (p → q) ∧ ~ q → ~ p {Toll.}
(4.) (p → q) ∧ (~ q) {DK: 1, 2}
~ p {RO: 3, 4}
Prawo zwrotności implikacji: p → p
Dowód: (1.) p {zał.}
(2.) ~ p {z.d.n.}
Sprz. {1, 2}
Reguła mnożenia implikacji:
p → q
r → s
(p ∧ r) → (q ∧ s)
Dowód: (1.) p → q
(2.) r → s {zał.}
(3.) p ∧ r
(4.) p {OK.: 3}
(5.) r
(6.) q {RO: 1, 4}
(7.) s {RO: 2, 5}
q ∧ s {DK: 6, 7}
Jeżeli jest zimno, to trzeba ubrać płaszcz.
Jeżeli pada deszcz, to trzeba zabrać parasol.
Jeżeli jest zimno i pada deszcz, to trzeba ubrać płaszcz i wziąć parasol.
Reguła dodawania implikacji stwierdza niezawodność schematu:
p → q
r → s
(p ∨ r) → (q ∨ s)
Dowód: (1.) p → q
(2.) r → s {zał.}
(3.) p ∨ r
(4.) ~ (q ∨ s) {z.d.n.}
(5.) ~ q ∧ ~ s {NA: 4}
(6.) ~ q {OK: 5}
(7.) ~ s
(8.) ~ p {Toll: 1, 6}
(9.) ~ r {Toll: 2, 7}
(10.) r {OA: 3, 9}
Sprz. {9, 10}
Reguła negowania alternatywy.
~ (p ∨ q)
~ p ∧ ~ q
Nieprawda, że (A jest bratem B lub A jest siostrą B)
A nie jest bratem B i A nie jest siostrą B
Dowód.
(1.) ~ (p ∨ q) {zał.}
(2.) p ∨ q {z.d.n.}
Sprz. {1, 2}
Reguła dylematu konstrukcyjnego złożonego.
p → q
r → s
p ∨ r
q ∨ s
Jeżeli polecę samolotem, będę na miejscu o 7 godz. rano.
Jeżeli pojadę pociągiem, to będę na miejscu o 10 godz. rano.
Polecę samolotem lub pojadę pociągiem.
Będę na miejscu o 7 godz. rano lub będę na miejscu o 10 godz. rano.
Dowód: (1.) p → q
(2.) r → s {zał.}
(3.) p ∨ r
(4.) (p → q) ∧ (r → s) {DK: 1, 2}
(5.) (p → q) ∧ (r → s) → (p ∨ r) → (q ∨ s) {Dod.impl.4}
(6.) (p ∨ r) → (q ∨ s) {RO: 5, 4}
q ∨ s {RO: 3, 6}
Prawo mnożenia następników.
[(p → q) ∧ (p → r)] ≡ [p → (q ∧ r)]
Bierzemy twierdzenia:
T1: p → (q ∧ r)] → (p → q)
T2: p → (q ∧ r)] → (p → r)
Dowód. (b): (1.) p → (q ∧ r) {zał.}
(2.) p → (q ∧ r) → (p → q) {T1}
(3.) p → (q ∧ r) → (p → r) {T2}
(4.) p → q {RO: 2, 1}
(5.) p → r { RO: 3, 1}
(p → q) ∧ (p → r) {DK.: 4, 5}
Uwaga. Aby unikać przeprowadzania osobnych dowodów twierdzeń pomocniczych wprowadzamy następujący zapis dowodu:
[p → (q ∧ r)] → (p → q) ∧ (p → r)
Dowód: (1.) p → (q ∧ r) {zał.}
(1.1) p {d.z.d.}*
(1.2) q ∧ r {RO: 1; 1.1}
(1.3) q {OK: 1, 2}
(1.4) r
(2.) p → q {1.1 - 1.3}
(3.) p → r {1.1 - 1.4}
(p → q) ∧ (p → r) {DK: 2, 3}
* - dodatkowe założenie dowodu - {d.z.d}.
Wiersz o podwójnym numerze (1.1) jest w tym dowodzie założeniem dodatkowym (d.z.d.). W dowodzie założeniowym można przyjąć dowolne wyrażenie jako założenie dodatkowe. Z założeń dowodu i założenia dodatkowego można wyprowadzić dowolne wiersze na podstawie opisanych wyżej reguł. Wiersze te mają również numery podwójne, dla zaznaczenia, że są one uzyskane na podstawie założenia dodatkowego. Wiersze o podwójnym numerze nie mogą kończyć dowodu, bo nie są uzyskane wyłącznie na podstawie założeń dowodu, lecz na podstawie założenia dodatkowego, którym może być postać dowolne wyrażenia.
Jeżeli jednak na podstawie założeń dowodu i założenia dodatkowego uzyskamy jakieś wyrażenie, to do dowodu można dołączyć - już jako wiersz o pojedynczym numerze - implikację, której poprzednikiem jest to założenie dodatkowe, a następnikiem wyrażenie uzyskane w dowodzie na jego podstawie.
Podany powyżej zapis części (b) dowodu, można uważać za skondensowany niejako zapis trzech dowodów osobnych. Wiersze (1.), (1.1 - 1.3) - stanowią dowód twierdzenia T1, wiersze (1.) i (1.1 - 1.4) stanowią dowód twierdzenia T2, zaś wiersze (1.), (2.) i (3.) uzupełnione o T1 i T2 po wierszu (1.), stanowią dowód właściwego twierdzenia.
Pragmatyczny wymiar rachunku zdań
Jeśli mamy koniunkcję pewnej liczby przesłanek, z których każda może być dowolnym wyrażeniem logicznym różnym od wyrażenia fałszywego i takich, że żadne dwie przesłanki nie są ze sobą sprzeczne, to możemy spytać o to, jakie wnioski mogą wynikać z tych przesłanek. Zastrzegamy niesprzeczność przesłanek, bo z fałszywych przesłanek może wynikać wszystko.
Generowanie wniosków z przesłanek.
Koniunkcję przesłanek doprowadzamy do postaci normalnej koniunkcyjno - alternatywnej, a następnie każdy człon koniunkcji lub tylko niektóre, uzupełniamy o brakujące w nich zmienne, które występują w koniunkcji przesłanek. Otrzymujemy nową postać normalną koniunkcyjno - alternatywną, lecz taką, że w każdym członie koniunkcji występują wszystkie zmienne, ale tylko w jednej postaci (z negacją lub bez negacji).
Uwaga. Jeżeli koniunkcja przesłanek będzie tautologią, to nie otrzymamy żądanej formy normalnej.
Przykład. Mamy dane przesłanki p → q, ~ (p ∨ q). Tworzymy ich koniunkcję
(p → q) ∧ ~ ( p ∨ q).
Koniunkcję przekształcamy w postać normalną k.a.
(~ p ∨ q) ∧ (~ p ∧ q) ≡ (~ p ∨ q) ∧ (~ p) ∧ (~ q).
Dwa ostanie człony koniunkcji nie zawierają żądanej formy. Każdy z tych członów uzupełniamy o takie wyrażenie, które nie zmieni jego wartości logicznej, a zarazem będzie zawierało brakujące zmienne.
Więc
(~ p ∨ q) ∧ [~ p ∨(q ∧ ~ q)] ∧ (~ q ∨ (p ∧ ~ p)] ≡
≡ (~ p ∨ q) ∧ (~ p ∨ q) ∧ (~ p ∨ ~ q) ∧ (~ q ∨ p) ∧ (~ q ∨ ~ p).
Porządkujemy człony i pozbywamy się członów powtarzających się.
(~ p ∨ q) ∧ (~ p ∨ q) ∧ (~ p ∨ ~ q) ∧ (p ∨ ~ q) ∧ (~ q ∨ ~ p) ≡
≡ (~ p ∨ q) ∧ (p ∨ ~ q) ∧ (~ p ∨ ~ q).
Człon (~ p ∨ q) i (~ p ∨ ~ q) powtarzał się.
Ostatecznie wyrażenie
a = (p → q) ∧ ~ ( p ∨ q)
jest równoważne formie normalnej
a' = (p ∨ ~ q) ∧ (~ p ∨ q) ∧ (~ p ∨ ~ q).
Jakie możemy otrzymać wnioski z naszych przesłanek zapisanych w formie normalnej.
Będą nimi:
(p ∨ ~ q) ≡ (q → p)
(~ p ∨ q) ≡ (p → q)
(~ p ∨ ~ q) ≡ (p → ~ q) ≡ (q → ~ p)
(p ∨ ~ q) ∧ (~ p ∨ q) ≡ (q → p) ∧ (p → q) ≡ (p ≡ q)
(p ∨ ~ q) ∧ (~ p ∨ ~ q) ≡ ~ q ∨ (p ∧ ~ p) ≡ ~ q
(~ p ∨ q) ∧ (~ p ∨ ~ q) ≡ ~ p ∨ (q ∧ ~ q) ≡ ~ p
(p ∨ ~ q) ∧ (~ p ∨ q) ∧ (~ p ∨ ~ q) ≡ (~ p ∧ ~ q).
Wnioski te wynikają z własności tautologii rachunku zdań, czyli z takich np. praw, jak:
p → p
(p ∧ q) → p
(p ∧ q) → q
(p ∧ q) → (p ∧ q), itd.
Jeżeli mamy n - członów koniunkcji, to otrzymuje się 2n - 1 wniosków. Przytoczona tu postać normalna ma tę własność, że jest ona jedyna dla danego wyrażenia a. Dlatego wnioski też są jednoznaczne.
Można teraz stosując dowolny sposób sprawdzania tautologiczności wyrażeń logicznych sprawdzić, czy otrzymane wnioski są poprawne. Weźmy np. wniosek 3. i jego przesłanki. Otrzymujemy wyrażenie:
[(p → q) ∧ ~ (p ∨ q)] → (p → ~ q)
Dowód (nie wprost): 1. p → q
2. ~ (p ∨ q) {zał.}
3. p
4. q {z.d.n.}
5. p ∨ q {DA: 3, 4}
Sprz. {2, 5}
Weźmy jeszcze przesłanki z wnioskiem 7.
{[(p → q) ∧ ~ (p ∨ q)] → (~ p ∧ ~ q)} ≡
≡ { ~ (~ p ∨ q) ∨ (p ∨ q) ∨ (~ p ∧ ~ q)} ≡
≡ [(p ∧ ~ q) ∨ (p ∨ q) ∨ (~ p ∧ ~ q)] ≡
≡ (p ∧ ~ q) ∨ [(p ∨ q) ∨ (~ p ∧ ~ q)] ≡
≡ (p ∧ ~ q) ∨ [(p ∨ q ∨ ~ p) ∧ (p ∨ q ∨ ~ q)] ≡
≡ [(p ∧ ~ q) ∨ (p ∨ q ∨ ~ p)] ∧ [(p ∧ ~ q) ∨ (p ∨ q ∨ ~ q)] ≡
≡ [(p ∨ ~ p ∨ q ∨ p) ∧ (p ∨ ~ p ∨ q ∨ ~ q) ∧
∧ (p ∨ ~p ∨ ~ q ∨ ~p) ∧ (p ∨ q ∨ ~ q ∨ ~q)] ≡
≡ (p ∨ q ∨ ~ q) ∧ (p ∨ ~ q ∨ q ∨ ~ q)
Widać, że jest to również tautologia.
Można problem odwrócić i zapytać o postać przesłanek, gdy dany jest wniosek w postaci wyrażenia F (p1, p2, …, pn). Postępowanie jest podobne do poprzedniego. Dążymy do otrzymania z normalnej postaci koniunkcyjno - alternatywnej formy wzbogaconej o brakujące zmienne w poszczególnych członach koniunkcji. Następnie osobno wypisujemy brakujące człony z kombinacjami zmiennych, czyli te, których jest brak w formie normalnej. Jako przesłanki będą kombinacje koniunkcji brakującego członu i wniosku, koniunkcji wniosku i dwóch brakujących członów, itd. W końcu bierzemy wniosek i wszystkie brakujące człony. Stanowią one przesłanki danego wniosku.
Przykład. Z jakich przesłanek pochodzi następujący wniosek: X ≡ Y?
(X ≡ Y) ≡ (X ∨ ![]()
) ∧ (![]()
∨ Y) - postać normalna
Brakujące człony to (X ∨ Y), (![]()
∨ ![]()
)
(![]()
- negacja X, ![]()
- negacja Y).
Szukanymi przesłankami będą wyrażenia:
(X ≡ Y) ∧ (X ∨ Y)
(X ≡ Y) ∧ (
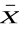
∨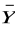
)(X ≡ Y) ∧ (X ∨ Y) ∧ (
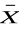
∨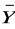
).
Wyrażenie te dają się przekształcić do form prostych:
(X ≡ Y) ∧ (X ∨ Y) ≡ (X ∨ Y) ∧ (
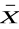
∨ Y) ∧ (X ∨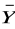
) ≡ (X ∧ Y)(X ≡ Y) ∧ (
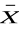
∨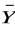
) ≡ (X ∨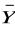
) ∧ (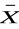
∨ Y) ∧ (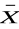
∨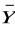
) ≡ (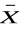
∧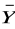
)(X ≡ Y) ∧ (X ∨ Y) ∧ (
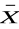
∨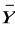
) ≡ (X ∨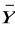
) ∧ (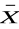
∨ Y) ∧ (X ∨ Y) ∧ (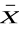
∨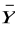
) ≡ 0.
3. jest przesłanką fałszywą, wynika z niej cokolwiek, a więc wyrażenie X ≡ Y.
Sprawdzimy jeszcze, czy np. przesłanka 1. i wniosek tworzą tautologię.
a = {(X ≡ Y) ∧ (X ∨ Y) → (X ≡ Y)}
Dowód (wprost):
X ≡ YX ∨ Y {zał.}
X → YY → X {OE: 1}
X ≡ Y {DE: 3, 4}
Sprawdzimy to wyrażenie w inny sposób.
a jest wyrażeniem typu:
a = [(p ∧ q) → p] ≡ [ ~ p ∨ ~ q ∨ p] - tautologia
Stosując podstawienie:
p / (X ≡ Y)
q / (X ∨ Y),
otrzymujemy a - czyli tautologię.
Przykład. Znaleźć wyrażenie F (X, Y) będące wnioskiem przesłanek:
X → Z
Y ≡
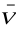
Z → V
Tworzymy tablicę prawdziwościową dla przesłanek.
X |
Z |
X →Z |
Y |
V |
Y ≡ |
|
Z |
V |
Z → V |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
oraz dla F (X, Y)
X |
Y |
V |
Z |
F(X, Y) |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
X |
Y |
Z |
V |
|
X → Z |
Z → V |
Y ≡ |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
Jak wypełniony jest pierwszy wiersz ostatniej tabelki? Żeby X → Z było prawdziwe, trzeba, by X = 1 i Z = 1 ostatniej tabeli aby przy Z = 1, Z → V było prawdziwe, trzeba, by V = 1, aby przy V ≡ 1, Y ≅ ![]()
było prawdziwe, potrzeba, by Y = 0. F (X, Y) ma cztery wiersze, więc trzy następne analizujemy podobnie.
Teraz wybieramy zmienne X i Y z ostatniej tablicy i otrzymujemy:
X |
Y |
F(X, Y) |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
Przy wierszu X = 1 i Y = 1, F(X, Y) = 0.
Więc ostatecznie
X |
Y |
F(X, Y) |
|
|
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
F(X, Y) = (X ∧ ![]()
) ∨ (![]()
∧ Y) ∨ (![]()
∧ ![]()
) ≡ (X ∧ ![]()
) ∨ [![]()
∧ (Y ∨ ![]()
)] ≡ (X ∧ ![]()
) ∨ ![]()
≡
≡ (X ∨ ![]()
) ∧ (![]()
∨ ![]()
) ≡ (![]()
∨ ![]()
).
Zasada rezolucji
Znamy kilka sposobów sprawdzania tautologiczności wyrażeń logicznych.
Są nimi:
metoda matrycowa (zero - jedynkowa).
metoda skrócona (jeśli dane wyrażenie a stanowi implikacja).
metoda aksjomatyczna.
metoda założeniowa.
Dwie ostatnie metody dla niektórych wyrażeń mogą okazać się zbyt trudne w wykazaniu ich tautologiczności. W roku 1965 J.A. Robinson opracował bardzo prostą regułę wnioskowania do automatycznego dowodzenia twierdzeń.
Załóżmy, że mamy dany pewnie zbiór S przesłanek o skończonej liczbie zmiennych. Wszystkie przesłanki łączymy w koniunkcję i całe wyrażenie doprowadzamy do postaci normalnej koniunkcyjno - alternatywnej. Bierzemy koniunkcję dwóch dowolnych członów postaci n.k.a., lecz takich by w jednym z nich występowała pewna zmienna bez negacji, a w drugim członie z negacją (lub odwrotnie). Wykreślamy z obu członów te zmienne i jako rezultat zapisujemy alternatywę pozostałych zmiennych z obu członów koniunkcji.
Przykład. Niech S = {p, p → q, p → r, ~ r}
Tworzymy koniunkcję przesłanek
a = p ∧ (p → q) ∧ (p → r) ∧ ~ r.
Teraz tworzymy postać n.k.a.
a` = p ∧ (~ p ∨ q) ∧ (~ p ∨ r) ∧ ~ r.
Bierzemy np. (~ p ∨ r) ∧ ~ r. Jako wynik zastosowania reguły wnioskowania zwanej zasadą rezolucji będzie tu wyrażenie ~ p. Zasadę rezolucji możemy ująć w postać schematu wnioskowania następująco:
(p ∨ q ∨ ~ r ∨ …∨ s) ∧ (~ p ∨ r ∨ … ∨ z)
(p ∨ q ∨ … s ∨ r ∨ … ∨ z)
Uwaga. W każdym członie koniunkcji może być więcej zmiennych z negacją niż jedna. Np. (p ∨ ~ q ∨ ~ r ) ∧ (~ p ∨ ~ s ∨ r). Jako wynik możemy otrzymać w tej sytuacji dwa osobne wyrażenia. Jedno ze względu na zmienną p i jej negację, drugie ze względu na zmienną r i jej negację, czyli jako wynik zastosowania zasady rezolucji do powyższych dwóch przesłanek mamy wyrażnia:
(~ q ∨ ~ r ∨ ∨ ~ s ∨ r)
oraz
(p ∨ ~ q ∨ ~ p ∨ ~ s).
Weźmy raz jeszcze dwa dowolne wyrażenia podpadające pod zasadę rezolucji.
Np.
(~ p ∨ q) ∧ ~ q
~ p
(~ p ∨ q) i ~ q nazywają się klauzulami a ~ p nazywa się rezolwentą.
Jak stosować zasadę rezolucji w dowodzeniu poprawności logicznej (tautologiczności) schematów wnioskowania bądź praw logiki. Wyjaśnimy to na konkretnym przykładzie.
Weźmy następujący schemat logiczny:
p → q
r → s
p ∨ r
q ∨ s
Stosując zasadę rezolucji pokazać, że jest to schemat wnioskowania.
Postępowanie:
wyrażenia nad kreską łączymy w koniunkcję
(p → q) ∧ (r → s) ∧ (p ∨ r).
wyrażenie to doprowadzamy do postaci normalnej koniunkcyjno - alternatywnej
(~ p ∨ q) ∧ (~ r ∨ s) ∧ (p ∨ r).
każdy człon koniunkcji stanowi osobną klauzulę.
wypisujemy je każdą w osobnym wierszu kolumny i jednocześnie numerujemy je:
~ p ∨ q
~ r ∨ s
p ∨ r.
5. negujemy wniosek (wyrażenie pod kreską) i zanegowany wniosek doprowadzamy do postaci n.k.a.,
~ (q ∨ s) ≡ (~ q) ∧ (~ s).
6.poszczególne człony koniunkcji dopisujemy do poprzedniej kolumny otrzymując zbiór klauzul.
1. ~ p ∨ q
2. ~ r ∨ s
3. p ∨r
4. ~ q
5. ~ s
7. Podkreślamy ten zbiór poziomą kreską.
1. ~ p ∨ q
2. ~ r ∨ s
3. p ∨r
4. ~ q
5. ~ s
do poszczególnych wybranych par klauzul stosujemy zasadę rezolucji, otrzymane rezolwenty numerujemy kolejnymi liczbami, zaznaczając z boku resolwenty numery klauzul, z których została otrzymana resolwenta. Rezolwenty traktujemy jako nowe klauzule, do których wolno stosować jest zasadę rezolucji. Postępowanie to kontynuujemy tak długo, aż otrzymamy dwa wiersze sprzeczne. Z nich otrzymuje się rezolwentę (klauzulę) pustą. Klauzula pusta kończy dowód ( - klauzula pusta - oznaczenie).
stosowanie zasady rezolucji stanowi dowód nie wprost. Więc, jeśli jakiś schemat jest tautologią, to zaprzeczony wniosek musi doprowadzić do sprzeczności.
Dowód naszego przykładu jest więc następujący.
~ p ∨ q
~ r ∨ s
p ∨ r
~ q
~ s
~ p (1. i 4.)
~ r (2. i 5.)
p (3. i 7.)
(6. i 8.)
Kilka innych typowych przypadków wnioskowania z użyciem zasady rezolucji przedstawia poniższa tabela.
Tabela. Zasada rezolucji, przesłanki i rezolwenty.
Przesłanki |
Resolwenty |
Uwagi
|
p ~ p ∨ q, (p → q) |
q |
modus poneus |
p ∨ q ~ p ∨ q |
q |
q ∨ q daje q Rezolwenta sklejana |
p ∨ q ~ p ∨ ~ q |
p ∨ ~ p q ∨ ~ q |
dwie rezolwenty, obie tautologie |
p ~ p |
|
klauzula pusta Oznaka sprzeczności |
~ p ∨ q, (p → q) ~ q ∨ r, (q → r) |
~ p ∨ r (p → r) |
wnioskowanie „łańcuchowe” |
Powyższa tabela wskazuje, że za pomocą zasady rezolucji można (automatycznie) otrzymywać bezpośrednie wnioski z danych przesłanek.
Przykład. Stosując zasadę rezolucji zbadać jaki lub jakie wnioski wynikają z danego zbioru przesłanek.
Przesłanki: S = {p → q, p → r, ~ q ∨ ~ r}.
Tworzymy klauzule:
~ p ∨ q
~ p ∨ r
~ q ∨ ~ r
~ p ∨ ~ r (1. i 3.)
~ p (2. i 4.)
~ p ∨ ~ q (3. i 4.)
4., 5. i 6. stanowią bezpośrednie wnioski trzech powyższych przesłanek.
Zasada rezolucji może też stanowić ważne narzędzie badawcze w sprawdzaniu niesprzeczności danego zbioru przesłanek. Jeżeli zbiór przesłanek jest sprzeczny, tzn. jego koniunkcja ma wartość logiczną zero, to nie może być użyty do wnioskowania.
Przykład. Zbadać niesprzeczność następującego zbioru przesłanek:
S = {p ∨ q, p → r, ~ q ∨ r, ~ r}
Tworzymy klauzule
p ∨ q
~ p ∨ r
~ q ∨ r
~ r
~ p (2. i 4.)
~ q (3. i 4.)
p (1. i 6.)
(5. i 7.)
Zbiór S przesłanek jest sprzeczny.
Na koniec rozwiążemy zasadą rezolucji problem znalezienia wniosku F(X, Y) wiążącego zmienne X i Y, który wynika ze zbioru następujących przesłanek:
X → Z
Y ≡ ~ V
Z → V.
Tworzymy z tych przesłanek klauzule i szukamy takiej rezolwenty, która składa się tylko ze zmiennych X i Y.
~ X ∨ Z
~ Y ∨ ~ V
V ∨ Y
~ Z ∨ V
~ X ∨ V (1. i 4.)~ X ∨ ~ Y (2. i 5.)
6. jest pożądanym wnioskiem.
Więc F (X, Y) ≡ ~ X ∨ ~ Y. Poprzednia analiza logiczna dała ten sam wynik, lecz droga analizy była dłuższa.
Zadania.
Znaleźć wszystkie wnioski z przesłanek.
p → q i p
p ≡ q i ~ p
p ∨ q i p i ~ q
p → q i q → r.
Znaleźć wszystkie wnioski dla następującego zbioru przesłanek:
A1. Jeśli suma cyfr pewnej liczby całkowitej x jest podzielna przez 3, to liczba x jest podzielna przez 3 lub przez 9.
A2. Jeśli liczba jest podzielna przez 9, to jest też podzielna przez 3.
B1. Jeśli w danym czworokącie dwa leżące naprzeciw siebie boki są równoległe i równe, to ten czworokąt jest równoległobokiem.
B2. W danym czworoboku dwa leżące naprzeciw siebie boki są równe lub są równoległe.
Znaleźć wszystkie przesłanki, których wnioskiem jest:
A). p → q
B). p ∨ ~ q
C). ~ (p ∨ q)
D).(p ∨ q) → (p ∧ q).
Ustalić jaki związek logiczny zachodzi między zdaniem: „dany czworokąt jest rombem”, „dany czworokąt jest kwadratem” na podstawie przesłanek”
jeżeli dany czworokąt jest rombem, to jego przekątne są prostopadłe.
jeżeli przekątne danego czworokąta nie są prostopadłe, to czworokąt ten nie jest kwadratem.
jeżeli dany czworokąt jest kwadratem, to można go wpisać w okrąg.
nieprawdą jest, że w danym czworokącie przekątne są prostopadłe do siebie lub może być wpisany w okrąg.
Znaleźć wszystkie przesłanki zawierające zmienne p i q dla wniosku
p
~ p
Stosując zasadę rezolucji, znaleźć wyrażenie wiążące zmienne p i q jako wniosek dla przesłanek:
~ p ∨ r, ~ r ∧ ~ q, q → p.
~ p ∨ r, q → ~ r, s → q ∧ r, s ∨ p.
Rachunek kwantyfikatorów
Pojęcie kwantyfikatora i predykatu
Początki rachunku zdań sięgają starożytności. Pojęcie kwantyfikatora natomiast powstało dopiero w drugiej połowie XIX wieku, a rachunek kwantyfikatorów w obecnej postaci sformułowany został dopiero w początkach XX wieku. Aby pojęcie to wprowadzić systematycznie, należy zastanowić się nad językiem teorii, w których spotykamy kwantyfikatory. Teorie te mówią o różnych dziedzinach, szczególnie matematyki. Zmienne tych teorii reprezentują dowolne obiekty - indywidua danej dziedziny. Są one jakby nazwami przedmiotów, o których w danej teorii jest mowa, np. liczb, punktów, zbiorów, ludzi, zwierząt, itd. O przedmiotach tych mówi się za pomocą pewnych wyróżnionych zwrotów. Zwroty te opisują pewne relacje między obiektami lub pewne własności tych przedmiotów. Mówiąc np. o liczbach używamy na porządku dziennym takich zwrotów, jak: x = y, x = y + z, x = y ∗ z, x > y. Za pomocą tych zwrotów oraz spójników zdaniowych i kwantyfikatorów, o których niebawem będzie mowa, określić można wiele inny zwrotów. Tego rodzaju wyrażenia zawierające zmienne zwie się funkcjami zdaniowymi lub predykatami. Predykat lub funkcja zdaniowa jest to więc wyrażenie zawierające pewne zmienne i opisujące pewne własności lub pewną relację.
Predykat x > 0 opisuje własność bycia liczbą dodatnią. Predykat x = y opisuje relację identyczności, funkcja zdaniowa x = 2y (x + z) opisuje pewną własność między trzema liczbami, określoną za pomocą dodawania i mnożenia. Wśród predykatów dowolnej teorii (matematycznej) można zawsze wyróżnić predykaty atomiczne, nie zawierające w sobie żadnej części, która byłaby predykatem (zwroty pierwotne, wyjściowe), oraz predykaty złożone, stanowiące mniej lub bardziej skomplikowane zestawienia zwrotów pierwotnych. W arytmetyce np. predykat x = y + z jest traktowany jako pierwotny, natomiast zwrot „x jest liczbą pierwszą” nie jest zwykle uważany za zwrot wyjściowy, bo daje się wypowiedzieć za pomocą dodawania i mnożenia.
W dalszych rozważaniach nie będziemy interesowali się predykatami żadnej konkretnej dziedziny. Założymy ogólnie, że każda dziedzina (wiedzy) zawiera pewną ilość predykatów opisujących pewne własności i relacje między obiektami rozważanej dziedziny. Konkretny sens owych relacji będzie nam przez czas pewien obojętny. Dlatego na oznaczenie predykatów będziemy używali zwrotów nie mających ustalonego znaczenia, jak np. następujące formuły:
P(x), R(x, y), S(x, y, z), T(x, y, z, v), itd.
Wyrażenia te będą nam zastępowały wszelkie dowolne predykaty o takiej liczbie zmiennych, jaka występuje w nawiasie po danej literze. A więc P(x) oznaczać może zarówno x > 0, jak i własność „x jest parzyste”, „x jest duże, R(x, y) oznaczać może zarówno x > y, jak i x = y, czy też „x jest ojcem y”.
Przypuśćmy na chwilę, że interesują nas tylko liczby naturalne. Liczby te mają swoje nazwy. Nazwami tymi są cyfry: 0, 1, 2, 3, 4, … Jeżeli pewna własność opisaną za pomocą predykatu P(X) ma liczba 1, to fakt ten zapisujemy za pomocą wyrażenia P(1). Zdania: P(1), P(2), P(3), P(4) mówią więc, że własność opisana przez predykat P(X) mają liczby 1, 2, 3, 4. Może to być np. własność x > 0. Wówczas wymienione zdania są prawdziwe i mają postać 1 > 0, 2 > 0, 3 > 0, 4 > 0. Jeśli chcemy powiedzieć w jednym zdaniu, że wszystkie cztery liczby 1, 2, 3, 4 mają własność P, wówczas cztery wymienione powyżej zdania łączymy w koniunkcję
P(1) ∧ P(2) ∧ P(3) ∧ P(4).
Gdybyśmy chcieli w podobny sposób powiedzieć, że każda liczba naturalna ma własność P, musielibyśmy napisać koniunkcję nieskończoną
P(0) ∧ P(1) ∧ P(2) ∧ P(3) ∧ …
Ponieważ napisanie koniunkcji nieskończonej jest niewykonalne, przeto musimy się zadowolić jakimś wyrażeniem skończonym. Najprościej jest wtedy posłużyć się zwrotem
Dla każdego x, P(X)
Zwrot „dla każdego x …” zwie się kwantyfikatorem ogólnym wiążącym zmienną x i skracany bywa w symbolu
∀ x …
Zdanie (x) symbolicznie zapisujemy więc następująco:
(3) ∀ x P(x).
Czytamy: „ dla każdego x, P od x „.
Nieskończone zdanie (1) można uważać za równoważne zdaniu (3) w przypadku, gdy jedynymi rozważanymi przez nas przedmiotami są liczby naturalne.
(4) ∀ x P(x) ≡ P(0) ∧ P(1) ∧ P(2) ∧ P(3) ∧ …
Równoważność (4) można uważać za nieformalną definicję kwantyfikatora ogólnego. Kwantyfikator ogólny jest to więc jak gdyby nieskończona koniunkcja.
Podobne rozważania prowadzą do wniosku, że kwantyfikator szczegółowy, czyli zwrot „przy pewnym x, …” jest jak gdyby nieskończoną alternatywą. Jeśli chcemy powiedzieć, że istnieje taka liczba wśród liczb mniejszych od 5, która ma własność P, możemy myśl tę wyrazić za pomocą alternatywy
P(0) ∨ P(1) ∨ P(2) ∨ P(3) ∨ P(4).
Ową liczbą mniejszą od 5 może być bowiem tylko jedna z liczb 0, 1, 2, 3, 4. Chcąc w podobny sposób powiedzieć, że istnieje w ogóle jakaś liczba naturalna mająca własność P, trzeba by użyć alternatywy nieskończonej
(5) P(0) ∨ P(1) ∨ P(2) ∨ P(3) ∨ P(4) ∨ P(5) ∨ …
Zwrot „istnieje takie x, że …” uważamy za równoważny zwrotowi „dla pewnego x, …” Symbolicznie zwroty te zapisujemy za pomocą jednego wyrażenia ∃x… zwanego kwantyfikatorem szczegółowym lub egzystencjalnym. Jeśli rozpatrywanymi przez nas przedmiotami są tylko liczby naturalne, wówczas alternatywę nieskończoną (5) można uważać za równoważną wyrażeniu ∃ x P(x):
(6) ∃ x P(x) ≡ P(0) ∨ P(1) ∨ P(2) ∨ …
Równoważność tę można uważać za nieformalną definicję kwantyfikatora egzystencjalnego stosowanego do liczb naturalnych.
Zwroty nazwane powyżej kwantyfikatorami grają ważną rolę w budowie wszelkiego rodzaju teorii - dziedzin wiedzy. Dział logiki, który tym się zajmuje nazywa się rachunkiem kwantyfikatorów i podaje on sposoby poprawnego posługiwania się kwantyfikatorami. Zanim opiszemy rachunek kwantyfikatorów, należy jeszcze zająć się bliżej pojęciem predykatu, jako zwrotu określającego pewną własność lub pewną relację. Pewne własności predykatów są bowiem niezbędne do opisu rachunku kwantyfikatorów.
Kwantyfikatory są najważniejszym narzędziem budowy nowych predykatów.
Zilustrujemy to na przykładzie. Predykat x ≤ z opisuje pewną relację (dwuargumentową). Natomiast wyrażenie
(7) ∀ z (x ≤ z)
nie określa już żadnej relacji, lecz definiuje pewną własność liczby x, taką mianowicie, że każda liczba z jest od liczby x większa lub jej równa. Inaczej: x jest najmniejszą z rozważanych liczb. Jeśli odnosiłoby się to tylko do liczb naturalnych, byłaby to liczba zero. Zauważmy, że w wyrażeniu (7) definiującym własność bycia najmniejszą liczbą, występują dwie litery (zmienne indywiduowe), to jednak rola ich nie jest jednakowa. Zmienną naprawdę, czyli jak to się mówi: zmienną wolną, jest tylko zmienna x, natomiast litera z w wyrażeniu (7) nie jest zmienną wolną. Litera z służy jedynie do opisu tej własności liczby x, o której w (7) jest mowa. Litera z jest związana kwantyfikatorem ∀z… . Odróżnienie zmiennych wolnych od zmiennych związanych odgrywa w rachunku kwantyfikatorów ważną rolę.
Rozważmy jeszcze jeden przykład, wyrażenie
(8) x + y = z
zawiera trzy zmienne wolne i opisuje przeto relację trójczłonową. Jeśli w (8) zwiążemy zmienną y kwantyfikatorem szczegółowym, to otrzymamy, jak już wiemy, predykat (wyrażenie dwuargumentowe) postaci
(9) ∃ y (x + y = z),
w odniesieniu do liczb naturalnych tym predykatem jest również x ≤ z. Jeśli do (9) dodany kwantyfikator ogólny wiążący zmienną z, to wyrażenie
(10) ∀ z ∃ y (x + y = z),
opisuje jedynie pewną własność pojedynczej liczby naturalnej x. Jest to ta sama własność bycia najmniejszą liczbą naturalną, którą opisywało również wyrażenie (7). Stosując do (10) kwantyfikator szczegółowy ∃ x …, wiążący ową jedyną zmienną wolną, otrzymujemy wyrażenie
(11) ∃ x ∀ x ∃ y (x + y = z),
które nie ma już zmiennych wolnych. Nie jest już ono żadnym predykatem, lecz jedynie zdaniem matematycznym.
Jeśli przedmiotami rozważanymi przez nas byłyby tylko liczby naturalne, wówczas zdanie (11) wyrażałoby tę samą myśl, co zdanie
∃ x ∀ z (x ≤ z).
Myśl tę można wypowiedzieć w zdaniu:
istnieje najmniejsza liczba naturalna.
Analiza tego typu wyrażeń prowadzi do wniosku, że określają one pewną relację między tyloma zmiennymi, ile zawiera w sobie zmiennych wolnych. Są nimi tylko te zmienne, które nie są związane żadnym kwantyfikatorem. Wyrażenia nie zawierające zmiennych wolnych nie są predykatami, nie określają żadnych relacji, ani własności, tylko są zdaniami prawdziwymi lub fałszywymi.
To, co do tej pory powiedzieliśmy o zmiennych, predykatach i zdaniach pozwala odpowiedzieć na pytanie, czy wyrażenie X jakiejś nawet bliżej nie określonej dziedziny jest predykatem (określa własność lub relację), czy też jest zdaniem (wyraża zamkniętą myśl) bez analizy sensu wyrażenia X, przyglądając się jedynie jego graficznej budowie. Określenia zmiennej wolnej i związanej mają czysto strukturalny charakter. Ogólnie jakieś pojęcie - wyrażenie dotyczące pewnej dziedziny - nazywamy składniowym (syntaktycznym), jeśli w określeniu tego pojęcia mowa jest tylko o kształcie napisu - budowy, a nie o jego, czy też ich, znaczeniu i z kształtu budowy (składni strukturalnej) rozstrzygamy, czym dane wyrażenie jest, predykatem czy zdaniem. Jeśli zaś w określeniu pojęcia dotyczącego pewnych wyrażeń nie można się obyć bez mówienia o znaczeniu (semantyce) tych wyrażeń, wówczas pojęcie to nazywamy semantycznym.
Pojęcia zmiennej wolnej i związanej, zdania i predykatu w zastosowaniu do analizy kształtu wyrażenia X mają charakter syntaktyczny. Jeśli natomiast operujemy w wyrażeniu X konkretnymi predykatami odnoszącymi się do konkretnej dziedziny, wówczas predykaty, bądź zdania interpretujemy semantycznie.
Aby lepiej zrozumieć syntaktyczny charakter wymienionych wyżej pojęć, należy dodatkowo przyjąć pewne relacje odnoszące się do kształtu napisów wyrażeń predykatowych lub zdań.
Relacjami tymi są:
napis X jest równokształtny z napisem Y,
napis X zawiera się w napisie Y (X jest częścią Y),
napis X następuje bezpośrednio po napisie Y (X bezpośrednio poprzedza Y).
Sens wymienionych relacji jest empirycznie łatwo uchwytny. Przykładowo: napis X jest równokształtny z napisem Y wtedy, gdy X i Y są dwoma egzemplarzami tego samego napisu, lecz znajdują się w różnych miejscach wyrażenia predykatowego lub zdania.
Definicja 1.A. Jeśli w zasięgu kwantyfikatora wiążącego pewną zmienną nie znajduje się żaden inny kwantyfikator, to zmiennymi związanymi tym kwantyfikatorem są wszystkie zmienne równokształtne ze zmienną objętą tym kwantyfikatorem i zawarte w jego zasięgu.
B. Jeśli w zasięgu kwantyfikatora początkowego wyrażenia A znajduje się jakiś kwantyfikator, to zmiennymi związanymi kwantyfikatorem początkowym wyrażenia A są wszystkie zmienne równokształtne ze zmienną objętą tym kwantyfikatorem i zawarte w jego zasięgu, które nie są związane żadnym kwantyfikatorem zawartym w zasięgu tego kwantyfikatora początkowego w wyrażeniu A.
C. Zmiennymi związanymi wyrażenia A nazywamy wszystkie zmienne zawarte w wyrażeniu A i związane kwantyfikatorami zawartymi w wyrażeniu A.
Po wprowadzeniu powyższych relacji możemy teraz przyjąć następujące definicje syntaktyczne.
Definicja 2.A. Kwantyfikatorem ogólnym nazywamy każdy znak należący do zbioru „∀”.
B. Kwantyfikatorem szczegółowym lub egzystencjalnym nazywamy każdy znak należący do zbioru „∃”.
C. Zmienną objętą kwantyfikatorem (będącą pod kwantyfikatorem) nazywamy dowolną literę występującą bezpośrednio po kwantyfikatorze.
D. O kwantyfikatorze tym mówimy wtedy, że wiąże tę zmienną.
Definicja 3. Zasięgiem kwantyfikatora wiążącym pewną zmienną nazywamy całe wyrażenie zawarte w nawiasie zaczynającym się bezpośrednio po zmiennej objętej owym kwantyfikatorem.
Zasięg kwantyfikatora początkowego wyrażenia A
∀ x (… x … x …)
zmienne związane kwantyfikatorem początkowym wyrażenia A
zmienna objęta kwantyfikatorem początkowym wyrażenia A (zmienna pod kwantyfikatorem)
kwantyfikator początkowy wyrażenia A
Rys.1. Schemat wyrażenia A zaczynającego się od kwantyfikatora i nie zawierającego kwantyfikatorów w swoim zasięgu.
Definicja 4. Pewna litera jest zmienną wolną wyrażenia A, gdy nie jest zmienną związaną wyrażenia A.
Z dwóch liter równokształtnych między sobą, zawartych w tym samym wyrażeniu A, jedna może być wolna, a druga związana, np. w wyrażeniu
(12) ∀ x (x = x) ∨ x = 0
znak czwarty i szósty są zmiennymi związanymi w (12), natomiast znak dziewiąty jest zmienną wolną w (12), nie jest bowiem zawarty w zasięgu żadnego kwantyfikatora. Z powyższych określeń wynika następujący pożyteczny sposób oznaczania, które zmienne są wolne, a które związane.
Pewna zmienna jest związana kwantyfikatorem Y wtedy, gdy zmienna ta jest wolna w wyrażeniu stanowiącym zasięg kwantyfikatora Y, a związana jest w wyrażeniu złożonym z kwantyfikatora Y, zmiennej nim objętej i z jego zasięgu.
Przykład.
(13) ∀ x (∀ x (x = x) ∨ x = 0).
W wyrażeniu (13) zmienna stanowiąca znak dwunasty jest związana pierwszym kwantyfikatorem wyrażenia (13), jest bowiem wolna w wyrażeniu stanowiącym zasięg tego kwantyfikatora. Natomiast znak siódmy i dziewiąty w wyrażeniu (13) są związane przez drugi kwantyfikator wyrażenia (13). Znak dwunasty i siódmy chociaż są równokształtne, to jednak są związane przez inne kwantyfikatory. Grają one rolę zmiennych zupełnie innego kształtu. W takich przypadkach trzeba zmienić kształt jednej z tych zmiennych, nie zmieniając kształtu drugiej, np. w zdanie
(14) ∀ z (∀ x (x = x) ∨ z = 0).
Postępowanie takie nazywa się w rachunku predykatów różnicowaniem zmiennych. Zatem dołączając do predykatów kwantyfikatory należy to czynić poprawnie, aby nie doprowadzić do wymienionej wyżej sytuacji związanej z kolizją zmiennych w otrzymanym nowym predykacie. Tworząc nowe wyrażenia predykatowe należy brać pod uwagę następujące dwa:
Wyrażenie predykatowe nie może zawierać dwóch zmiennych równokształtnych, z których jedna jest związana, a druga wolna.
Jedna i ta sama zmienna (lub dwie równokształtne) nie może być objęta jednocześnie dwoma różnymi kwantyfikatorami, jeśli nie jest zmienną wolną, czyli nie może być związana dwoma różnymi kwantyfikatorami.
Pozostaje jeszcze zdefiniować syntaktycznie pojęcie predykatu oraz zdania, gdyż z dotychczas przytaczanych przykładów, używane tam predykaty i zdania były symbolizowane semantycznie (wyrażały jakąś konkretną relację lub własność, x < y, x > 0, itd.) lub zdanie.
Definicja 5. Wyrażenie X jest predykatem n - argumentowym (n zmiennych), gdy jest poprawnie zbudowane i zawiera n zmiennych wolnych, z których żadne dwie nie są równokształtne, a każda inna zmienna wolna wyrażenia X jest równokształtna z którąś z owych n różnokształtnych między sobą.
Definicja 6. Wyrażenie X jest zdaniem (zdaniem zamkniętym) wtedy, gdy wyrażenie X jest poprawnie zbudowane i nie ma zmiennych wolnych.
Uściśliwszy pojęcie predykatu i zdania, powróćmy do sposobów rozumienia operacji związanych z kwantyfikatorami. Kwantyfikatory stosowane do liczb rzeczywistych mają bardzo przejrzystą interpretację geometryczną, jako operacje rzutowania i środkowania. Niech w dziedzinie liczb rzeczywistych ma miejsce relacja R (x, y) czyli predykat dwuargumentowy określony dla pewnych par <x, y〉 liczb rzeczywistych. Relację, jako zbiór łatwo jest odwzorować na płaszczyźnie w układzie kartezjańskim. Ponieważ każdemu w tym układzie punktowi płaszczyzny odpowiada w sposób wzajemnie jednoznaczny pewna para <x, y〉 liczb rzeczywistych, przeto relacje R określonej przez predykat R(x, y) liczb rzeczywistych odpowiada zbiór tych punktów z płaszczyzny, których współrzędne <xz, yz〉 pozostają do siebie w relacji R, czyli spełniają wzór: R(xz, yz). Zbiór ten oznaczymy przez R i będziemy go nazywali wykresem predykatu R (x, y). Rozpatrzmy teraz, jaką interpretację będzie miał predykat jednoargumentowy:
(15) ∃ y (R(x, y))
powstały przez dodanie kwantyfikatora szczegółowego do predykatu R(x, y). Ponieważ predykat (15) jest jednoargumentowy, przeto wykresem jego nie jest zbiór par, ale pewien zbiór liczb rzeczywistych x takich, dla których istnieją takie liczby y, że punkt <x, y〉 należy do zbioru R. Takim zbiorem jednoargumentowym jest po prostu rzut prostopadły zbioru R na oś x-ów (patrz rys.2.)
Rys.2. Rzut relacji R na oś x-ów.
Weźmy teraz predykat postaci
(16) ∀ y R (x, y)
Interpretację predykatu (16) stanowi zbiór położony na osi x - ów i złożony z takich liczb, że dla każdego y punkt <x, y〉 należy do zbioru R. Jest to więc zbiór tych x-ów, dla których cała prosta pionowa przechodząca przez x leży wewnątrz wykresu predykatu R(x, y) (zbiór S na rys.3.).
Rys.3. Środkowanie zbioru R na oś x-ów.
Zbiór S będziemy nazywali wynikiem operacji środkowania zbioru R. Powstaje on bowiem, jako rzut tych wszystkich promieni pionowych, które przechodzą przez zbiór R nie zostając zatrzymane przez punkty należące do uzupełnienia zbioru R.
Między operacjami rzutowania i środkowania zachodzi pewien ważny związek. Z rysunku 3 łatwo spostrzec, że uzupełnienie zbioru S do całej osi x-ów jest identyczne z rzutem na oś x-ów uzupełnienia zbioru R. Zatem predykaty
~ ∀ y R(x, y) i ∃ y ~ R(x, y)
mają taki sam wykres.
Otrzymujemy tu pierwsze w naszych rozważaniach twierdzenie logiki predykatów, a mianowicie zdanie
(18) ∀ x [∃ y ~ R(x, y) ≡ ~ ∀ y R(x, y)].
Wyrażenie poprzedzono kwantyfikatorem wiążącym zmienną x. Gdy x nie odgrywa żadnej roli, to (18) można zredukować do postaci
(19) ~ ∀ y R(x, y) ≡ ∃ y ~ R(x, y).
Zdanie (19) nazywa się prawem de Morgana dla rachunku kwantyfikatorów.
Na przykład dla R(x, y) = „x > y” zdanie to mówi:
Nie istnieją liczby mniejsze od x ≡ wszystkie liczby są nie mniejsze od x.
Temu zdaniu odpowiada postać prawa de Morgana:
~ ∃ R(x, y) ≡ ∀ ~ R(x, y).
Wiemy, jak interpretować wyrażenia rachunku predykatów. Teraz należy zapytać, jak należy budować i z „czego” należy budować te wyrażenia. Mamy następujące elementy (obiekty do budowy:
kwantyfikatory (∀, ∃)
predykaty (P(x), R(x , y ), …)
zmienne nazwowe (x, y, z, …)
stałe indywiduowe (a, b, c, …)
funktory klasycznego rachunku zdań ( ~, ∧, ∨, →, ≡ )
zmienne zdaniowe (p, q, r, …)
nawiasy ((), [], {}).
Z tych obiektów wszystkich razem sensownie ujętych lub tylko niektórych, tworzy się wyrażenia rachunku predykatów. Tak zbudowany rachunek nazywany jest logiką klasyczną, czyli zawiera on w sobie k.r.z. i dodatkowo wyrażenia, gdzie występują kwantyfikatory, predykaty i nawiasy. Dla rachunku kwantyfikatorów nie istnieje efektywna (algorytmiczna, np. zero - jedynkowa) metoda rozstrzygania prawdziwości wyrażeń tego rachunku, ale istnieje w odniesieniu do wyrażeń zbudowanych z kwantyfikatorów, zmiennych zdaniowych i predykatów jednoargumentowych (patrz np. J. Słupecki, K. Hałkowska, K. Piróg - Rzepecka, Logika i teoria mnogości, PWN, Warszawa 1994, str. 64-67).
W rachunku predykatów (kwantyfikatorów) podobnie jak w rachunku zdań wyrażenia (formuły) dzielą się na:
1. tautologie - twierdzenia
2. wyrażenia fałszywe (antytautologie)
3. wyrażenia spełnialne.
Jeżeli ograniczymy się tylko do predykatów jednoargumentowych, to można je podzielić na klasy: P, F i T.
Klasa P. Są to predykaty spełnione przez wszystkie wartości zmiennej w nich występującej.
Klasa F. Zawiera predykaty, które nie są spełnione przez żadną wartość zmiennej w nich występującej.
Klasa T. Są to wyrażenia spełnione przez niektóre lecz nie wszystkie wartości zmiennej w nich występującej.
Litery P, F i T są skrótami wyrażeń Prawda, Fałsz i Formy zdaniowe spełnione.
Zestawienie wszystkich związków pomiędzy należeniem predykatu jednoargumentowego do klas P, F lub T, a należeniem do tych klas całego wyrażenia zbudowanego za pomocą funktorów i zmiennych zdaniowych klasycznego rachunku zdań podają poniższe tabele.
Tabela 1.
P(x) |
Q(x) |
P(x)∧Q(x) |
P(x)∨Q(x) |
P(x)→Q(x) |
P(x)≡Q(x) |
P |
P |
P |
P |
P |
P |
P |
F |
F |
P |
F |
F |
P |
T |
T |
P |
T |
T |
F |
P |
F |
P |
P |
F |
F |
F |
F |
F |
P |
P |
F |
T |
F |
T |
P |
T |
T |
P |
T |
P |
P |
T |
T |
F |
F |
T |
T |
T |
T |
T |
F, T |
T, P |
T, P |
P, T, F |
Tabela 2.
P(x) |
~ P(x) |
P |
F |
F |
P |
T |
T |
Wyrażeniami jednoargumentowego rachunku predykatów są też następujące wyrażenia:
p ∧ Q (x), p ∨ Q (x), p → Q (x), Q (x) → p, …
(… oznacza: oraz wiele innych, np. ~ (p ∨ Q (x)).
Dla podanych powyżej wyrażeń przynależność ich do danej klasy wyraża tabela 3.
Tabela 3.
p |
Q (x) |
p∧Q(x0 |
p∨Q(x) |
p→Q(x) |
Q(x)→p |
1 |
P |
P |
P |
P |
P |
1 |
F |
F |
P |
F |
P |
1 |
T |
T |
P |
T |
P |
0 |
P |
F |
P |
P |
F |
0 |
F |
F |
F |
P |
P |
0 |
T |
F |
T |
P |
T |
Wyjaśnimy przykładowo, dlaczego warunek podany w ostatnim wierszu i czwartej kolumnie, należy do klasy T (patrz niżej tabela 4)
Tabela 4.
p |
Q(x) |
p∨Q(x) |
0 |
T |
T |
Wyrażenie (p ∨ Q(x)) należy do klasy T, bo predykat należy do klasy T, skoro predykat należy do klasy T, to istnieje taki obiekt (x = a) i (x = b), że jedno ze zdań Q (a) lub Q (b) jest prawdziwe, drugie - fałszywe. Stąd z uwagi, że p = 0, również jedna z alternatyw p ∨ Q (a), p ∨ Q (b) jest prawdziwa, druga fałszywa.
Podamy jeszcze tabelę wskazującą na zależność pomiędzy wartościami logicznymi zdań
∀ x P(x) i ∃ x P (x),
a klasą do której należy predykat P (x).
Tabela 5.
P(x) |
∀ x P(x) |
∃ x P(x) |
P |
1 |
1 |
F |
0 |
0 |
T |
0 |
1 |
Przykłady. Sprawdzimy za pomocą tablicy zdanie
∀ x P(x) → ∃ x P(x)
Tabela 6.
P(x) |
∀ x P(x) |
∃ x P(x) |
∀ x P(x)→∃ x P(x) |
P |
1 |
1 |
1 |
F |
0 |
0 |
1 |
T |
0 |
1 |
1 |
Jest to prawo jednoargumentowego rachunku kwantyfikatorów, wyrażone w postaci zdania.
Φ = ∃ x [P(x) ∨ Q(x)] → (∃ x P(x) ∨ ∃ x Q(x))
P(x)
|
Q(x) |
P(x)∨Q(x) |
∃ x P(x) |
∃ x Q(x) |
∃ x [P(x) ∨ Q(x)] |
∃ x P(x)∨∃Q(x) |
Φ |
P |
P |
P |
1 |
1 |
1 |
1 |
1 |
F |
P |
P |
0 |
1 |
1 |
1 |
1 |
T |
P |
P |
1 |
1 |
1 |
1 |
1 |
P |
F |
P |
1 |
0 |
1 |
1 |
1 |
F |
F |
F |
0 |
0 |
0 |
0 |
1 |
T |
F |
T |
1 |
0 |
1 |
1 |
1 |
P |
T |
P |
1 |
1 |
1 |
1 |
1 |
F |
T |
T |
0 |
1 |
1 |
1 |
1 |
T |
T |
T, P |
1 |
1 |
1 |
1 |
1 |
Widać, że 2. też jest prawem wyrażonym zdaniem.
Klasyfikacja zdań
(sylogistyka Arystotelesa a predykaty)
Jeśli mamy dane wyrażenie rachunku predykatów (jednoargumentowych) bez zmiennych wolnych, to jest ono zdaniem - konkretną myślą. Takich zdań możemy utworzyć teoretycznie nieskończenie wiele. Dla pragmatyki ważna jest klasyfikacja, czyli rozporządzanie metodą zaliczania danego zdania do konkretnej klasy.
Pierwszym w dziejach myśli europejskiej logicznym, tego rodzaju, systemem był zbudowany przez Arystotelesa tzw. rachunek nazw, zwany też sylogistyką Arystotelesa.
Sylogistyka: oznacza schemat wnioskowania pośredniego z dwu zdań kategorycznych złożony z dwu przesłanek, w których powtarza się ten sam termin oraz z konkluzji (wniosku) zbudowanej z pozostałych dwóch terminów występujących w przesłankach.
W sylogistyce tej formułuje się związki między zdaniami kategorycznymi o postaci:
Każde S jest P,
Niektóre (pewne) S są P,
Żadne S nie jest P,
Niektóre (pewne) S nie są P.
Używając symboli a, i, e, o jako stałych logicznych występujących w zdaniach kategorycznych zapisuje się podane wyżej wyrażenia w następującej postaci:
S a P ≡ (każde S jest P) ≡ (nie istnieje S nie będące P)
S i P ≡ (niektóre S są P) ≡ (istnieje S będące P)
S e P ≡ (żadne S nie jest P) ≡ (nie istnieje S nie będące P)
S o P ≡ (niektóre S nie są P) ≡ (istnieją S nie będące P)
Dla tych czterech klas zdań przysługują nazwy:
zdania ogólnotwierdzące,
zdania szczegółowotwierdzące,
zdania ogólnoprzeczące,
zdania szczegółowoprzeczące.
Symbole S, P, M, … występujące w takich wyrażeniach są zmiennymi nazwowymi, są nazwami cech (własności) obiektów, czyli predykatami jedno-argumentowymi.
Podział zdań kategorycznych na twierdzące i przeczące nazywa się podziałem tych zdań ze względu na jakość.
Definicja 1. Dwa zdania kategoryczne nazywa się zdaniami o tej samej jakości wtedy i tylko wtedy, gdy bądź oba są zdaniami twierdzącym, bądź oba są zdaniami przeczącymi.
Definicja 2. Dwa zdania mają przeciwną jakość, gdy jedno z nich jest twierdzące, a drugie przeczące.
Podział zdań kategorycznych na ogólne i szczegółowe nazywa się podziałem tych zdań ze względu na ilość.
Definicja 3. Dwa zdania kategoryczne nazywają się zdaniami o tej samej ilości wtedy i tylko wtedy, gdy bądź oba są ogólne, bądź oba są szczegółowe.
Definicja 4. Dwa zdania kategoryczne są zdaniami o różnej ilości, gdy jedno z nich jest ogólne, drugie jest szczegółowe.
Choć są zaledwie cztery kategorie zdań, to wynika z nich znaczna liczba praw wyrażonych za pomocą (≡ i →). Oto niektóre z nich:
S a P ≡ ~ S o P
S a P ≡ ~ S i P
S i P ≡ ~ S e P
S o P ≡ ~ S a P
Dla tych praw można podać następującą interpretację: dane zdanie kategoryczne jest prawdziwe wtedy i tylko wtedy, gdy zdanie z nim sprzeczne jest fałszywe, a więc gdy jego negacja jest prawdziwa. Następnie, jeśli jedno ze zdań przeciwnych jest prawdziwe, to drugie jest fałszywe (przyjmujemy niepustość zbioru, do elementów którego odnoszą się S, ~ S, P, ~ P), a więc jego negacja jest prawdziwa. Otrzymujemy więc dalsze następujące prawa dotyczące zdań przeciwnych:
S a P → S e P
S e P → S a P.
Uwaga. Dwa zdania przeciwne nie mogą być zarazem prawdziwe, ale mogą być zarazem fałszywe. Ponadto dwa zdania ogólne o tych samych podmiotach i o tych samych orzecznikach tworzą parę zdań przeciwnych, przy czym termin występujący na miejscu S nazywa się podmiotem, a termin stojący na miejscu zmiennej P nazywa się orzecznikiem zdania.
Dwa zdania szczegółowe o tych samych podmiotach i o tych samych orzecznikach tworzą parę zdań podprzeciwnych:
~ S i P → S o P
~ S o P → S i P.
Dwa zdania podprzeciwne nie mogą być zarazem fałszywe, ale mogą być zarazem prawdziwe.
Zdanie szczegółowe jest podporządkowane zdaniu ogólnemu o tej samej jakości oraz o tym samym podmiocie i o tym samym orzeczniku. Zatem jeśli prawdziwe jest zdanie ogólne, to z uwagi na niepustość jego podmiotu - prawdziwe jest zdanie jemu podporządkowane. Mamy prawa:
S a P → S i P
S e P → S o P.
S i P przysługują pewne zakresy, jeśli nazwy S i P są niepuste. Zatem między zakresami dwóch niepustych nazw S oraz P zachodzi jeden i tylko jeden z następujących stosunków zakresowych:
Nazwa S jest zamienna z nazwą P, zakresy nazw S oraz P są identyczne.
Nazwa S jest podrzędna względem nazwy P, zakres nazwy S jest podzbiorem zakresu nazwy P.
Nazwa S jest nadrzędna względem nazwy P, zakres nazwy P jest podzbiorem zakresu nazwy S.
Nazwa S krzyżuje się z nazwą P, zakresy nazw S i P mają część wspólną.
Nazwa S wyklucza się z nazwą P, zakresy nazw S oraz P są rozłączne.
Te stosunki zakresowe można symbolizować za pomocą diagramu Eulera i zaznaczać, przy jakich stosunkach zakresowych prawdziwe są poszczególne zdania kategoryczne. Rysunek 4. przedstawia to graficznie.
Rys.4. Zakresy nazw oraz prawa dla S i P.
Wszystkie prawa dla zdań kategorycznych można ująć w postaci tzw. kwadratu logicznego.
Rys.5. Kwadrat logiczny zdań S i P.
Niech teraz zbiór X reprezentuje elementy (obiekty) mające cechy S i P, bądź S i ~ P, itd., wówczas zdaniom kategorycznym 1 - 4 odpowiadają w zapisie logiki predykatorów wyrażenia:
∀ x [S(x) → P(x)], (każde S jest P)
∃ x [S(x) ∧ P(x)], (niektóre S są P)
∀ x [S(x) → ~ P(x)], (żadne S nie jest P)
∃ x [S(x) ∧ ~ P(x)], (niektóre S nie są P).
Przykłady:
Wszystkie romby są czworokątami.
Niektóre czworokąty są kwadratami.
Żadna liczba nieparzysta nie jest podzielna przez dwa.
Niektóre czworokąty nie są rombami.
Stosując podejście semantyczne można powyższe treściowe zdania przekształcić w wypowiedzi równoważne im, a następnie zapisywać je syntaktycznie i tworzyć prawa jednoargumentowych predykatów. Można też prawa sylogistyki Arystotelesa tłumaczyć na język logiki predykatów.
Z tej krótkiej analizy widać wyraźnie, że język logiki predykatów jest bogatszy od symboliki sylogistyki Arystotelesa. Co więcej zdania sylogistyki Arystotelesa stanowią bardzo wąski wycinek możliwych do utworzenia zdań jednoargumentowych w logice predykatów.
Powstaje jednak pytanie, jak w języku rachunku predykatów tworzyć jego wyrażenia i sprawdzać, które z nich są prawami, a które nie są, które są poprawnie zbudowane, a które nie są, itd.
Wyrażenia poprawnie zbudowane rachunku kwantyfikatorów
Definicja. Wyrażeniami poprawnie zbudowanymi rachunku kwantyfikatorów są wszystkie wyrażenia atomiczne (atomowe) rachunku zdań, a więc litery
p, q, r, …
Wyrażeniami poprawnie zbudowanymi są też wyrażenia zbudowane z liter P, Q, R, …, po których bezpośrednio występują litery x, y, z, … ujęte w nawiasy, np. wyrażenia
P(x), Q(x), P(y), Q(y), R(x, y), R(x, x), …
Wyrażenia te nazwaliśmy już wyrażeniami atomicznymi rachunku predykatów (kwantyfikatorów).
Jeśli wyrażenie a jest poprawnie zbudowane i w wyrażeniu tym występuje zmienna wolna x, to wyrażenia
∀ x (a), ∃ x (a)
są poprawnie zbudowane (zamiast o zmiennej x, może tu być mowa o dowolnej innej zmienne y, z, u, v, …).
Jeśli wyrażenia a i b są poprawnie zbudowane, to również wyrażenia
a ∧ b, a ∨ b, a → b, a ≡ b, ~a
są poprawnie zbudowane.
Żadne wyrażenie nie będące wyrażeniem atomicznym i które nie daje się otrzymać z wyrażeń atomicznych przez zastosowanie raz jeden lub kilka razy sposobów budowania wyrażeń złożonych, podany w punktach 2. i 3., nie jest wyrażeniem poprawnie zbudowanym.
Przykłady:
Wyrażenie
(1). ∀ x [P(x) → q] ∧ ~ R(y)
jest poprawnie zbudowane, bowiem spełnia warunki definicji.
Wyrażenie
(2). ∃ y [P(x) → ∀ y Q(y)]
nie jest poprawnie zbudowane, pomimo, że wyrażenie
(3). P(x) → ∀ y Q (y)
jest poprawnie zbudowane, gdyż w wyrażeniu tym nie występuje zmienna wolna y, będąca wskaźnikiem kwantyfikatora występującego na początku wyrażenia. Wyrażenie (3) nie spełnia warunku 4. definicji.
Podstawianie za zmienne w rachunku kwantyfikatorów
Czynność podstawiania w wyrażeniach matematycznych wykonuje się bardzo często. Ogólnie podstawianie można określić, jako zastępowanie jednych wyrażeń przez drugie. Spełniony przy tym zawsze musi być warunek, że wszystkie jednakowe części danego wyrażenia, za które wolno podstawić, zastępowane są przez to samo wyrażenie. Wyrażenie, które powstaje z danego wyrażenia przez podstawienie nazywamy jego podstawieniem. Jak przekonamy się niebawem, podstawienie w wyrażeniach, w których występują kwantyfikatory, nie jest czynnością prostą.
Wyrażenie otrzymane z danego wyrażenia przez podstawnie jest jego szczególnym przypadkiem, więc podstawienie wyrażenia prawdziwego jest zawsze wyrażeniem prawdziwym.
Z arytmetyki liczb rzeczywistych
∃ x (x ⋅ y ≠ 0) → (y ≠ 0)
otrzymujemy przez podstawienie nazwy 5 za zmienną wolną y wyrażenie
∃ x (x ⋅ 5 ≠ 0) → 5 ≠ 0,
będące szczególnym przypadkiem wyrażenia (1). Liczba 5 jest oczywiście liczbą rzeczywistą, należy więc do zakresu zmiennej y.
Zauważmy, że w wyrażeniu (1) nie możemy podstawiać za literę x, nie będącą w tym wyrażeniu zmienną wolną, zastępując bowiem w symbolu ∃ x wskaźnik x, np. nazwą 2 otrzymujemy zlepek symboli ∃ 2, nie mający sensu.
Nie jest też poprawnie zbudowane wyrażenie
∃ x (2y ≠ 0) → (y ≠ 0),
gdyż w wyrażeniu 2y ≠ 0 nie występuje zmienna wolna x, wyrażenie więc ∃ x (2y ≠ 0) nie spełnia warunku 2. definicji wyrażenia poprawnie zbudowanego.
Podany przykład uzasadnia następującą uwagę:
Uwaga 1. W wyrażeniach rachunku predykatów (również w wyrażeniach matematycznych tego rachunku) podstawiamy tylko za zmienne wolne. Podstawiane nazwy powinny oznaczać przedmioty należące do zakresu zmiennej, za którą podstawiamy.
Ponadto w podstawianym wyrażeniu a podstawiamy za zmienną wolną formę (wyrażenie) nazwową wtedy tylko, gdy zmienna ta nie występuje w wyrażeniu a w zasięgu kwantyfikatora, wiążącego jakąkolwiek zmienną występującą w podstawianej formie.
Biorąc raz jeszcze wyrażenie (1)
∃ x (x ⋅ y ≠ 0) → (y ≠ 0),
widzimy, że zgodnie z powyższą uwagą nie wolno za zmienną y podstawić zmiennej x będącej w tym wyrażeniu w zasięgu kwantyfikatora, czyli wyrażenie
(2) ∃ x (x ⋅ y ≠ 0) → (x ≠ 0)
nie jest szczególnym przypadkiem wyrażenia (1), lecz (2) jest wyrażeniem o innym sensie w stosunku do (1).
W wielu wyrażeniach rachunku predykatów często ta sama litera (zmienna) występuje raz jako zmienna związana, drugi raz - jako zmienna wolna:
(3) ∀ x (x2 ≥ 1) → (x2 ≥ 1).
W wyrażeniach takich, zgodnie z tym, że wolno podstawiać tylko za zmienne wolne, za zmienną x podstawiamy nazwy i formy nazwowe tam tylko, gdzie zmienna ta jest wolna. Podstawieniami do (3) są np. wyrażenia:
∀ x (x2 ≥ 1) → (32 ≥ 1), ∀ x (x2 ≥ 1) → [(x3 + 1)2 ≥ 1].
Definicja. Wyrażenie (matematyczne) jest podstawieniem wyrażenia rachunku predykatów wtedy i tylko wtedy, gdy powstaje z niego przez zastąpienie wszystkich jego zdań (p, q, …) i wyrażeń atomicznych (P (x), R(x, y), …) zdaniami lub formami zdaniowymi danego działu nauki (matematyki). Zastępowanie to powinno spełniać warunki omówione powyżej.
Do definicji tej dodajemy jeszcze uwagę.
Uwaga 2. W wyrażeniu a rachunku kwantyfikatorów zastępujemy wyrażenie atomiczne tego rachunku przez dowolną formę zdaniową jakiegoś działu nauki (matematyki), gdy w formie tej występują jako zmienne wolne wszystkie zmienne wyrażenia zastępowanego, przy czym mogą w niej występować też inne zmienne wolne, o ile nie są one związane w wyrażeniu a przez kwantyfikator, w zasięgu którego znajduje się zastępowane wyrażenie.
Np. mamy dane wyrażenie
(4) P(x) → ∀ y [Q(y) → P(x)].
Zastępując w wyrażeniu (4) P(x) i Q(y) odpowiednio przez x > y i y = 0 (pierwsze z zastąpień nie spełnia warunku w uwadze 2.) otrzymujemy wyrażenie
(x > y) → ∀ y [(y = 0) → (x > y)]
nie będące szczególnym przypadkiem wyrażenia (4) i nie będące wyrażeniem prawdziwym, pomimo, że każde wyrażenie pojedyncze podstawione do (4) jest poprawne.
Prawa i reguły rachunku kwantyfikatorów
Definicja. Wyrażenie rachunku kwantyfikatorów jest prawem tego rachunku wtedy i tylko wtedy, gdy każde podstawienie tego wyrażenia jest wyrażeniem prawdziwym.
Zakłada się przy tym, że zakresami wszystkich zmiennych danego prawa rachunku kwantyfikatorów są dowolne, lecz ustalone zbiory.
P1. ∀ x P(x) → P(x)
P2. P(x) → ∃ x P(x)
P3. ~ ∀ x P(x) ≡ ∃ x (~ P(x))
P4. ∀ x [P(x) → Q(x)] → [∀ x P(x) → ∀ x Q(x)]
P5. ∀ x [P(x) → Q(x)] → [∃ x P(x) → ∃ x Q(x)]
P6. ∀ x [P(x) ∧ Q(x)] ≡ [∀ x P(x) ∧ ∀ x Q(x)]
P7. ∃ x [P(x) ∧ Q(x)] → [∃ x P(x) ∧ ∃ x Q(x)]
P8. [∀ x P(x) ∨ ∀ x Q(x)] → ∀ x [P(x) ∨ Q(x)]
P9. ∃ x [P(x) ∨ Q(x)] → [∃ x P(x) ∨ ∃ x Q(x)]
P10. ∀ x [P(x) ≡ Q(x)] → [∀ x P(x) ≡ ∀ x Q(x)]
P11. ∀ x [P(x) ≡ Q(x)] → [∃ x P(x) ≡ ∃ x Q(x)]
P12. ∀ x [p → Q(x)] ≡ [p → ∀ x Q(x)]
P13. [∃ x Q(x) → p] ≡ ∀ x [Q(x) → p]
P14. ∃ x ∀ y R (x, y) → ∀ y ∃ x R (x, y)
∃ x ∀ y (x ⋅ y = y) → ∀ y ∃ x (x ⋅ y = y).
Definicja powyższa prawa rachunku kwantyfikatorów nie wyjaśnia jednak, jak prawa tworzyć, a sprawdzanie przez podstawienie może okazać się złudne, gdyż podstawień takich może być teoretycznie nieskończenie wiele. Omówiona metoda sprawdzania za pomocą tabelek jest pracochłonna i dotyczy ona tylko wyrażeń jednoargumentowych rachunku predykatów. Dlatego też, podobnie jak w rachunku zdań, rachunek predykatów (kwantyfikatorów) ujmuje się aksjomatycznie lub wyraża się systemem założeniowym. Omówimy ogólnie system założeniowy.
Dla otrzymania założeniowego systemu rachunku kwantyfikatorów przyjmujemy reguły pierwotne założeniowego systemu rachunku zdań - w odpowiednio rozszerzonej interpretacji - i wzbogacamy je o reguły pierwotne dla kwantyfikatorów. Ta rozszerzona interpretacja polega na tym, że termin wyrażenie zdaniowe występujący w formułowaniu tych reguł, rozumiemy obecnie jako termin oznaczający dowolne wyrażenie zdaniowe rachunku predykatów (I rzędu). Ta sama interpretacje przenosi się na reguły i tezy wtórne tego rachunku, w których za zmienne zdaniowe można podstawiać dowolne wyrażenia rachunku kwantyfikatorów zgodnie z zasadami podanymi w poprzednim punkcie.
Dodatkowymi regułami pierwotnymi dla rachunku kwantyfikatorów, którymi wzbogacamy tak rozumiane reguły pierwotne systemu założeniowego, są reguły dołączania i opuszczania kwantyfikatora ogólnego i szczegółowego.
Przyjmujemy następujące ogólne oznaczenia: wyrażenie zdaniowe F powstaje z wyrażenia zdaniowego E przez podstawienie wyrażenia W za zmienną wolną ν - zgodnie z opisanymi zasadami podstawiania.
Reguła opuszczania kwantyfikatora ogólnego oznaczana symbolem O∀ stwierdza, że z wyrażenia ∀ ν E wynika wyrażenie E (ν/W). Można ją zapisać w postaci schematu OA:
∀ ν E
E (ν/W)
Przykładami tego schematu są poniższe podstawienia:
∀ x P(x) |
|
∀ x P(x) |
|
∀ x P(x) |
|
∀ x R(x, y) |
|
∀ x p |
P(x) |
|
P(y) |
|
P(a) |
|
R(y, y) |
|
p |
Według reguły opuszczania kwantyfikatora ogólnego stąd, że każdy przedmiot ma pewną własność lub jest w relacji do innego przedmiotu, wynika, że dowolny, czy też pewien określony przedmiot ma tę własność.
Reguła dołączania kwantyfikatora ogólnego, oznaczona symbolem D∀ stwierdza, że z wyrażeń Z, nie zawierających zmiennej wolnej ν, wynika funkcja zdaniowa E(ν), w której ν jest zmienną wolną, to z wyrażeń Z wynika wyrażenie ∀ ν E(ν) oraz, że ∀ ν E wynika z E, jeśli ν nie jest wolne w E.
D∀ schematycznie zapisujemy:
Z (ν nie jest wolne w Z) E (ν nie jest wolne w E)
E(ν) ∀ ν E
∀ ν E(ν)
Sens tej reguły wyjaśnia poniższa uwaga: Jeśli z wyrażeń Z, nie zawierających zmiennej wolnej ν, wynika wyrażenie E(ν), to jeśli prawdziwe są wyrażenia Z, prawdziwe jest również wyrażenie E(ν), i to prawdziwe dla dowolnej wartości jego zmiennej wolnej ν, to i prawdziwe jest wówczas wyrażenie ∀ ν E(ν). Gdy natomiast E(ν) wynika z wyrażeń Z, zawierających zmienną wolną ν, to możemy stąd wnosić jedynie, że E(ν) jest prawdziwe dla tych wartości zmiennej wolnej, dla których prawdziwe są wyrażenia Z. Nie muszą to być jednak wszystkie wartości tej zmiennej, a więc wyrażenie E(ν) może być fałszywe.
Według D∀ w dowodzie założeniowym możemy dołączyć kwantyfikator ogólny do jakiegoś wiersza dowodu tylko wówczas, gdy zmienna związana przez ten kwantyfikator nie jest zmienną wolną w założeniach, ani zmienną wolną w założeniach dodatkowych wprowadzonych w dalszej części dowodu.
Np. z założenia (1) x > 2 wyprowadzamy wyrażenie (2) x > 2 ∨ x = 2, ale z (2) nie można wyprowadzić wyrażenia (3) ∀ x (x > 2 ∨ x = 2) za pomocą reguły D∀, gdyż zmienna x jest wolna w (1).
Uwaga. Do twierdzeń można stosować regułę D∀ bez ograniczeń, tj. można stosować ją do tez zawierających zmienne wolne. Reguły systemu założeniowego formułujemy bowiem w ten sposób, że każda teza tego systemu jest wyrażeniem prawdziwym. Jeśli zatem wyrażenie E, zawierające zmienną wolną ν, jest tezą, to jest ono prawdziwe, a więc spełnione przez każdy przedmiot (należący do zakresu zmiennej ν) przyporządkowany zmiennej wolnej ν. Wtedy prawdziwe jest wyrażenie ∀ ν E.
Np.
P(x) , x2 - y2 = (x - y) (x + y)
∀ x P(x) ∀ x ∀ y[x2 - y2 = (x - y) (x + y)]
Reguła dołączania kwantyfikatora szczegółowego (D∃) stwierdza, że z wyrażenia E(ν / W) wynika wyrażenie ∃ ν E. Zapis w postaci schematu:
E(ν / W)
∃ ν E
Oto kilka przykładów tego schematu:
A(x) |
|
A(y) |
|
P(a) |
|
P(y, y) |
|
P |
∃ x A(x) |
|
∃ y A(y) |
|
∃ x P(x) |
|
∃ x P(x, x) |
|
∃ x p |
a podstawieniami są schematy:
y2 ≥ 0 7 = 7 (x + y)2 + 2 > 0
∃ x (x2 ≥ 0) ∃ x (x = 7) ∃ x [(x + y)2 + 2 > 0]
Reguła opuszczania kwantyfikatora szczegółowego (O∃) stwierdza, że jeśli prawdziwe jest wyrażenie ∃ ν E(ν), to prawdziwe jest wyrażenie E(ν / a), a - stała wstawiana za zmienną ν.
Schematycznie:
∃ ν E (ν)
E (ν / a)
Na przykład:
∃ x P(x) ∃ x Q(x)
P(a) Q(b) .
Uwaga 1. Ponieważ w tezach rachunku kwantyfikatorów nie występują stałe indywiduowe, więc wyrażenia uzyskane za pomocą tej reguły O∃ nie mogą być tezami systemu. Mogą one jednak być wierszami założeniowymi dowodów takich tez.
Uwaga 2. Za każdym razem stosowania reguły opuszczania kwantyfikatora szczegółowego w tym samym dowodzie wprowadzamy nową stałą, różną od wszystkich stałych systemu i od stałych uprzednio wprowadzonych w tym dowodzie za pomocą tej reguły.
Przykłady założeniowych dowodów praw i reguł.
Reguła rozkładania kwantyfikatora na implikację.
∀ x [P(x) → Q(x)] |
∃ x P(x) → ∃ x Q(x) |
Dowód. (1) ∀ x [P(x) → Q(x)]
(2) ∃ x P(x) {zał.}
(3) P(a) {O∃: 2}
(4) P(a) → Q(a) {O∀: 1}
(5) Q(a) {RO:3, 4}
∃ x Q(x) {D∃: 5}.
Prawo rozkładania kwantyfikatora ogólnego
∀ x [P(x) ∧ Q(x) ≡ ∀ x P(x) ∧ ∀ x Q(x)
Dowód. (a) (1) ∀ x [P(x) ∧ Q(x)] {zał.}
(2) P(x) ∧ Q(x)] {O∀: 1}
(3) P(x)
(4) Q(x) {OK: 2}
(5) ∀ x P(x) {D∀: 3}
(6) ∀ x Q(x) {D∀: 4}
∀ x P(x) ∧ ∀ x Q(x) {DK: 5, 6}
Dowód. (b) (1) ∀ x P(x)
(2) ∀ x Q(x) {zał.}
(3) P(x) {O∀: 1}
(4) Q(x) {O∀: 2}
(5) P(x) ∧ Q(x) {DK: 3, 4}
∀ x [P(x) ∧ Q(x)] {D∀: 5}.
Reguła rozkładania kwantyfikatora szczegółowego na koniunkcję:
∃ x [P(x) ∧ Q(x)] |
∃ x P(x) ∧ ∃ x Q(x) |
Dowód. (1) ∃ x [P(x) ∧ Q(x)] {zał.}
(2) P(a) ∧ Q(a) {O∃: 1}
(3) P(a)
(4) Q(a) {OK: 2}
(5) ∃ x P(x) {D∃: 3}
(6) ∃ x Q(x) {D∃: 4}
∃ x P(x) ∧ ∃ x Q(x) {DK: 5, 6}
Według tej reguły ze zdania:
Istnieje taki x, że (x jest poetą i malarzem)
wynika zdanie:
(Istnieje taki x, że x jest poetą) i (istnieje taki x, że x jest malarzem).
Wynikanie odwrotne nie zachodzi.
Na koniec jako przykład udowodnimy prawo przestawiania kwantyfikatorów dla predykatu dwuargumentowego:
∃ x ∀ y R(x, y) → ∀ y ∃ x R(x, y)
Dowód. (1) ∃ x ∀ y R(x, y) {zał.}
(2) ∀ y R(a, y) {O∃: 1}
(3) R(a, y) {O∀: 2}
(4) ∃ x R(x, y) {D∃: 3}
∀ y ∃ x R(x, y) {D∀: 4}.
Po tych kilku przykładowych dowodach warto postawić pytanie, jak budować wyrażenia w logice kwantyfikatorów, aby były one tautologiami, bo sprawdzenie, czy np. formuła odwrotna do (1):
∀ y ∃ x R(x, y) → ∃ x ∀ y R(x, y)
jest prawdziwa, wymaga dość znacznych umiejętności, zwłaszcza, gdy są jeszcze w formułach dodatkowe funktory rachunku zdań.
Przejdziemy obecnie do omówienia powyższego problemu tworzenia tautologii za pomocą tabeli, która wyraża rozdzielność kwantyfikatorów względem funktorów zdaniotwórczych. Zagadnienie to daje się ująć syntetycznie w sposób następujący:
Niech ∗ oznacza którykolwiek z funktorów zdaniotwórczych ∨, ∧, →, ≡, znak T x - którykolwiek z kwantyfikatorów ∀ x lub ∃ x, a Φ(x) i Ψ(x) funkcje zdaniowe co najmniej jednej zmiennej x. Zagadnienie rozdzielności kwantyfikatorów względem funktorów zdaniotwórczych formułuje się następująco:
Czy i jaki z funktorów ≡, →, ← wstawiony w miejsce O w wyrażeniu
(*) T x [Φ(x) ∗ Ψ(x)] O [T x Φ(x) ∗ T x Ψ(x)]
zamienia je na tautologię rachunku kwantyfikatorów?
Odpowiedź na powyższe pytanie daje następująca tabelka:
Tabela 7.
|
Tx ∗ |
1 |
2 |
|
|
∀ x |
∃ x |
1 |
∨ |
← |
≡ |
2 |
∧ |
≡ |
→ |
3 |
→ |
→ |
← |
4 |
≡ |
→ |
|
W tabelce tej na przecięciu odpowiedniego wiersza (podyktowanego funktorem zdaniotwórczym) i kolumny (podyktowanej rodzajem kwantyfikatora) podano ten z funktorów ≡, →, ←, który wstawiony do wyrażenia (*) w miejsce O zamienia je na tautologię (← funktor ten też oznacza implikację od lewej strony wyrażenia do prawej).
Kratka (4, 2) tabelki (wiersz czwarty i kolumna druga), w której symbol
oznacza nie wynika, informuje nas, że w przypadku ≡ i ∃ x (w miejsce ∗ i T x w (*), wyrażenie (*) nie jest tautologią, niezależnie od tego, który z funktorów ≡, →, ← wstawimy w miejsce O.
Przykładowo kratka (2, 1) daje tautologię
∀ x [Φ(x) ∧ Ψ(x)] ≡ [∃ x Φ(x) ∧ ∃ x Ψ(x)],
a kratka (2, 2) tautologię
∃ x [Φ(x) ∧ Ψ(x)] → [∃ x Φ(x) ∧ ∃ x Ψ(x)].
Rachunek zbiorów i relacji
Podstawowym pojęciem dla naszych dalszych rozważań będzie pojęcie zbioru elementów, o których naturze (jakości) nie czynimy żadnych założeń. Tak więc elementami zbiorów mogą być liczby, figury geometryczne, a więc zbiory punktów, ludzi, funkcje, zwierząt, przesłanek, itp. Pojęcie zbioru przyjmuje się za pojęcie pierwotne, podobnie za pojęcie pierwotne przyjmuje się przynależność elementu do zbioru (relację). Relacja ta jest funkcją zdaniową: element a należy do zbioru A. Negację tej funkcji zdaniowej rozumiemy jako zwrot: element a nie należy do zbioru A.
Gdy a jest przedmiotem należącym do zbioru A, b zaś - przedmiotem, który do A nie należy, to fakt ten notujemy symbolicznie za pomocą wyrażeń:
a ∈ A, b ∉ A.
∈ - relacja przynależności a do zbioru A.
∉ - czytaj a nie należy do zbioru A.
Przedmioty należące do danego zbioru nazywamy jego elementami. Każdy zbiór jest jednoznacznie wyznaczony przez swoje elementy; tak więc, jeśli A i B są zbiorami, do których należą dokładnie te same elementy, to A i B są tym samym zbiorem. Jest to tzw. aksjomat jednoznaczności (patrz definicja pary).
Gdy wszystkimi elementami zbioru A są przedmioty a1, a2, … , an, to zbiór A oznaczamy symbolem:
{ a1, a2, … , an} - zbiór skończony,
przy czym kolejność w jakiej wymieniamy przedmioty a1, a2, … , an jest dowolna. W szczególności:
{a, b} = {b, a}.
Zbiór mający dokładnie jeden element nazywamy zbiorem jednostkowym. Zbiór nie mający żadnego elementu nazywamy zbiorem pustym i oznaczamy go symbolem ∅.
Elementami zbiorów mogą być również zbiory, na przykład, jeśli A jest dowolnym zbiorem, to wyrażenie {A} symbolizuje zbiór jednostkowy, którego elementem jest zbiór A. Oczywiście:
A ∈ {A}, lecz A ≠ {A}.
Przez zmienną indywiduową rozumiemy zmienną, która za swoje wartości może przyjmować obiekty.
Niech ϕ (x) będzie formą zdaniową zawierającą zmienną indywiduową x. Zbiór wszystkich obiektów spełniających formę zdaniową ϕ (x) oznaczać będziemy symbolem:
{x: ϕ (x)}.
Wyrażenie to czytamy: jest to zbiór tych wszystkich x-ów, dla których zachodzi (ma miejsce) funkcja zdaniowa ϕ (x).
Operacje na zbiorach
Sumą zbiorów A, B nazywamy zbiór, którego elementami są wszystkie elementy zbioru A lub wszystkie elementy zbioru B. Działanie sumy zbiorów oznaczamy symbolem ∪:
A ∪ B = {x : x ∈ A ∨ x ∈ B}.
Iloczynem (przekrojem, częścią wspólną) zbiorów A, B nazywamy zbiór, którego elementami są wszystkie i tylko te przedmioty, które są równocześnie elementami zbioru A i zbioru B. Działanie iloczynu zbiorów oznaczamy symbolem ∩:
A ∩ B = {x : x ∈ A ∧ x ∈ B}.
Różnicą zbioru A i zbioru B nazywamy zbiór, którego elementami są wszystkie i tylko te przedmioty, które są elementami zbioru A, a nie są elementami zbioru B. Działanie różnicy oznaczamy symbolem \:
A \ B = {x : x ∈ A ∧ x ∉ B}
lub
A \ B = {x : (x ∈ A ∨ x ∈ B) ∧ ~ (x ∈ B)}.
Obie definicje są równoważne.
Inkluzją (zawieranie się zbiorów). Jeżeli każdy element zbioru A jest zarazem elementem zbioru B, to mówimy, że zbiór A zawiera się w zbiorze B, co zapisujemy symbolicznie A ⊂ B. Mamy więc:
A ⊂ B = {x : (x ∈ A) → (x ∈ B)}.
Za pomocą inkluzji można zdefiniować równość zbiorów.
(A = B) ![]()
{A ⊂ B ∧ B ⊂ A}.
Inkluzja między zbiorami ma następujące własności:
A ⊂ A dla każdego zbioru A (jest to tzw. zwrotność inkluzji)
[(A ⊂ B) ∧ (B ⊂ C)] → (A ⊂ C) dla każdych trzech zbiorów A, B i C (tzw. przechodniość inkluzji)
φ ⊂ A dla każdego zbioru A.
Dla przykładu udowodnimy własność
[(A ⊂ B) ∧ (B ⊂ C)] → (A ⊂ C).
Dowód. Niech a ∈ A. Wtedy wobec A ⊂ B = {x: (x ∈ A) →(x ∈ B)} mamy a ∈ B. Ponieważ B ⊂ C, więc także a ∈ C. Tak więc dla dowolnego a
(a ∈ A) → (a ∈ C), czyli A ⊂ C,
co należało wykazać.
Jeżeli przyjrzymy się definicji inkluzji, to można powiedzieć, że dowód własności inkluzji oparty był o schemat logicznego wnioskowania postaci:
p → q |
q → r |
p → r |
gdzie
p → q odpowiada A ⊂ C |
q → r odpowiada B ⊂ C |
p → r odpowiada A ⊂ C |
W algebrze zbiorów opartej o wprowadzone działania na zbiorach przyjmuje się często pewien zbiór, zwany zbiorem pełnym lub przestrzenią uniwersalną (oznacza się np. symbolem V), poza który w jej rozważaniach nie wychodzi się, tzn. ogranicza się jedynie do zbiorów o elementach z tego zbioru V.
Aksjomat zbioru potęgowego. Dla każdego zbioru A istnieje zbiór, którego elementami są wszystkie zbiory zawarte w zbiorze A.
Zbiór wszystkich podzbiorów zbioru A oznaczamy przez 2A (stąd nazwa aksjomatu). Do roli tego aksjomatu i przestrzeni V odwołamy się jeszcze w dalszych naszych rozważaniach.
Dopełnieniem ![]()
zbioru A nazywamy zbiór wszystkich elementów przestrzeni V, które nie należą do A, a więc
![]()
= V \ A
Graficzna reprezentacja zbiorów.
Wprowadzone powyżej zbiory możemy zilustrować graficznie. Niech A i B będą zbiorami punktów na płaszczyźnie, leżących wewnątrz i na okręgach zakreskowanych kół (rys. 1.). A - koło zakreskowane poziomo, B - pionowo. Wtedy suma A ∪ B jest zbiorem punktów należących do jednego z tych kół lub do drugiego z tych kół, a więc zbiorem punktów zakreskowanym jakkolwiek, tzn. pionowo, poziomo lub w kratkę (bo mogą mieć wspólne elementy). Iloczyn A ∩ B stanowi zbiór zakreskowany w kratkę, A \ B jest zbiorem punktów należących do koła A, a nie należących do koła B, czyli zbiorem punktów zakreskowanych tylko poziomo, B \ A jest zbiorem punktów zakreskowanym tylko pionowo, ![]()
to zbiór punktów płaszczyzny będącej tu przestrzenią V nie należących do zbioru A, a więc zbiór punktów zakreskowany tylko pionowo lub nie zakreskowany w ogóle, analogicznie ![]()
to zbiór punktów płaszczyzny zakreskowany tylko poziomo lub nie zakreskowany w ogóle.
Rys.1. Ilustracja graficzna działań na zbiorach.
Algebra zbiorów
Określone powyżej działania na zbiorach mają cały szereg własności analogicznych do własności działań na liczbach. Dlatego dział zajmujący się tymi własnościami nazywa się algebrą zbiorów. Algebrę tę utworzył irlandzki matematyk George Boole (1815 - 1864).
I tak działania dodawania i mnożenia zbiorów są:
a). przemienne, tzn.
A ∪ B = B ∪ A oraz A ∩ B = B ∩ A
dla każdych dwóch zbiorów A i B.
b). łączne, tzn.
(A ∪ B) ∪ C = A ∪ (B ∪ C)
oraz
(A ∩ B) ∩ C = A ∩ (B ∩ C)
dla każdych trzech zbiorów A, B i C.
Mnożenie jest rozdzielne względem dodawania, tzn.
c). (A ∪ B) ∩ C = A ∩ C) ∪ (B ∩ C)
dla każdych trzech zbiorów A, B i C.
Przeprowadzimy przykładowo dowód ostatniego związku: mamy
(A ∪ B) ∩ C = {x : x ∈ [(A ∪ B) ∩ C] = {x : x ∈ (A ∪ B) ∧ x ∈ C} =
= {x : [(x ∈ A) ∨ (x ∈ B)] ∧ (x ∈ C)} =
= {x : [(x ∈ A) ∧ (x ∈ C)] ∨ [(x ∈ B) ∧ (x ∈ C)]} =
= {x : x ∈ (A ∩ C) ∨ (x ∈ (B ∩ C)} =
= {x : x ∈ (A ∩ C)} ∨ {x: x ∈ (B ∩ C)} = (A ∩ C) ∪ B ∩ C).
Udowodniony związek możemy też zilustrować graficznie na znanym nam już schemacie kołowym (rys. 2).
A - kreski poziome
B - kreski pionowe
C - kreski ukośne
Rys.2. Ilustracja graficzna własności c) dla zbiorów.
A ∪ B - część rysunku zakreskowana poziomo lub pionowo,
(A ∪ B) ∩ C - część zakreskowana ukośnie i zarazem pionowo i poziomo (część zakreskowana w ukośną kratkę),
A ∩ C - część zakreskowana poziomo i ukośnie
B ∩ C - część zakreskowana pionowo i ukośnie
i wreszcie
(A ∩ C) ∪ (B ∩ C) - część zakreskowana poziomo i ukośnie lub pionowo i ukośnie, a więc tak samo jak zbiór (A ∪ B) ∩ C.
Zbiór ten na rysunku 2 obwiedziony jest grubszą kreską.
Zauważmy, że
d). zbiór pusty jest modułem dla dodawania (odgrywa rolę zera w dodawaniu liczb), czyli
A ∪ ∅ = A
dla każdego zbioru A.
e). cała przestrzeń V jest modułem dla mnożenia (odgrywa rolę jedynki przy mnożeniu liczb), czyli
A ∩ V = A
dla każdego zbioru A.
Działania na zbiorach mają jednak też własności takie, których analogony dla liczb nie są prawdziwe. Do takich należą:
f). prawo rozdzielności dodawania względem mnożenia, tzn.
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
dla każdych trzech zbiorów A, B i C.
g). prawo idempotentności dodawania i mnożenia, tzn.
A ∪ A = A oraz A ∩ A = A
dla każdego zbioru A.
h). wyrażenie mnożenia przez odejmowanie
A ∩ B = A \ (A \B)
dla każdych dwóch zbiorów A i B, świadczące o tym, że mnożenie można zdefiniować przez odejmowanie.
i). prawo de Morgana z algebry zbiorów:
![]()
= ![]()
∩ ![]()
oraz ![]()
= ![]()
∪ ![]()
dla każdych dwóch zbiorów A i B.
j). (A ∪ B = A) ≡ (A ∩ B ≡ B) ≡ (B ⊂ A)
dla każdych dwóch zbiorów A i B.
Graficznie przedstawia to poniższy rysunek
Rys. 3. Graficzna ilustracja własności j).
Stąd, ponieważ (A ∩ B = B) ≡ B ⊂ A, to zachodzi też
k). A ∩ B ⊂ A
dla każdego zbioru A i B,
więc
l). A ∪ (A ∩ B) = A
dla każdego zbioru A i B,
m).
A ∪ ![]()
= V oraz A ∩ ![]()
= ∅
dla każdego zbioru A,
n). A \ B = A ∩ ![]()
dla każdych dwóch zbiorów A i B.
Dzięki tym i analogicznym twierdzeniom - które możemy wykazać i zinterpretować analogicznie jak związek c) - możemy na zbiorach rachować, jak na liczbach.
Zilustrujemy to pokazując, jak z twierdzeń c), g), k), a) (w kolejności ich stosowania) otrzymujemy związek f). Mamy:
(A ∪ B) ∩ (A ∪ C) = [A ∩ (A ∪ C)] ∪ [B ∩ (A ∪ C)] =
= (A ∩ A) ∪ (A ∩ C) ∪ (B ∩ A) ∪ (B ∩ C) =
= A ∪ (A ∩ C) ∪ (B ∩ A) ∪ (B ∩ C) = A ∪ (B ∩ A) ∪ (B ∩ C) =
= A ∪ (B ∩ C).
Dla pełniejszego obrazu stosunku algebry liczb do algebry zbiorów warto zauważyć, że pewne twierdzenia prawdziwe w algebrze liczb, przestają być prawdziwe po przetłumaczeniu ich na język algebry zbiorów.
Przykład. Wiemy, że jeśli (a ∗ b = 0), to (a = 0 lub b = 0).
Jest to twierdzenie prawdziwe na gruncie np. liczb rzeczywistych, a fałszywe w algebrze zbiorów w następującym sformułowaniu:
Jeśli (A ∩ B = ∅), to (A = ∅ lub B = ∅), dwa zbiory mogą bowiem być rozłączne, choć żaden z nich nie jest zbiorem pustym, np. zbiór liczb wymiernych i zbiór liczb niewymiernych.
Definicja pary. Iloczyn kartezjański
W matematyce i nie tylko, często występuje pojęcie pary elementów. Pierwiastkiem układu równań o dwu niewiadomych jest para liczb, punkt na płaszczyźnie, na której jest dany punkt odniesienia, ma parę współrzędnych, itp. Dlatego w wielu rozważaniach pojęcie pary ma ważne znaczenie. Zdefiniujemy obecnie pojęcie pary za pomocą pojęcia zbioru. W tym miejscu należy przypomnieć, że zbiór złożony z elementów a, b, c, … umówiliśmy się oznaczać symbolem {a, b, c, …}. Zbiory {a, b} i {b, a} są sobie równe, składają się bowiem z tych samych elementów. Równość zbiorów wyznacza tzw. Aksjomat jednoznaczności. Jeżeli zbiory A i B mają te same elementy, to zbiory te są równe.
Przyjmujemy następującą definicję pary o pierwszym elemencie a i drugim b (symbolicznie <a, b〉).
Definicja. Parą <a, b〉 nazywamy zbiór, którego elementami są: zbiór złożony z elementu a oraz zbiór o elementach a i b. Symbolicznie zapisujemy tę definicję następująco:
<a, b〉![]()
{{a}, {a, b}}.
Gdy a = b, to {a, b} = {a}
a para
<a, b〉 = {{a}, {a, b}} = {{a}, {a}} = {{a}}
jest zbiorem złożonym z jednego elementu, którym jest zbiór utworzony z elementu a.
Podstawową własnością tak zdefiniowanej pary elementów jest następująca równoważność:
(*) [<a, b〉 = <c, d〉 ≡ [(a = c) ∧ (b = d)],
słownie: dwie pary są równe wtedy i tylko wtedy, gdy ich pierwsze elementy są równe i drugie elementy są równe.
Podobnie możemy zdefiniować trójkę elementów <a, b, c〉:
<a, b, c〉 ![]()
{{a}, {a, b}, {a, b, c}}
i ogólnie układ n elementów <a1, a2, …, an〉.
<a1, a2, …, an〉 ![]()
{{a1}, {a1, a2}, {a1, a2, a3}, …, { a1, a2, …, an}}
Dla układu n elementów zachodzi następująca równoważność - gdy n = 2 - równoważność (*):
[<a1, a2, …, an〉 = <b1, b2, …, bn〉] ≡ [ai = bi, dla i ∈ {1, 2, …, n}].
Niech będą dane dwa zbiory A i B. Iloczyn kartezjański A ![]()
B tych zbiorów definiujemy następująco:
A ![]()
B ![]()
{<a, b〉 : ((a ∈ A) ∧ (b ∈ B))},
Tzn. jest to zbiór tych wszystkich par, których pierwsze elementy należą do zbioru A, a drugie elementy do zbioru B.
Przykład 1. Prostoliniowy układ odniesienia na płaszczyźnie ustala odpowiedniość wzajemnie jednoznaczną między punktami tej płaszczyzny, a iloczynem kartezjańskim zbioru liczb rzeczywistych przez zbiór liczb rzeczywistych, czyli - jak mówimy - drugą potęgą kartezjańską (R ![]()
R = R2) zbioru liczb rzeczywistych.
Iloczyn kartezjański jest rozdzielny względem dodawania, odejmowania i mnożenia zbiorów, tzn. zachodzą wzory następujące:
(A ∪ B)![]()
C = (A ![]()
C) ∪ (B ![]()
C),
(A \ B) ![]()
C = (A ![]()
C) \ (B ![]()
C),
(A ∩ B) ![]()
C = (A x C) ∩ (B ![]()
C),
C ![]()
(A ∪ B) = (C ![]()
A) ∪ (C ![]()
B),
C ![]()
(A \ B) = (C ![]()
A) \ (C ![]()
B),
C ![]()
(A ∩ B) = (C ![]()
A) ∩ (C ![]()
B),
dla każdych trzech zbiorów A, B i C.
Dla przykładu uzasadnimy ostatni z nich, mamy
C x (A ∩ B) = {<x, y〉 : [(x ∈ C ∧ (y ∈ A ∩ B)]} =
= {<x, y〉 : [(x ∈ C) ∧ (y ∈ A) ∧ (y ∈ B)]} =
= {<x, y〉 : [(x ∈ C) ∧ (y ∈ A) ∧ (x ∈ C) ∧ (y ∈ B)]} =
= {<x, y〉: [<x, y) ∈ C ![]()
A)] ∧ [<x, y) ∈ C ![]()
A]} =
= {<x, y〉 : <x, y) ∈ (C ![]()
A) ∩ C ![]()
B]} = (C ![]()
A) ∩ (C ![]()
B).
Przyjmując za zbiory A, B i C przedziały w układzie kartezjańskim zbiorów liczb rzeczywistych i umieszczając przedział C na osi x, a przedziały A i B na osi y (rys.4) możemy udowodniony związek zinterpretować następująco: Zbiór C ![]()
(A ∩ B) jest prostokątem odwiedzionym grubą kreską, zbiory C ![]()
A, C ![]()
B są prostokątami zakreskowanymi poziomo i pionowo. Widoczne jest, że ich iloczyn mnogościowy (C x A) ∩ (C ![]()
B), czyli zbiór zakreskowany w kratkę, pokrywa się ze zbiorem grubo obwiedzionym, a więc ze zbiorem C ![]()
(A ∩ B).
Rys.4. Obraz graficzny prawa C ![]()
(A ∩ B) = (C ![]()
A) ∩ (C ![]()
B).
Z definicji pary uporządkowanej jasno wynika, że iloczyn kartezjański nie jest przemienny i nie jest łączny, tzn. wzory
A ![]()
B =B ![]()
A oraz (A ![]()
B) ![]()
C = A ![]()
(B ![]()
C)
nie są prawdziwe dla dowolnych zbiorów A, B i C. Mamy bowiem
Z1 ![]()
{a, b} ![]()
{a} = {<a, a〉, <a, b〉}
Z2 ![]()
{a} ![]()
{a, b} = {<a, a〉, <a, b〉},
a więc dla a ≠ b mamy Z1 ≠ Z2, bo <a, b〉 ∈ Z2, natomiast <a, b〉 ∉ Z2.
Podobnie dla A = {a}, B = {b}, C = {c} mamy:
A ![]()
B = <a, b〉}, (A ![]()
B) ![]()
C = {<<a, b〉, c〉},
B ![]()
C = {<b, c〉}, A ![]()
(B ![]()
C) = {<a, <b, c〉〉},
a więc nie zawsze (A ![]()
B) ![]()
C = A ![]()
(B ![]()
C).
Przyjmujemy, że a ≠ b ≠ c.
Relacje dwuczłonowe
Niech będą dane dwa zbiory A i B. Dowolny podzbiór R ich iloczynu kartezjańskiego A ![]()
B nazywamy relacją dwuczłonową. O elementach x i y pary <x, y〉 należącej do R mówimy, że pozostają w relacji R, co zapisujemy x R y lub R (x, y). Mamy więc
(*) <x, y〉 ∈ R ≡ x R y
Zauważmy, że na tle każdej funkcji zdaniowej dwu zmiennych ϕ (x, y) o zadanym polu A ![]()
B (A jest polem zmiennej x, B jest polem zmiennej y możemy utworzyć relację dwuczłonową
R ![]()
{<x, y〉 : ϕ (x, y)}
Uwaga: pojęcie pola możemy zastąpić często używanym pojęciem zakresu zmienności, którym są zbiory A i B. Wówczas mówimy, że ϕ (x, y) jest funkcją zdaniową dwóch zmiennych x i y, których zakresami zmienności odpowiednio są zbiory A i B. ϕ (x, y) staje się zdaniem, gdy zamiast zmiennej x podstawimy nazwę dowolnego elementu zbioru A, a zamiast y - dowolnego elementu zbioru B.
Funkcję zdaniową dwóch zmiennych x i y, których polami są odpowiednio zbiory A i B można traktować, jako funkcję zdaniową jednej zmiennej z = <x, y〉, której polem jest produkt kartezjański A ![]()
B.
Należy jeszcze wyraźnie podkreślić, że pojęcie relacji dwuczłonowej nie jest identyczne z pojęciem funkcji zdaniowej, pierwsza jest zbiorem, druga nie. Niektórym relacjom nadajemy i w życiu potocznym i w matematyce (szczególnie) pewne nazwy. Na niektóre relacje w matematyce przyjmuje się specjalne symbole (oznaczenia).
Jaką więc rolę pełni funkcja zdaniowa ϕ (x, y) w odniesieniu do relacji dwuczłonowej?
Wyjaśnimy to na przykładzie.
Niech X = Y = ℜ, gdzie ℜ jest zbiorem wszystkich liczb rzeczywistych. Wyrażenie x < y, x ∈ ℜ , y ∈ ℜ , jest przykładem funkcji zdaniowej dwóch zmiennych x i y, których zakresami zmienności (polami) są zbiory ℜ i ℜ .
Weźmy teraz pod uwagę dowolną funkcję zdaniową ϕ (x, y), x ∈ X, y ∈ Y. Będziemy mówić, że element <a, b〉 produktu X ![]()
Y spełnia tą funkcję zdaniową, jeżeli zdanie ϕ (x, y) jest prawdziwe. Dla naszego przykładu np. para <2, 5〉 spełnia funkcję zdaniową x < y, ponieważ zdanie 2 < 5 jest prawdziwe.
Ważne rodzaje relacji
Zaznaczyliśmy poprzednio, że niektóre relacje mają specjalne nazwy i oznaczenia. Nazwy te wiążą się z pewnymi ważnymi ich własnościami.
Relacja zwrotna. Relację dwuczłonową R ⊂ X ![]()
X nazywamy zwrotną, jeżeli dla każdego x ∈ X spełniony jest warunek
x R x
Przykłady:
Relacja identyczności w zbiorze X ≠ ∅ jest zwrotna, bowiem dla każdego x ∈ X mamy x = x. Relacja podzielności w zbiorze liczb naturalnych jest zwrotna, bowiem dla każdej liczby naturalnej x, x jest podzielne przez x. Relacja ≤ (mniejszości lub równości) w zbiorze liczb rzeczywistych jest zwrotna, ponieważ dla każdej liczby rzeczywistej x , zachodzi x ≤ x.
Relacja przeciwzwrotna. Relację R ∈ X ![]()
X nazywamy przeciw-zwrotną, jeśli dla żadnego x nie zachodzi x R x, czyli gdy
~ (x R x)
dla każdego x ∈ X.
Przykłady:
Relacja mniejszości w zbiorze liczb rzeczywistych jest przeciwzwrotna, ponieważ warunek x < x nie jest spełniony dla żadnej liczby rzeczywistej. Relacja ojcostwa w zbiorze ludzi jest przeciwzwrotna, bowiem żaden człowiek nie jest swoim ojcem.
Relacja symetryczna. Relację R ⊂ X ![]()
X nazywamy symetryczną, jeśli warunek x R y pociąga za sobą warunek y R x dla każdego x, y ∈ X. Symbolicznie zapisujemy to w następujący sposób:
x R y → y R x
dla każdego x, y ∈ X.
Przykłady:
Relacja identyczności w każdym zbiorze X ≠ ∅ jest relacją symetryczną, bowiem warunek x = y pociąga za sobą y = x. Relacja równoległości prostych w zbiorze wszystkich prostych na płaszczyźnie ℜ x ℜ jest symetryczna, ponieważ warunek L równoległa do Q pociąga za sobą Q równoległa do L dla każdej prostej L i Q.
Relacja przeciwsymetryczna (asymetryczna). Relację R ⊂ X ![]()
X nazywamy przeciwsymetryczną, jeśli warunek x R y pociąga ~ (y R x), czyli gdy warunki x R y i y R x wykluczają się nawzajem, dla każdych dwu elementów x, y zbioru X.
Przykłady:
Relacja większości w zbiorze liczb rzeczywistych jest przeciwsymetryczna, bowiem warunki x < y i y > x wykluczają się nawzajem dla każdej pary x i y liczb rzeczywistych.
Relacje R w zbiorze liczb naturalnych zachodzące pomiędzy x i y wtedy i tylko wtedy, gdy x = 2 y jest przeciwsymetryczna, bowiem warunki x = 2 y i y = 2 x dla każdej pary x, y liczb naturalnych wykluczają się nawzajem.
Relacja antysymetryczna. Relację R ⊂ X ![]()
X nazywamy antysyme-tryczną, jeśli warunki x R y i y R x pociągają za sobą warunek x = y dla każdej pary x, y elementów zbioru X. W postaci zbioru zapisujemy
(x R y ∧ y R x) → (x = y)
dla każdego x, y ∈ X.
Przykłady:
Relacja ≤ w zbiorze liczb rzeczywistych jest relacją antysymetryczną, bowiem warunki x ≤ y i y ≤ x pociągają za sobą warunek x = y dla każdej pary liczb rzeczywistych x, y. Relacja inkluzji C w dowolnej rodzinie zbiorów jest relacją antysymetryczną, bowiem warunki A ⊂ B i B ⊂ A pociągają za sobą warunek A = B dla każdej pary A, B zbiorów należących do tej rodziny.
Relacja przechodnia. Relację R ⊂ X ![]()
X nazywamy przechodnią, jeśli warunki x R y i y R x pociągają za sobą warunek x R z dla każdych trzech elementów x, y, z zbioru X. Symbolicznie zapisujemy to jak następuje:
(x R y ∧ y R z) → (x R z)
dla każdego x, y, z ∈ X.
Przykłady:
Relacja podzielności w zbiorze liczb naturalnych jest przechodnia, jeśli bowiem x jest dzielnikiem y i y jest dzielnikiem z, to x jest dzielnikiem z. Relacja inkluzji C w dowolnej rodzinie zbiorów jest przechodnia, jeśli bowiem A ⊂ B i B ⊂ C, to A ⊂ C dla każdych trzech zbiorów A, B, C należących do tej rodziny.
Między relacjami mogą zachodzić związki, które ujmowane są poprzez twierdzenia. Przykładowo następujące twierdzenie ustala związek pomiędzy relacjami przeciwzwrotnymi i przechodnimi a przeciwsymetrycznymi.
Twierdzenie. Każda relacja R ⊂ X ![]()
X przeciwzwrotna i przechodnia jest przeciwsymetryczna.
Dowód. Załóżmy, że relacja R ⊂ X ![]()
X jest przeciwzwrotna i przechodnia. Niech dalej dla pewnej pary x, y elementów zbioru X jest x R y i y R x. Z przechodniości relacji R wynika, że zachodzić musi x R x, co jest niemożliwe, bo R jest przeciwzwrotna. Zatem x R y i y R x wykluczają się nawzajem, co dowodzi, że R jest relacją przeciwsymetryczną.
Relacja spójna. Relację R ⊂ X ![]()
X nazywamy spójną w zbiorze X, jeśli spełnia ona warunek:
(x R y) ∨ (y R x) ∨ (x = y)
dla każdych dwóch elementów x, y ∈ X.
Bardziej przejrzystą definicję relacji spójnej można przedstawić za pomocą implikacji, a mianowicie mając alternatywę obiektów
(x = y) ∨ (x R y) ∨ (y R x)
możemy ją wyrazić równoważnie przez:
dla dowolnych dwóch elementów x, y ∈ X
~ (x = y) → [(x R y) ∨ (y R x)],
czyli
(x ≠ y) → [(x R y) ∨ (y R x)].
Przykłady.
Relacje <, >, ≤, ≥ w zbiorze liczb rzeczywistych są spójne. Wynika to również z tego, że dla dowolnych dwóch liczb rzeczywistych x, y ∈ R ma miejsce tzw. zasada trichotomii, tzn., że:
(*) (x < y) lub (x > y) lub (x = y).
Inaczej, jeśli (x ≠ y), to (x < y lub y < x), czyli (x jest w relacji R z y) lub (y jest w relacji R z x).
Relacje równoważności
Definicja. Relację R ⊂ X ![]()
X nazywamy relacją równoważności w zbiorze X, jeśli R jest relacją zwrotną, symetryczną i przechodnią, to znaczy jeśli spełnione są trzy następujące warunki:
(z) x R x, dla każdego x ∈ X,
(s) x R y → y R x, dla każdego x, y ∈ X,
(p) (x R y ∧ y R z) → x R z, dla każdego x, y, z ∈ X.
Relację równoważności oznacza się zazwyczaj symbolem ≈.
Przykłady: I. Niech R będzie zbiorem wszystkich liczb rzeczywistych i niech ≈ będzie dwuczłonową relacją w R zdefiniowaną w następujący sposób: dla dowolnych liczb rzeczywistych x, y relacja x ≈ y zachodzi wtedy i tylko wtedy, gdy x - y jest liczbą całkowitą. Niech Z będzie zbiorem wszystkich liczb całkowitych. Niech zatem
(x ≈ y) ≡ (x - y ∈ Z).
Tak zdefiniowana relacja jest relacją równoważności w R.
Wykażemy to.
Relacja ta jest zwrotna, bowiem x - x = 0 ∈ Z, a więc x ≈ x. Relacja ≈ jest symetryczna, gdyż jeśli x ≈ y, to x - y ∈ Z, stąd wynika, że y - x ∈ Z, bo y - x = - (x - y) ∈ Z, a więc y ≈ x. Relacja ≈ jest też przechodnia. Załóżmy, że x ≈ y i y ≈ z. Wynika stąd x - y ∈ Z i y - z ∈ Z. W konsekwencji x - z = (x - y) + (y - z) ∈ Z, czyli x ≈ z.
II. Niech L będzie zbiorem wszystkich prostych na płaszczyźnie euklidesowej ℜ2. Niech ≈ będzie dwuczłonową relacją w L , taką, że P ≈ Q dla dowolnych prostych P, Q należących do L wtedy i tylko wtedy, gdy prosta P jest równoległa do prostej Q. Relacja ta jest równoległa do prostej Q. Relacja ta jest więc relacją równoważności w zbiorze L.
Zbiory uporządkowane
Relacje porządkujące. Relację R ⊂ X ![]()
X nazywamy porządkującą zbiór X, jeśli jest zwrotna, przechodnia i antysymetryczna, czyli jeśli spełnia następujące warunki:
(z) x R x, dla każdego x ∈ X,
(p) (x R y ∧ y R z) → x R z, dla każdego x, y, z ∈ X,
(a) (x R y ∧ y R x) → x = y, dla każdego x, y ∈ X.
Zamiast x R y piszemy często x ≤ y i czytamy x jest zawarte w y lub też y zawiera x, albo x poprzedza y.
Relacje spełniające warunki (z), (p), (a) nazywane są relacjami częściowo porządkującymi zbiory.
Przykłady:
Niech A będzie dowolną niepustą rodziną podzbiorów zbioru X ≠ ∅. Niech R będzie relacją inkluzji w A. Relacja ta porządkuje A. Dla dowolnych zbiorów A< B, C należących do A mamy: A ⊂ A, jeśli A ⊂ B i B ⊂ C, to A ⊂ C, jeśli A ⊂ B i B ⊂ A, to A = B. Wnioskujemy stąd, że rodzina A jest uporządkowana przez relację inkluzji.
Każdy niepusty podzbiór X zbioru ℜ wszystkich liczb rzeczywistych jest uporządkowany przez relację ≤ (niewiększości). Dla dowolnych liczb rzeczywistych x, y, z należących do X spełnione są bowiem następujące warunki:
x ≤ x, (x ≤ y ∧ y ≤ z) → x ≤ z, (x ≤ y ∧ y ≤ z) → x = y.
Jeżeli zbiór X jest skończony to dowolną relację ≤ porządkującą ten zbiór można opisać podając ilustrację geometryczną za pomocą tak zwanych diagramów. Wyjaśnimy to na kilku przykładach.
Rysunki 5 - 9 przedstawiają diagramy relacji porządkujących pewne zbiory skończone.
![]()
Rysunek 5 przedstawia diagram relacji ≤ porządkującej zbiór X = {a, b}. Jest to relacja zwrotna, a więc a ≤ a i b ≤ b, a ponadto a ≤ b, bo punkty a i b są połączone odcinkiem i a znajduje się poniżej punktu b. Łatwo sprawdzamy, że opisana relacja jest przechodnia i antysymetryczna.
Badamy przechodniość. Mamy tylko dwa elementy a i b, więc (a ≤ b) ∧ (b ≤ b) → (a ≤ b), element b pełni tu rolę elementu trzeciego.
Antysymetria. Implikację (x R y ∧ y R x) → (x = y) można zapisać, jako wyrażenie:
~ (x R y) ∨ ~ (y R x) ∨ (x = y).
Dla x = y = a trzeci człon alternatywy jest prawdziwy, dla x = y = b - również, a dla a ≠ b zachodzi a ≤ b, czyli drugi człon alternatywy jest prawdziwy. Tak więc zbiór A = {a, b} jest uporządkowany. Ponadto ponieważ a ≠ b, to zachodzi prawdziwa alternatywa (a ≤ b lub b ≤ a) relacji spójnej. Relacja ≤ jest równocześnie asymetryczna, bo skoro a ≤ b, to ~ (b ≤ a) dla a ≠ b.
W podobny sposób możemy wykazać uporządkowanie elementów rysunków 6 - 9. Zauważmy jednak, że żaden z nich nie spełnia relacji spójności.
Relacje liniowo porządkujące zbiory
Relację R ⊂ X ![]()
X nazywamy liniowo porządkującą zbiór X, jeśli jest ona równocześnie asymetryczna, przechodnia i spójna.
Przykłady:
Relacja < (mniejszości w zbiorze liczb rzeczywistych) lub relacja większości (>) w tym zbiorze jest relacją, która ten zbiór porządkuje liniowo.
Niech X = {a1, a2, a3} i mamy zbiór par uporządkowanych utworzonych z tych elementów postaci
R = {<a1, a3〉, <a2, a1〉, <a2, a3〉}.
Relacja R ustala następującą liniową kolejność elementów zbioru A: a2, a1, a3.
Graficznie:
Rys.10. Graficzna ilustracja uporządkowania zbioru {a2, a1, a3}.
Innym przykładem relacji porządkującej zbiór (częściowo) jest relacja, która jest równocześnie asymetryczna i przechodnia. Jest to więc również relacja wyrażająca pewien stosunek poprzedzania, zachodzący między elementami. Na przykład relacja starszeństwa w zbiorze ludzi nie ustala żadnej kolejności wśród rówieśników. Niech a1 i a2 są rówieśnikami, a a3 jest od nich starszy, od a3 starszy jest a4 od a4 starszy jest a5 i starszy jest a6, lecz a5 i a6 są rówieśnikami. Mamy więc ustalony następujący częściowy porządek zbioru:
X = {a1, a2, a3, a4, a5, a6}
przez
R = {<a1, a3〉, <a2, a3〉, <a3, a4〉, <a4, a5〉, <a4, a6〉}
Graficznie porządek ten przedstawia rysunek 9.
Podsumowanie
Podstawowym celem autora było przybliżenie podstawowych pojęć logiki klasycznej studentom studiującym kierunki związane z zarządzaniem, gdzie na każdym kroku spotykamy się z potrzebą podjęcia jakiejś decyzji. Logika potrafi pokazywać na podstawie jakich przesłanek została podjęta jakaś decyzja. Autor ma również nadzieję, że ten elementarnie wyłożony wykład przybliżył studentom zrozumienie logiczniej struktury schematów logicznego wnioskowania. Ponadto mam nadzieję, że studenci zrozumieli poprzez ten wykład, iż nie należy wnioskować na podstawie sprzecznych przesłanek.
Literatura
A. Grzegorczyk, Zarys logiki matematycznej. (Wydanie drugie). PWN, Warszawa, 1969.
L. Borkowski, Logika formalna. (Wydanie drugie). PWN, Warszawa, 1977.
H. Rasiowa, Wstęp do matematyki współczesnej. (Wydanie drugie). PWN, Warszawa, 1969.
B. Stanosz, Wprowadzenie do logiki formalnej. Podręczniki dla humanistów. Wydawnictwo Naukowe PWN, Warszawa, 2005.
J. Słupecki, K. Hałkowska, K. Piróg - Rzepecka, Logika i teoria mnogości. (Wydanie drugie). Wydawnictwo naukowe PWN, Warszawa, 1994.
Literatura uzupełniająca
K. Ajdukiewicz, Logika pragmatyczna. PWN, Warszawa, 1965.
J. Cichoń, Wykłady ze wstępu do matematyki. Dolnośląskie Wydawnictwo Edukacyjne, Wrocław, 2003.
Ż. Moszner, O teorii relacji. PZWS, Warszawa, 1967.
18
Wyszukiwarka