1. Liczba podręczników zakupionych na początku roku akademickiego przez studentów w grupie liczącej 20 osób była następująca:

3, 2, 3, 0, 4, 6, 4, 6, 1, 5, 0, 3, 5, 4, 0, 3, 4, 5, 4, 2.

Określ zbiorowość, jednostkę zbiorowości, liczność próby, badaną cechę zmienną. Przedstaw powyższe dane w postaci szeregu rozdzielczego, a następnie przedstaw rozkład graficznie.

2. Liczba nie wykorzystanych pokoi w pewnym hotelu sieci Astor w kolejnych dniach kwietnia była następująca:

13, 38, 7, 10, ,14, 26, 19, 8, 11, 5, 12, 20, 25, 44, 10, 0, 26, 18, 5, 22, 16, 4, 7, 17, 28, 33, 7, 11, 8, 14

Określ badaną zbiorowość statystyczna, jej element, podaj liczność próby oraz określ badaną cechę zmienną. Przedstaw zebrany materiał statystyczny w postaci szeregu rozdzielczego. Przedstaw histogram oraz wielobok liczebności tego rozkładu.

3. Rozkład liczby błędów drukarskich na 50 stronach składu był następujący:

Liczba błędów	0	1	2	3	5
Liczba stron	15	18	12	4	1

Określ badaną zbiorowość i jej element statystyczny. Podaj badaną cechę zmienną. Określ formę przedstawienia materiału statystycznego. Utwórz skumulowany szereg rozdzielczy i zaprezentuj go graficznie. Podaj wzór dystrybuanty empirycznej rozkładu i sporządź jej wykres.

4. Wśród kupujących samochody przeprowadzono ankietę na temat pewnego nowego rozwiązania technicznego. Zbadano ogółem 50 osób, spośród których 22 opowiedziały się za wprowadzeniem nowego rozwiązania, 15 było przeciwnych, a pozostali nie mieli zdania. Przedstaw zebrany materiał statystyczny w postaci szeregu rozdzielczego, a także graficznie histogramem i wykresem kołowym. Czy można określić dystrybuantę tej cechy?

5. Waga (w kg) 20 poborowych, którzy stanęli w pewnym dniu przed komisją poborową była następująca:

76, 67, 80, 73, 69, 73, 64, 85, 77, 74, 76, 76, 58, 63, 74, 69, 81, 74, 71, 83.

Utwórz szereg rozdzielczy przedziałowy o jednakowej rozpiętości klas równej 5 kg i dolnej granicy pierwszego przedziału równej 55 kg. Przedstaw histogram i wielobok liczebności. Utwórz skumulowany szereg rozdzielczy i przedstaw go w postaci wieloboku liczebności skumulowanych. Sporządź wykres dystrybuanty empirycznej dla szeregu rozdzielczego punktowego oraz dla szeregu rozdzielczego przedziałowego.

6. Stopa bezrobocia rejestrowanego w procentach w Polsce według województw na dzień 31.12.1996. kształtowała się następująco:

4,1; 11,9; 11, 7; 9,6; 16,7; 13,1; 19,0; 12,1; 23,4; 10,6; 17,0; 18,2; 14,9; 8,4; 15,2; 17,3; 24,7; 6,1; 14,9; 16,9; 12,0; 11,7; 14,3; 16,2; 12,8; 23,6; 12,9; 17,0; 17,4; 16,8; 16,6; 6,2; 14,2; 17,2; 14,6; 10,7; 12,7; 10,7; 25,7; 24,6; 13,1; 13,9; 12,4; 18,6; 21,7; 21,5; 9,8; 12,4; 15,3.

Scharakteryzuj badaną zbiorowość statystyczną, jednostkę i cechę zmienną. Utwórz szereg rozdzielczy i zaprezentuj go graficznie.

7. Strukturę rodzin według liczby członków rodziny w miejscowości L charakteryzuje poniższy rozkład:

liczba członków rodziny	2	3	4	5	6	7	8
odsetek rodzin	15	30	20	15	10	5	5

Podaj wzór dystrybuanty empirycznej rozkładu liczby członków rodziny w miejscowości L i sporządź jej wykres. Przeprowadź analizę kompleksową liczby członków rodziny w miejscowości L i zinterpretuj uzyskane wyniki.

8. W jednym z domów akademickich przeprowadzono badanie dotyczące miesięcznych wydatków na cele kulturalne. Otrzymano następujące wyniki:

odsetek studentów	10	30	40	20
wydatki miesięczne w złotówkach	40 - 80	80 - 120	120 - 160	160 - 200

Przeprowadź analizę kompleksową miesięcznych wydatków na cele kulturalne. Zinterpretuj uzyskane wyniki.

9. Dzienne zużycie energii elektrycznej (w kWh) w pewnym budynku mieszkalnym kształtowało się następująco:

zużycie	2 - 4	4 - 6	6 - 8	8 - 10	10 - 12	12 - 14
odsetek rodzin	6	10	30	40	10	4

Oblicz miary tendencji centralnej oraz współczynnik zmienności. Wyznacz typowy obszar zmienności.

10. Rozkład szkół podstawowych pod względem liczby uczniów przedstawia się następująco:

liczba uczniów w szkole	0 - 40	40 - 80	80 - 120	120 - 160	160 - 200
liczba szkół	10	60	70	65	100

Zadaj siłę koncentracji.

11. Gra polega na wylosowaniu 2 kart z talii 24. Jeśli są to 2 asy zarabia się 10 punktów, jeśli inne figury zarabia się 5 punktów. W pozostałych przypadkach traci się 2 punkty. Niech zmienna losowa X oznacza wygraną. Wyznaczyć jej rozkład, dystrybuantę oraz parametry rozkładu.

12. Sprawdzamy kolejno jakość 4 przyrządów. Sprawdzanie zostaje przerwane po napotkaniu pierwszego niesprawnego przyrządu. Znaleźć rozkład zmiennej losowej X określającej liczbę sprawdzonych przyrządów, jeśli prawdopodobieństwo, że dowolny przyrząd jest sprawny wynosi 0,9. Podać wzór i wykres dystrybuanty.

13. Na trasie samochodu znajdują się 4 sygnalizacje świetlne, z których każdy z prawdopodobieństwem 0,75 przepuszcza samochód. Wyznaczyć rozkład zmiennej losowej Y równej liczbie sygnalizacji przed pierwszym zatrzymaniem się.

14. Pracownik obsługuje 3 maszyny. Prawdopodobieństwo, że w ciągu jednej godziny maszyna nie będzie wymagać jego interwencji wynosi: 0,6 dla pierwszej maszyny, 0,7 dla drugiej oraz 0,8 dla trzeciej maszyny. Maszyny pracują niezależnie od siebie. Wyznaczyć rozkład i dystrybuantę liczby maszyn, które w ciągu godziny ich pracy nie wymagają interwencji pracownika.

15. Prawdopodobieństwo trafienia do celu jednym strzałem jest równe
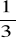
    . Znaleźć rozkład, dystrybuantę i parametry rozkładu zmiennej losowej Z równej liczbie celnych strzałów w wykonanej serii 4 niezależnych strzałów. Obliczyć prawdopodobieństwo, że liczba strzałów celnych jest nie mniejsza niż 2.

16. Sprawdzamy jakość wyrobów. Prawdopodobieństwo, że wynik sprawdzianu dla dowolnego wyrobu będzie pozytywny jest równe 0,8. Sprawdzanie przerywamy po napotkaniu pierwszego wadliwego wyrobu. Wyznaczyć rozkład, dystrybuantę i parametry.

17. Zmienną losową określa funkcja gęstości:

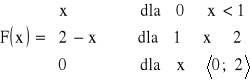
Naszkicuj wykres funkcji gęstości, a następnie podaj wzór i wykres dystrybuanty.

18. Naszkicuj na wspólnym układzie współrzędnych wykresy funkcji gęstości rozkładów:

(a) N(2; 2); N(2; 4); N(2; 0,5)

(b) N(2; 2); N(4; 2); N(0,5; 2)

19. Zmienna losowa X ma rozkład normalny N(1; 2). Oblicz następujące prawdopodobieństwa:

;
;
;
;

20. Pewien automat produkuje części, których długość jest zmienną losową o rozkładzie normalnym N(2; 0,2). Obliczyć prawdopodobieństwo otrzymania dobrej części, jeśli dopuszczalna długość części powinna zawierać się w przedziale
    .

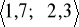
21. Błąd losowy popełniany przy pomiarze czasu dojazdu do pracy pracowników pewnej firmy jest zmienną losową o funkcji gęstości:

Wyznaczyć średni błąd pomiaru i odchylenie standardowe tego błędu. Czy gdyby funkcja gęstości miała postać:

mogłoby to oznaczać pomiar doskonały?

22. Opóźnienie przyjazdu pociągu do stacji A jest zmienną losową o rozkładzie normalnym N(15min; 13min). Obliczyć prawdopodobieństwo, że:

1. pociąg, który miał przyjechać o 22⁰⁰ przyjedzie między 22⁰⁵ a 22¹⁰;

2. ten sam pociąg przyjedzie po 22⁰⁰.

23. Wiek komputerów w pewnej firmie kształtuje się zgodnie z rozkładem normalnym. Ustalić prawdopodobieństwo wylosowania komputera, który ma od 3 do 6 lat, przy założeniu, że:

1. wśród 200 komputerów 100 ma powyżej 5 lat, a
   = 1;

2. prawdopodobieństwo wylosowania komputera, który ma powyżej 6 lat wynosi 0,6, a
   = 4.

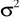
24. Pewna zmienna losowa X ma dystrybuantę określoną wzorem:

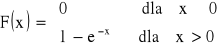
1. wyznacz funkcję gęstości i przedstaw ja graficznie;

2. podaj parametry rozkładu;

3. oblicz
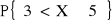
   dwoma sposobami - z funkcji gęstości oraz z dystrybuanty. Zinterpretuj otrzymany wynik graficznie.

25. Wiek komponentów w pewnej firmie kształtuje się zgodnie z rozkładem normalnym. Ustalić prawdopodobieństwo wylosowania komponentu, który ma 3 - 6 lat, przy założeniu, że N(5, 1).

26. Rozkład miesięcznych dochodów na jedną osobę w rodzinach pracowniczych 3-osobowych jest normalny o parametrach N(580,100). Na podstawie tych informacji obliczyć:

1. prawdopodobieństwo, że w losowo wybranej rodzinie będzie dochód powyżej 800 złotych;

2. ile rodzin, spośród 1000 wybranych losowo, będzie miało dochód na 1 osobę poniżej 600 złotych.

27. Zmienna losowa X ma rozkład o gęstości:

.

Wyznaczyć dystrybuantę i prawdopodobieństwo
. Zrobić wykres dystrybuanty i funkcji gęstości. Obliczone prawdopodobieństwo zinterpretować na wykresie dystrybuanty i funkcji gęstości.

28. Robotnik obsługuje trzy maszyny. Prawdopodobieństwo, że w ciągu godziny maszyna nie będzie wymagała jego interwencji dla maszyny pierwszej wynosi 0,6; dla drugiej - 0,7; dla trzeciej - 0,8, przy założeniu, że maszyny pracują niezależnie od siebie. Wyznaczyć rozkład zmiennej losowej, dystrybuantę, parametry rozkładu zmiennej losowej (liczby maszyn, które w ciągu godziny nie wymagają interwencji pracownika).

29. Waga dorosłych pacjentów przychodni rodzinnych w pewnym mieście ma rozkład normalny N(m, 8kg), tzn. z nieznaną średnią wagi i odchyleniem standardowym równym 8 kg. W celu oszacowania średniej wagi pacjentów wylosowano 15 kart pacjentów uzyskując następujące dane (w kg):

76, 82, 67, 52, 79, 86, 77, 70, 68, 76, 80, 74, 66, 60, 63.

Oszacować:

1. punktowo wagę średnią ogółu pacjentów przychodni rodzinnych w tym mieście;

2. przedziałowo wagę średnią ogółu pacjentów przychodni rodzinnych przyjmując współczynnik ufności równy 0,95.

30. W centrali telefonicznej dokonano 17-tu obserwacji długości losowo wybranych rozmów w ciągu dnia i otrzymano w minutach średnią z próby równą 5,48 oraz odchylenie standardowe równe 1,2. Na tej podstawie wyznaczyć przedział ufności średniej długości rozmów w ciągu dnia przy współczynniku ufności równym 0,95, przy założeniu, że długości rozmów mają rozkład normalny.

31. Zainteresowanie budową centrum handlowego pewne przedsiębiorstwo handlowe chce ocenić średnią liczbę samochodów przejeżdżających pobliską drogą w ciągu dnia. Dla losowo wybranych 100 dni otrzymano średnią równą 2150 samochodów oraz odchylenie standardowe 450 samochodów. Na poziomie ufności 0,95 określić przedział ufności dla wartości oczekiwanej.

32. Należy przebadać punkty handlu detalicznego pod względem miesięcznego utargu otrzymanego ze sprzedaży tłuszczów roślinnych. Z próby losowej o liczebności 600 punktów handlu detalicznego otrzymano średnią z próby 45100 PLN oraz odchylenie standardowe 12050 PLN. Wyznaczyć długość przedziału ufności dla średniego utargu w tej grupie produktów w populacji generalnej, przyjmując współczynnik ufności na poziomie 0,99.

33. W celu polepszenia jakości reklam lokalna stacja radiowa chce określić przeciętny wiek swoich słuchaczy. Wybrano losowo 150 słuchaczy i otrzymano średnią wieku 38,6 lat oraz odchylenie standardowe z próby równe 5 lat. Wyznaczyć przedział ufności dla wartości oczekiwanej wieku słuchaczy przy współczynniku ufności równym 0,94. Jaką interpretację praktyczną ma znaleziony przedział?

---