Wykłady z ekonometrii

rok akademicki 2002/2003

Literatura

1. Amir D. Aczel, Statystyka w zarządzaniu. Pełny wykład, PWN, Warszawa 2000

2. Wiesław Dziubdziela, Ekonometria. Materiały pomocnicze, Wydawnictwo WSH, Kielce 2000.

3. Ashish Sen, Muni Srivastava, Regression analysis. Theory, Methods, and Applications, Springer-Verlag, New York 1990.

4. Aleksander Welfe, Ekonometria. Metody i ich zastosowanie, PWE, Warszawa 1998.

1. Wiadomości wstępne.

Ekonometria zajmuje się specyficznymi metodami statystycznymi pozwalającymi badać związki występujące pomiędzy różnorodnymi wielkościami ekonomicznymi.

Cele ekonometrii:

1. Poznawczy - opis związku między interesującymi nas wielkościami, procesami ekonomicznymi. Polega to na konstrukcji modeli ekonometrycznych.

2. Prognoza - wykorzystanie modelu ekonometrycznego do przewidywania dalszego przebiegu interesującego nas procesu ekonomicznego.

3. Symulacja - wykorzystanie modelu ekonometrycznego do przeprowadzenia symulacji przebiegu interesującego nas procesu ekonomicznego. Wyniki można wykorzystywać do regulacji i kontroli procesu.

Przykład modelu ekonometrycznego

Przyjmijmy, ze pewne przedsiębiorstwo wytwarza dobro A jako jedyny producent w kraju. Wysokie cło chroni producenta przed konkurencją artykułów importowanych. Szukamy związku między wielkością y popytu na dobro A, a przeciętnymi realnymi dochodami rocznymi na mieszkańca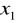
oraz ceną dobra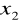
.

Konstrukcja modelu. Przyjmujemy, że funkcja popytu ma postać

,

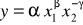
gdzie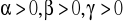
są parametrami modelu. Parametry oszacowuje się na podstawie danych empirycznych (historycznych), czyli obserwacji interesujących nas wielkości w latach poprzednich.

Prognoza. Model można wykorzystać np. do przewidzenia popytu w przypadku, gdy znamy dochód i cenę.

Symulacja. Można podjąć próbę odpowiedzi np. na pytanie: Jaka powinna być produkcja dobra A, aby nie postały jego zapasy? Przeprowadzamy symulację, tzn. wykorzystujemy model do określenia wielkości popytu dla różnych możliwych dochodów i cen.

Uwagi o konstrukcji modeli ekonometrycznych

Naszym celem jest podanie modelu statystycznego związku pomiędzy obserwowanymi wielkościami. Model statystyczny to zbiór matematycznych wzorów i założeń, które opisują pewną sytuację zachodzącą w świecie rzeczywistym. Model powinien możliwie najlepiej pasować do obserwacji, czyli dobrze opisywać procesy generujące obserwacje. We wszystkich realnych sytuacjach występuje pierwiastek niepewności, zatem model nie może wyjaśniać wszystkiego i jest obarczony błędem. Różne zewnętrzne i wewnętrzne na ogół nie znane nam czynniki wpływają na proces generujący obserwacje i wyniki obserwacji są obarczone błędem losowym. Model statystyczny ma na celu wydobycie z wyników obserwacji tego co jest systematyczne, dopuszczając występowanie losowych błędów.

MODEL STATYSTYCZNY

wynik obserwacji = składnik systematyczny + składnik losowy (błąd losowy)

Przykład 1.1 (Wzrost i waga). Interesuje nas związek między wagą y (w kg) a wzrostem x (w cm) mężczyzny. Przyjmujemy, że

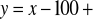
składnik losowy.

Jeżeli w modelu nie byłoby składnika losowego, to wynikałoby z niego, że wszyscy mężczyźni o danym wzroście powinni jednakowo ważyć.

Kolejne kroki budowy modelu statystycznego

1. Ustalenie założeń i postaci modelu.

2. Oszacowanie parametrów modelu na podstawie wyników obserwacji.

3. Zbadanie poprawności modelu. Jeżeli model poprawny, to 4), w przeciwnym przypadku wracamy do 1).

4. Wykorzystanie modelu.

1

2