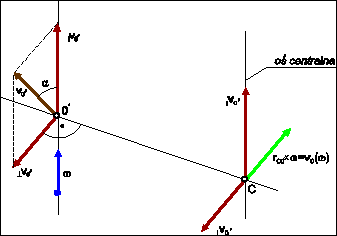
[37] Interpretacja geometryczna procedury prowadzącej do wyznaczenia położenia punktu C (osi centralnej)

Wektor ω i v_0' wyznaczają pewną płaszczyznę. Wektor v_0'≡M_0' rozkładamy na składową _||M_0' i _⊥M_0' i prowadzimy prostą prostopadłą do wspomnianej płaszczyzny i przechodzącą przez punkt 0^/.

Poszukiwany punkt C będzie leżał na tej prostej po jednej ze stron wspomnianej płaszczyzny.

Wybierzmy go w taki sposób, aby

(6.142)

Oznacza to, że

czyli jak widać z rys. 6.20 momenty
. Oznacza to, że w punkcie C wektory
leżą na jednej prostej, mają zwroty przeciwne i jednakowe długości, czyli znoszą się wzajemnie.

Ostatecznie wektor momentu liczonego względem punktu C jest równoległy do wektora ω, bo
. Z kolei długość wektora r_C0 dobieramy z warunku, aby

(6.143)

Zmiany składowych normalnych punktów 0^/ i A przy zbliżaniu się do punktu C przedstawiono na rys. 6.21