ĆWICZENIE NR 1 Wyznaczanie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego.
Zagadnienia teoretyczne:
- Prawo powszechnej grawitacji, ciężar ciała, przyspieszenie ziemskie
- Ruch drgający: drgania harmoniczne proste na przykładzie wahadła matematycznego i wahadła fizycznego, okres drgań (wyprowadzenie), długość zredukowana wahadła fizycznego
- Wahadło rewersyjne, metoda wyznaczania przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
Teoria:
Newtonowskie prawo powszechnego ciążenia stwierdza, że wszystkie ciała oddziaływują ze sobą wzajemnie siłą przyciągającą skierowaną wzdłuż prostej łączącej środki mas obu ciał i mającą wartość:
![]()
gdzie: M1, M2 - masy oddziaływujących ciał R - odległość między środkami mas γ - stała grawitacyjna ( γ = 6,67 ⋅ 10-11 N⋅m2 / kg2 )
Zgodnie z tym prawem ciała znajdujące się w polu grawitacyjnym Ziemi podlegają działaniu grawitacyjnej siły przyciągania. Z uwagi na to, że Ziemia jest układem nie inercjalnym, na ciało spoczywające na powierzchni Ziemi obok siły przyciągania grawitacyjnego działają siły: odśrodkowa i Coriolisa. Ciało naciska na Ziemię z siłą równą wypadkowej trzech sił zwanej ciężarem. Ciężar to siła, która nadaje ciałom przyspieszenie ziemskie: Q = mg
gdzie: Q - ciężar ciała
m - masa ciała
g - wektor przyspieszenie ziemskiego (g = 9,80665 m/s2)
Ruch drgający harmoniczny to ruch, w którym następuje okresowa zmienność określonej wielkości fizycznej np. przyspieszenia x. Układ wykonuje drgania harmoniczne, jeżeli działa na niego siła zwracająca tzn. siła skierowana zawsze w stronę położenia równowagi o wartości proporcjonalnej do wartości wychylenia x z położenia równowagi: F = -kx
gdzie: k - współczynnik proporcjonalności
![]()
wzór na okres drgań:
Wahadło matematyczne jest to wyidealizowane ciało o punktowej masie
zawieszonej na cienkiej, nierozciągalnej i nieważkiej nici. Okres drgań wahadła można przedstawić wzorem:
gdzie: l - długość wahadła matematycznego
![]()
4. Wahadło fizyczne jest to dowolne ciało sztywne mogące obracać się wokół
poziomej osi, nieprzechodzący przez środek jego masy. Okres drgań dla wahadła fizycznego dla małych wychyleń można obliczyć ze wzoru:
gdzie: m - masa wahadła fizycznego
![]()
I - moment bezwładności d - odległość między środkiem ciężkości, a punktem przez który przechodzi oś obrotu.
lub gdzie: l2r - długość redukowana wahadła fizycznego (jest długością
takiego wahadła matematycznego, którego okres drgań jest identyczny jak okres drgań danego wahadła fizycznego).
![]()
5. Wahadło rewersyjne jest to wahadło fizyczne, którego konstrukcja umożliwia
precyzyjny pomiar długości zredukowanej.
Kolejność wykonania ćwiczenia:
1.Wyznaczamy odległość między ostrzami | O1O2| = l2r
2.Wieszamy wahadło na ostrzu O1 i ustawiamy masę m2 w punkcie A
![]()
3.Przesuwamy masę m2 od punktu A do B co 5cm wyznaczając dla kolejnych jej położeń li okresy wahań wahadła Ti (w tym celu mierzymy czas ti, np. h = 10 wahnięć i obliczamy czas jednego wahnięcia ze wzoru:
Wyniki umieszczamy w tabelce.
4.Wieszamy wahadło na ostrzu O2 i przesuwając masę m2 od punktu B do A
powtarzamy czynność z punktu 3.:
Lp. |
l2r |
li |
Tli |
T2i |
T |
g ± Δg |
- |
[ ] |
[ ] |
[ ] |
[ ] |
[ ] |
[ ] |
1. |
|
|
|
|
|
|
2. |
|
|
|
|
|
|
25. |
|
|
|
|
|
|
Przykładowe obliczenia:
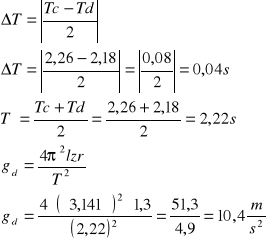
Tc = 2,26s Td = 2,18s
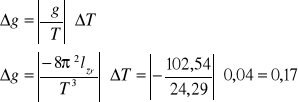
Wnioski:
Wyniki naszego doświadczenia zależały głównie od dokładności reakcji mierzącego czas pięciu pełnych wychyleń wahadła od położenia równowagi.
Także wielkość tego wychylenia miała istotny wpływ na dokładność naszych pomiarów. Im wychylenie to było mniejsze, tym wyniki naszych pomiarów były dokładniejsze.
![]()
![]()
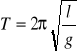
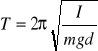
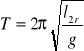
![]()
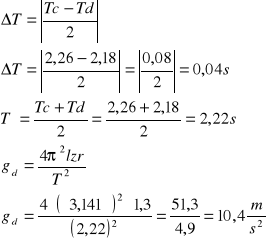
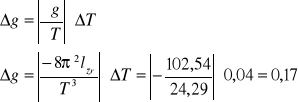
Wyszukiwarka