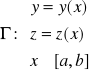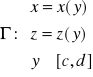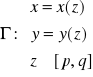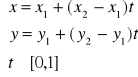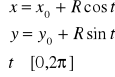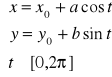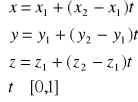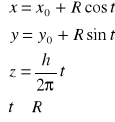1. CAŁKI KRZYWOLINIOWE NIEZORIENTOWANE
1.1 ŁUKI NA PŁASZCZYŹNIE I W PRZESTRZENI
Def. 1.1.1 (funkcja wektorowa jednej zmiennej)
Funkcją wektorową jednej zmiennej nazywamy odwzorowanie
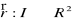
lub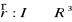
, gdzie I oznacza przedział na prostej. Funkcje wektorowe będziemy zapisywali odpowiednio w postaci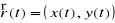
lub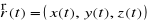
, gdzie t ∈ I.Mówimy, że funkcja wektorowa
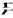
jest różnowartościowa na przedziale I, gdy dla dowolnych t1, t2 ∈ I prawdziwa jest implikacjaJeżeli funkcje x, y lub x, y, z są ciągłe na przedziale I, to mówimy, że funkcja wektorowa
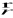
jest ciągła na I.Podobnie, jeżeli funkcje x, y lub x, y, z są różniczkowalne w sposób ciągły na I, to mówimy, że funkcja wektorowa
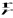
jest różniczkowalna w sposób ciągły na I. Pochodną funkcji wektorowej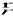
określamy wzorem:Niech funkcja
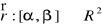
będzie ciągła i różnowartościowa na przedziale [α,β]. Łukiem zwykłym na płaszczyźnie nazywamy zbiór:Niech funkcja
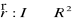
, gdzie I oznacza dowolny odcinek, półprostą lub prostą (z końcem lub nie), będzie ciągła i lokalnie różnowartościowa na I. Łukiem na płaszczyźnie nazywamy zbiór:Jeżeli dla łuku

spełniona jest równość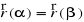
, to mówimy, że łuk ten jest zamknięty. W przeciwnym przypadku mówimy, że łuk Γ jest niezamknięty.Jeżeli funkcja
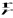
w definicji łuku zwykłego jest różniczkowalna w sposób ciągły na [α,β] oraz dla każdego t ∈ [α,β] spełniony jest warunek:Γ: y = y(x), a ≤ x ≤ b,
Γ: x = x(y), c ≤ y ≤ d.
Odcinek AB o końcach A = (x1,y1), B = (x2,y2) ma przedstawienie parametryczne:
Okrąg o środku w punkcie S = (x0,y0) i promieniu R > 0 ma przedstawienie parametryczne:
Elipsa o środku w punkcie S = (x0,y0) i półosiach a > 0, b > 0 ma przedstawienie parametryczne:
Odcinek AB o końcach A = (x1,y1,z1), B = (x2,y2 ,z2) ma przedstawienie parametryczne:
Linia śrubowa o skoku h > 0, nawinięta na walec (x - x0)2 + (y - y0)2 = R2, gdzie R > 0, ma przedstawienie parametryczne:
istnieje całka krzywoliniowa niezorientowana z funkcji f + g po łuku Γ oraz
istnieje całka krzywoliniowa niezorientowana z funkcji cf po łuku Γ oraz
Jeżeli
Podobnie, jeżeli
Długość łuku Γ na płaszczyźnie lub w przestrzeni wyraża się wzorem:
Niech Σ oznacza powierzchnię boczną walca o tworzących przechodzących przez łuk Γ ⊂ R2. Tworzące walca są równoległe do osi Oz i w punkcie (x,y) ∈ Γ mają długość f(x,y) ≥ 0. Wtedy pole powierzchni Σ wyraża się wzorem:
Masa łuku materialnego Γ ⊂ R2 o gęstości liniowej masy λ wyraża się wzorem:
Momenty statyczne względem osi układu łuku materialnego Γ ⊂ R2 o gęstości liniowej masy λ wyrażają się wzorami:
Współrzędne środka masy łuku materialnego Γ ⊂ R2 o gęstości liniowej masy λ wyrażają się wzorami:
Masa łuku materialnego Γ ⊂ R3 o gęstości liniowej masy λ wyraża się wzorem:
Momenty statyczne względem płaszczyzn układu współrzędnych łuku materialnego Γ ⊂ R3 o gęstości liniowej masy λ wyrażają się wzorami:
Współrzędne środka masy łuku materialnego Γ ⊂ R3 o gęstości liniowej masy λ wyrażają się wzorami:
Momenty bezwładności względem osi lub początku układu współrzędnych łuku materialnego Γ ⊂ R3 o gęstości liniowej masy λ wyrażają się wzorami:
Natężenie pola elektrycznego indukowane w punkcie
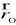
przez ładunek elektryczny o gęstości liniowej ładunku λ rozłożony na łuku Γ ⊂ R2 (R3) wyraża się wzorem:Siła przyciągania grawitacyjnego masy m skupionej w punkcie
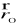
przez łuk materialny Γ ⊂ R2 (R3) o gęstości liniowej masy λ wyraża się wzorem:Energia kinetyczna łuku materialnego Γ ⊂ R3 o gęstości liniowej masy λ, podczas obrotu wokół osi Oy z prędkością kątową ω, wyraża się wzorem:
Jeżeli łuk materialny ma środek symetrii i gęstość liniowa masy jest funkcją symetryczną względem tego środka (np. jest stała), to środek masy łuk pokrywa się z jego środkiem symetrii.
Jeżeli łuk materialny ma oś lub płaszczyznę symetrii i gęstość liniowa masy jest funkcją symetryczną odpowiednio względem tej osi lub płaszczyzny (np. jest stała), to środek masy łuku leży na tej osi lub na płaszczyźnie symetrii.
Niech D będzie obszarem na płaszczyźnie. Polem wektorowym na D nazywamy funkcję wektorową
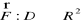
, gdzieNiech V będzie obszarem w przestrzeni. Polem wektorowym na V nazywamy funkcję wektorową
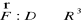
, gdzieJeżeli funkcje P, Q lub P, Q, R są ciągłe odpowiednio na obszarach D lub V, to mówimy, że pole wektorowe
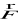
jest ciągłe na tych obszarach.Podobnie, jeżeli funkcje P, Q lub P, Q, R mają ciągłe wszystkie pochodne cząstkowe pierwszego rzędu odpowiednio na obszarach D lub V, to mówimy, że pole wektorowe
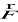
jest różniczkowalne w sposób ciągły na tych obszarach.istnieje całka krzywoliniowa z pola wektorowego
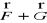
po łuku Γ orazistnieje całka z pola wektorowego
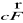
po łuku Γ orazistnieje całka krzywoliniowa z pola wektorowego
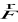
po łuku o orientacji przeciwnej - Γ orazJeżeli
Podobnie, jeżeli
Niech
Podobnie, niech
Niech
Niech
Praca w polu wektorowym
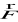
wykonana wzdłuż łuku zorientowanego Γ, od punktu początkowego do końcowego, wyraża się wzorem:Ilość płaskiej (umownej) cieczy przepływającej w jednostce czasu przez łuk zorientowany Γ wyraża się wzorem:
Niech D będzie obszarem na płaszczyźnie. Funkcją wektorową dwóch zmiennych w przestrzeni nazywamy odwzorowanie
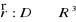
. Funkcję taką będziemy zapisywać w postaciMówimy, że funkcja wektorowa
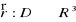
jest różnowartościowa, gdy dla dowolnych punktów (u1,v1), (u2,v2) ∈ D prawdziwa jest implikacjaMówimy, że funkcja wektorowa
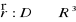
jest ciągła, gdy funkcje x, y, z są ciągłe na D.Mówimy, że funkcja wektorowa
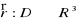
jest różniczkowalna w sposób ciągły, gdy funkcje x, y, z mają ciągłe wszystkie pochodne cząstkowe pierwszego rzędu na obszarze D.Płaszczyzna przechodząca przez punkt
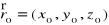
i rozpięta na wektorach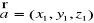
,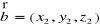
ma przedstawienie parametryczne:Sfera o środku w początku układu współrzędnych i promieniu r > 0 ma przedstawienie parametryczne:
Powierzchnia stożka określona równaniem
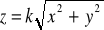
, gdzie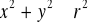
, ma przedstawienie parametryczne:Powierzchnia paraboloidy obrotowej określona równaniem
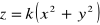
, gdzie
, ma przedstawienie parametryczne:Powierzchnia walcowa opisana równaniem
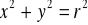
, gdzie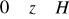
, ma przedstawienie parametryczne: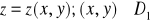
, gdzie D1 jest obszarem na płaszczyźnie xOy,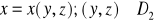
, gdzie D2 jest obszarem na płaszczyźnie yOz,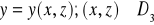
, gdzie D3 jest obszarem na płaszczyźnie xOz.funkcja f + g jest całkowalna na płacie Σ oraz
funkcja cf jest całkowalna na płacie Σ oraz
Masa płata materialnego Σ o gęstości powierzchniowej masy σ wyraża się wzorem:
Momenty statyczne względem płaszczyzn układu współrzędnych płata materialnego Σ o gęstości powierzchniowej masy σ wyrażają się wzorami:
Współrzędne środka masy płata Σ o gęstości powierzchniowej masy σ wyrażają się wzorami:
Momenty bezwładności względem osi oraz względem początku układu współrzędnych płata materialnego Σ o gęstości powierzchniowej masy σ wyrażają się wzorami:
Natężenie pola elektrycznego w punkcie
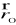
pochodzące od ładunku elektrycznego rozłożonego na płacie Σ o gęstości powierzchniowej ładunku σ wyraża się wzorem:Siła przyciągania grawitacyjnego masy m skupionej w punkcie
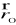
przez płat materialny Σ o gęstości powierzchniowej masy σ wyraża się wzorem:Jeżeli płat powierzchniowy ma środek symetrii i gęstość powierzchniowa masy jest funkcją symetryczną względem tego środka (np. jest stała), to środek masy płata pokrywa się z jego środkiem symetrii.
Jeżeli płat powierzchniowy ma oś lub płaszczyznę symetrii i gęstość powierzchniowa masy jest funkcją symetryczną względem tej osi lub płaszczyzny (np. jest stała), to środek masy tego płata leży na jego osi lub płaszczyźnie symetrii.
istnieje całka z pola wektorowego
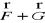
po płacie Σ orazistnieje całka z pola wektorowego
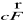
po płacie Σ orazistnieje całka z pola wektorowego
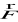
po płacie o orientacji przeciwnej - Σ oraz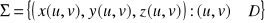
jest gładkim płatem zorientowanym, gdzie D jest obszarem regularnym na płaszczyźnie,pole wektorowe
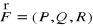
jest ciągłe na płacie Σ,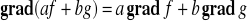
,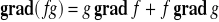
,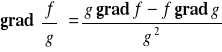
,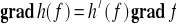
, gdzie h jest funkcją różniczkowalną na pewnym przedziale,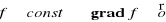
,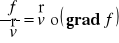
, gdzie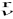
jest wersorem.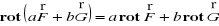
, gdzie a, b ∈ R,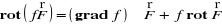
,
, gdzie U jest funkcją dwukrotnie różniczkowalną w sposób ciągły na V.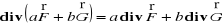
, gdzie a, b ∈ R,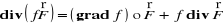
,
,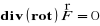
, gdzie pole wektorowe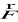
ma współrzędne dwukrotnie różniczkowalne w sposób ciągły na V.Σ jest zorientowanym kawałkami gładkim płatem zamkniętym, który jest brzegiem obszaru domkniętego V ⊂ R3,
pole wektorowe
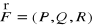
jest różniczkowalne w sposób ciągły na V,Σ jest płatem kawałkami gładkim zorientowanym, którego brzeg Γ jest łukiem kawałkami gładkim zorientowanym zgodnie z orientacją płata Σ,
pole wektorowe
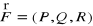
jest różniczkowalne w sposób ciągły na płacie Σ (łącznie z brzegiem Γ),Ilość cieczy przepływającej w jednostce czasu przez płat zorientowany Σ (ze strony ujemnej na dodatnią) wyraża się wzorem:
Parcie cieczy o ciężarze właściwym C na dodatnią stronę płata zorientowanego Σ, który jest zanurzony w tej cieczy, wyraża się wzorem:
|
Rys. 1.1.1 Funkcja wektorowa jednej zmiennej na płaszczyźnie |
![]()
.
Funkcja ![]()
jest lokalnie różnowartościowa na przedziale I, jeżeli każdy punkt tego przedziału ma otoczenie, na którym funkcja ![]()
jest różnowartościowa.
|
Rys. 1.1.2 Funkcja wektorowa jednej zmiennej w przestrzeni |
![]()
lub ![]()
.
|
Rys. 1.1.3 Pochodna funkcji wektorowej |
Def. 1.1.2 (łuki na płaszczyźnie)
![]()
.
|
Rys. 1.1.4 Łuk zwykły na płaszczyźnie |
![]()
.
|
Rys. 1.1.5 Łuk na płaszczyźnie |
|
Rys. 1.1.6 Łuk zamknięty na płaszczyźnie |
![]()
,
to mówimy, że łuk ten jest gładki. Mówimy, że łuk jest kawałkami gładki, jeżeli można go podzielić na skończoną liczbę łuków gładkich.
|
Rys. 1.1.7 Łuk kawałkami gładki na płaszczyźnie |
Uwaga. Podobnie definiuje się łuki analogicznych rodzajów w przestrzeni. Funkcję wektorową ![]()
lub funkcje x, y, z opisujące łuk Γ nazywamy jego parametryzacją. Obrazowo łuk zwykły można przedstawić jako powyginany odcinek ma płaszczyźnie lub w przestrzeni. Wyginany odcinek można wydłużać lub skracać, ale nie wolno go rozrywać ani sklejać.
Fakt 1.1.3 (o przedstawianiu łuków na płaszczyźnie i w przestrzeni)
Łukami na płaszczyźnie są wykresy funkcji ciągłych postaci:
Łukami w przestrzeni są części wspólne ciągłych powierzchni walcowych:
3. |
4. |
5. |
Jeżeli funkcje x, y, z mają ciągłe pierwsze pochodne, to łuki Γ są gładkie.
|
|
|
||
Rys. 1.1.8 Łuk Γ jest wykresem funkcji y = y(x), gdzie x ∈ [a,b] |
|
Rys. 1.1.9 Łuk Γ jest wspólną częścią powierzchni walcowych y = y(x) oraz z = z(x), gdzie x ∈ [a,b] |
||
Fakt 1.1.4 (parametryzacje ważniejszych łuków na płaszczyźnie i w przestrzeni)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jeden zwój linii śrubowej otrzymamy, gdy t ∈ [0,2π].
Uwaga. Równania fragmentów łuków określonych wyżej otrzymamy zmniejszając odpowiednio zakres zmienności parametru t. Na rysunkach strzałką zaznaczono kierunek przebiegu łuków przy wzroście parametru t.
Def. 1.1.5 (długość łuku)
Długością łuku nazywamy kres górny długości łamanych wpisanych w ten łuk;
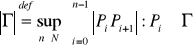
.
|
Rys. 1.1.10 Długość łuku |
Tw. 1.1.6 (długość łuku)
Niech Γ = {(x(t), y(t)) : α ≤ t ≤ β} będzie łukiem gładkim na płaszczyźnie. Wtedy długość tego łuku wyraża się wzorem:
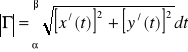
.
Podobnie, niech Γ = {(x(t), y(t), z(t)) : α ≤ t ≤ β} będzie łukiem gładkim w przestrzeni. Wtedy długość tego łuku wyraża się wzorem:
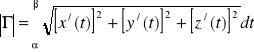
.
Uwaga. Jeżeli łuk Γ jest wykresem funkcji y = y(x), a ≤ x ≤ b, to jego długość wyraża się wzorem:
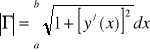
.
1.2 DEFINICJE I WŁASNOŚCI CAŁEK KRZYWOLINIOWYCH NIEZORIENTOWANYCH
Oznaczenia w definicji całki krzywoliniowej niezorientowanej
Niech Γ = {(x(t), y(t)) : t ∈ [α,β]} będzie łukiem gładkim na płaszczyźnie. Wprowadzamy następujące oznaczenia:
P = {t0, t1, ..., tn}, gdzie α = t0 < t1 < … < tn = β - podział odcinka [α,β] na n ∈ N odcinków;
Δtk = tk - tk-1 - długość k-tego odcinka podziału P, 1 ≤ k ≤ n;
δ(P) = max{Δtk: 1 ≤ k ≤ n } - średnica podziału P;
![]()
, gdzie ![]()
dla 1 ≤ k ≤ n - zbiór punktów pośrednich podziału P.
Ak = (x(tk),y(tk)) - punkty podziału łuku Γ indukowane przez podział P, 0 ≤ k ≤ n;
![]()
- punkty pośrednie na łuku Ak-1Ak indukowane przez wybór punktów pośrednich podziału P, 1 ≤ k ≤ n;
Δlk - długość łuku Ak-1Ak ,1 ≤ k ≤ n.
|
|
Rys. 1.2.1 Podział odcinka [α,β] i podział łuku Γ indukowany przez podział tego odcinka |
|
Def. 1.2.1 (całka krzywoliniowa niezorientowana)
Niech f będzie funkcją dwóch zmiennych określoną i ograniczoną na łuku gładkim Γ. Całkę krzywoliniową niezorientowaną z funkcji f po łuku Γ definiujemy wzorem:
![]()
,
o ile granica po prawej stronie znaku równości nie zależy od sposobu podziału P odcinka [α,β], ani od sposobu wyboru punktów pośrednich Ξ.
Uwaga. Wartość całki krzywoliniowej nie zależy od wybranej parametryzacji łuku. Całkę krzywoliniową niezorientowaną z funkcji trzech zmiennych po łuku położonym w przestrzeni definiujemy analogicznie. Całkę krzywoliniową niezorientowaną na płaszczyźnie jak i w przestrzeni oznaczamy krótko symbolem ![]()
.
|
|
Rys. 1.2.2 Ilustracja do definicji całki krzywoliniowej niezorientowanej |
|
Def. 1.2.2 (całka krzywoliniowa po łuku kawałkami gładkim)
Niech Γ będzie łukiem kawałkami gładkim złożonym z łuków gładkich Γ1, Γ2, …, Γm oraz niech f będzie funkcją określoną i ograniczoną na łuku Γ. Całkę krzywoliniową niezorientowaną z funkcji f po łuku Γ definiujemy wzorem:
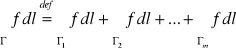
,
o ile całki po prawej stronie znaku równości istnieją.
Tw. 1.2.3 (liniowość całki krzywoliniowej niezorientowanej)
Jeżeli istnieją całki krzywoliniowe niezorientowane z funkcji f i g po kawałkami gładkim łuku Γ i c ∈ R, to:
![]()
,
![]()
.
Def 1.2.4 (całka krzywoliniowa niezorientowana z funkcji wektorowej)
Niech Γ będzie łukiem kawałkami gładkim na płaszczyźnie oraz niech funkcje P i Q będą całkowalne na Γ. Całkę krzywoliniową niezorientowaną po łuku Γ z funkcji wektorowej ![]()
określamy wzorem:

.
Uwaga. Podobnie określa się całkę krzywoliniową niezorientowaną z funkcji wektorowej ![]()
po łuku położonym na płaszczyźnie xOy oraz całkę krzywoliniową niezorientowaną z funkcji wektorowej ![]()
po łuku położonym w przestrzeni.
1.3 ZAMIANA CAŁKI KRZYWOLINIOWEJ NIEZORIENTOWANEJ NA CAŁKĘ POJEDYNCZĄ
Tw. 1.3.1 (o zamianie całki krzywoliniowej niezorientowanej na całkę pojedynczą)
1. łuk Γ = {(x(t), y(t)) : t ∈ [α,β]} jest gładki i niezamknięty,
2. funkcja f jest ciągła na łuku Γ,
to
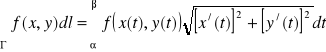
.
1. łuk Γ = {(x(t), y(t), z(t)) : t ∈ [α,β]} jest gładki i niezamknięty,
2. funkcja f jest ciągła na łuku Γ,
to
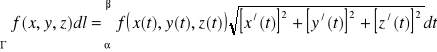
.
Uwaga. W zapisie wektorowym powyższe wzory przyjmują jednolitą postać
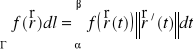
.
Jeżeli funkcja f jest ciągła na łuku gładkim Γ opisanym równaniem y = y(x), gdzie a ≤ x ≤ b, to
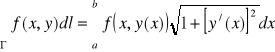
.
1.4 ZASTOSOWANIA CAŁEK KRZYWOLINIOWYCH NIEZORIENTOWANYCH
Fakt 1.4.1 (zastosowania w geometrii)
![]()
.
|
|
|
![]()
.
Fakt 1.4.2 (zastosowania w fizyce)
![]()
.
|
|
|
![]()
, ![]()
.
![]()
, ![]()
.
|
|
|
![]()
.
![]()
, ![]()
, ![]()
.
|
|
|
![]()
, ![]()
, ![]()
.
![]()
,
![]()
,
![]()
,
![]()
.
|
|
|
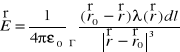
,
gdzie ![]()
, a ε0 oznacza stałą dielektryczną próżni.
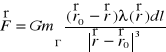
,
gdzie ![]()
, a G oznacza stałą grawitacji.
|
|
|
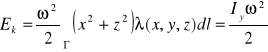
.
Uwaga. Wzór na natężenie pola grawitacyjnego jest analogiczny do wzoru na natężenie pola elektrycznego. Także wzór na siłę przyciągania pochodzącą od ładunków elektrycznych jest analogiczny do wzoru na siłę przyciągania grawitacyjnego.
Fakt 1.4.3 (środki masy łuków symetrycznych)
|
|
|
2. CAŁKI KRZYWOLINIOWE ZORIENTOWANE
2.1 DEFINICJE I WŁASNOŚCI CAŁEK KRZYWOLINIOWYCH ZORIENTOWANYCH
Def. 2.1.1 (pole wektorowe na płaszczyźnie i w przestrzeni)
![]()
dla (x,y) ∈ D.
|
|
|
Rys. 2.1.1 Pole wektorowe na płaszczyźnie |
|
Rys. 2.1.2 Pole wektorowe w przestrzeni |
![]()
dla (x,y,z) ∈ V.
Uwaga. Będziemy także pisali krótko ![]()
, gdzie ![]()
lub ![]()
, gdzie ![]()
.
Def. 2.1.2 (łuk zorientowany)
Łuk zwykły niezamknięty, na którym ustalono początek i koniec (kierunek) nazywamy łukiem zorientowanym. Łuk zorientowany oznaczamy tym samym symbolem co łuk. Łuk o orientacji przeciwnej do orientacji łuku Γ oznaczamy przez - Γ. Jeżeli ze wzrostem parametru łuku zorientowanego poruszamy się po nim w kierunku orientacji, to mówimy, że parametryzacja łuku jest zgodna z jego orientacją.
|
|
|
Rys. 2.1.3 Łuk zorientowany Γ |
|
Rys. 2.1.4 Łuk -Γ o orientacji przeciwnej do łuku zorientowanego Γ |
Oznaczenia w definicji całki krzywoliniowej zorientowanej
Niech Γ będzie łukiem zorientowanym na płaszczyźnie opisanym równaniem parametrycznym ![]()
, gdzie ![]()
oraz ![]()
. Zakładamy przy tym, że orientacja łuku Γ jest zgodna z jego parametryzacją. Wprowadzamy następujące oznaczenia:
P = {t0, t1, ..., tn}, gdzie α = t0 < t1 < … < tn = β - podział odcinka [α,β] na n ∈ N odcinków;
Δtk = tk - tk-1 - długość k-tego odcinka podziału P, 1 ≤ k ≤ n;
δ(P) = max{Δtk: 1 ≤ k ≤ n } - średnica podziału P;
![]()
, gdzie ![]()
dla 1 ≤ k ≤ n - zbiór punktów pośrednich podziału P.
![]()
- punkty podziału łuku Γ indukowane przez podział P, 0 ≤ k ≤ n (A0 jest początkiem, a An końcem łuku zorientowanego Γ);
![]()
- punkty pośrednie na łuku Ak-1Ak indukowane przez wybór punktów pośrednich podziału P, 1 ≤ k ≤ n;
![]()
, gdzie ![]()
, ![]()
, 1 ≤ k ≤ n.
|
|
Rys. 2.1.5 Podział odcinka [α,β] i podział łuku zorientowanego Γ indukowany przez ten podział |
|
Def. 2.1.3 (całka krzywoliniowa zorientowana)
Niech ![]()
będzie polem wektorowym określonym na łuku zorientowanym Γ ⊂ R2. Całkę krzywoliniową zorientowaną z pola wektorowego ![]()
po łuku Γ definiujemy wzorem:
![]()
,
o ile granica po prawej stronie znaku równości istnieje oraz nie zależy od sposobu podziału P przedziału [α,β], ani od sposobu wyboru punktów pośrednich Ξ. Powyższą całkę oznaczamy krótko przez ![]()
.
Uwaga. Całkę krzywoliniową zorientowaną z pola wektorowego ![]()
po łuku Γ położonym w przestrzeni definiujemy analogicznie i oznaczamy symbolem:
![]()
lub krótko ![]()
.
W zapisie wektorowym definicja całki krzywoliniowej zorientowanej z pola wektorowego ![]()
lub pola wektorowego ![]()
po łuku zorientowanym Γ położonym odpowiednio na płaszczyźnie lub w przestrzeni przyjmuje jednolitą formę:
![]()
,
gdzie ![]()
lub ![]()
. Całkę krzywoliniową z pola wektorowego ![]()
po łuku Γ oznaczamy też krótko symbolem ![]()
.
|
|
Rys. 2.1.6 Ilustracja do definicji całki krzywoliniowej zorientowanej w formie wektorowej |
|
Def. 2.1.4 (całka krzywoliniowa po sumie łuków zorientowanych)
Niech łuk zorientowany Γ będzie sumą łuków niezamkniętch zorientowanych Γ1, Γ2, …, Γm, przy czym koniec łuku Γk jest początkiem łuku Γk+1, 1 ≤ k ≤ m - 1. Ponadto niech ![]()
będzie polem wektorowym określonym na łuku Γ. Całkę krzywoliniową zorientowaną z pola ![]()
po łuku Γ określamy wzorem:
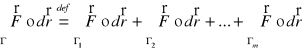
,
o ile całki po prawej stronie znaku równości istnieją.
Uwaga. Jeżeli łuk zorientowany na płaszczyźnie jest zamknięty, to wtedy piszemy ![]()
w miejsce ![]()
.
|
|
Rys. 2.1.7 Ilustracje do definicji całki krzywoliniowej zorientowanej po sumie łuków |
|
Tw. 2.1.5 (liniowość całki krzywoliniowej zorientowanej)
Jeżeli istnieją całki krzywoliniowe z pól wektorowych ![]()
i ![]()
po kawałkami gładkim łuku zorientowanym Γ oraz jeżeli c jest stałą dowolną, to:
![]()
,
![]()
,
![]()
.
Tw. 2.1.6 (zależność między całkami krzywoliniowymi)
Niech pole wektorowe ![]()
będzie ciągłe na łuku gładkim Γ. Wtedy
![]()
,
gdzie α(x,y) oznacza kąt między wektorem stycznym do łuku Γ w punkcie (x,y) a dodatnią częścią osi Ox, natomiast β(x,y) oznacza kąt między tym samym wektorem i dodatnią częścią osi Oy. Zakładamy przy tym, że zwrot wektora stycznego jest zgodny z orientacją łuku Γ.
Uwaga. Prawdziwa jest także analogiczna równość dla całek krzywoliniowych po łuku położonym w przestrzeni. Równości te niektórzy autorzy przyjmują jako definicję całki krzywoliniowej zorientowanej.
|
|
Rys. 2.1.8 Ilustracja do twierdzenia o zależności między dwoma rodzajami całek krzywoliniowych |
|
2.2 ZAMIANA CAŁKI KRZYWOLINIOWEJ ZORIENTOWANEJ NA CAŁKĘ POJEDYNCZĄ
Tw. 2.2.1 (o zamianie całki krzywoliniowej na całkę pojedynczą)
1. łuk Γ = {(x(t), y(t)) : t ∈ [α,β]} jest niezamknięty i gładki,
2. orientacja łuku Γ jest zgodna z jego polaryzacją,
3. pole wektorowe ![]()
jest ciągłe na Γ,
to
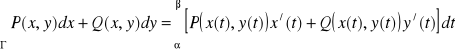
.
1. łuk Γ = {(x(t), y(t), z(t)) : t ∈ [α,β]}jest niezamknięty i gładki,
2. orientacja łuku Γ jest zgodna z jego polaryzacją,
3. pole wektorowe ![]()
jest ciągłe na Γ,
to
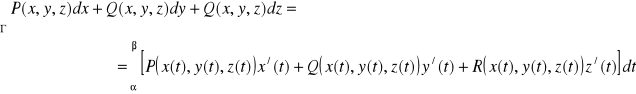
.
Uwaga. Powyższe wzory w formie wektorowej przyjmują jednolitą postać:
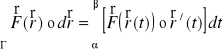
,
gdzie ![]()
jest parametryzacją łuku Γ oraz ![]()
lub ![]()
.
Jeżeli pole wektorowe ![]()
jest ciągłe na łuku gładkim Γ opisanym równaniem y = y(x), gdzie a ≤ x ≤ b i orientacja łuku Γ jest zgodna ze wzrostem zmiennej x, to

.
2.3 NIEZALEŻNOŚĆ CAŁKI OD DROGI CAŁKOWANIA
Def. 2.3.1 (pole potencjalne, potencjał pola)
Pole wektorowe ![]()
określone na obszarze D nazywamy polem potencjalnym, gdy istnieje funkcja U: D → R taka, że
![]()
.
Funkcję U nazywamy potencjałem pola wektorowego ![]()
.
Uwaga. Dla pola wektorowego na płaszczyźnie ![]()
powyższy warunek ma postać
![]()
.
Podobnie, dla pola wektorowego w przestrzeni ![]()
, mamy
![]()
.
Tw. 2.3.2 (całka krzywoliniowa z pola potencjalnego)
1. pole wektorowe ![]()
będzie ciągłe na obszarze D ⊂ R2,
2. pole wektorowe ![]()
będzie potencjalne na obszarze D z potencjałem U.
Wtedy
![]()
,
gdzie ![]()
jest dowolnym zorientowanym kawałkami gładkim łukiem o początku w punkcie A = (x1,y1) i końcu w punkcie B = (x2,y2), całkowicie zawartym w obszarze D.
1. pole wektorowe ![]()
będzie ciągłe na obszarze V ⊂ R3,
2. pole wektorowe ![]()
będzie potencjalne na obszarze V z potencjałem U.
Wtedy
![]()
,
gdzie ![]()
jest dowolnym zorientowanym kawałkami gładkim łukiem o początku w punkcie A = (x1,y1,z1) i końcu w punkcie B = (x1,y1,z1), całkowicie zawartym w obszarze V.
Uwaga. W formie wektorowej powyższe wzory przyjmują jednolitą postać:
![]()
.
Inaczej mówiąc, całka zorientowana w polu potencjalnym nie zależy od drogi całkowania i jest równa różnicy potencjałów w punktach końcowym i początkowym drogi całkowania. W szczególności w polu potencjalnym ![]()
mamy
![]()
,
gdzie Γ jest dowolnym łukiem zamkniętym zawartym w rozważanym obszarze.
Tw. 2.3.3 (warunek konieczny i wystarczający potencjalności pola)
1. obszar D ⊂ R2 będzie wypukły,
2. pole wektorowe ![]()
będzie różniczkowalne w sposób ciągły na D.
Wówczas pole wektorowe ![]()
jest potencjalne na D wtedy i tylko wtedy, gdy
![]()
dla każdego punktu ![]()
.
1. obszar V ⊂ R3 będzie wypukły,
2. pole wektorowe ![]()
będzie różniczkowalne w sposób ciągły na V.
Wówczas pole wektorowe ![]()
jest potencjalne na V wtedy i tylko wtedy, gdy
![]()
, ![]()
, ![]()
dla każdego punktu ![]()
.
Uwaga. Zamiast wypukłości obszarów D i V można założyć, że są one obszarami jednospójnymi odpowiednio na płaszczyźnie lub w przestrzeni.
Def. 2.3.4 (rotacja pola wektorowego)
Niech pole wektorowe ![]()
będzie różniczkowalne w sposób ciągły na obszarze V ⊂ R3. Rotacją pola wektorowego ![]()
nazywamy pole wektorowe określone wzorem:
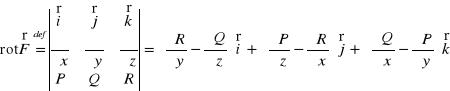
.
Fakt 2.3.5 (kryterium potencjalności pola wektorowego)
Pole wektorowe ![]()
na obszarze V ⊂ R3 jest potencjalne wtedy i tylko wtedy, gdy ![]()
.
2.4 TWIERDZENIE GREENA
Def. 2.4.1 (znak orientacji)
Niech Γ będzie kawałkami gładkim łukiem zamkniętym (bez samoprzecięć) na płaszczyźnie, tzn. krzywą Jordana. Mówimy, że orientacja łuku Γ jest dodatnia względem swego wnętrza D, gdy podczas ruchu łuku Γ w kierunku jego orientacji obszar D leży cały czas po lewej stronie łuku. W przeciwnym przypadku mówimy, że orientacja łuku jest ujemna.
|
|
|
Rys. 2.4.1 Łuk Γ1 jest zorientowany dodatnio względem obszaru D1 |
|
Rys. 2.4.2 Łuk Γ2 jest zorientowany ujemnie względem obszaru D2 |
Tw. 2.4.2 (wzór Greena)
Niech
1. obszar domknięty D ⊂ R2 będzie normalny względem obu osi układu,
2. brzeg Γ obszaru D będzie zorientowany dodatnio,
3. pole wektorowe ![]()
będzie różniczkowalne w sposób ciągły na D.
Wtedy
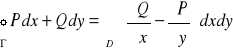
.
Uwaga. Wzór Greena jest prawdziwy także dla obszaru D, który można podzielić na skończoną liczbę obszarów normalnych (względem obu osi).
Def. 2.4.3 (cyrkulacja pola wektorowego)
Cyrkulacją pola wektorowego ![]()
po łuku zamkniętym zorientowanym Γ nazywamy całkę krzywoliniową zorientowaną
![]()
.
2.5 ZASTOSOWANIA CAŁEK KRZYWOLINIOWYCH ZORIENTOWANYCH
Fakt 2.5.1 (zastosowania w geometrii)
Pole obszaru D ⊂ R2 ograniczonego łukiem zamkniętym kawałkami gładkim Γ, dodatnio zorientowanym względem obszaru D, wyraża się wzorami:
![]()
.
|
Fakt 2.5.2 (zastosowania w fizyce)
![]()
.
|
|
|
![]()
,
gdzie ![]()
oznacza prędkość przepływu cieczy w punkcie (x,y) tego łuku.
3. CAŁKI POWIERZCHNIOWE NIEZORIENTOWANE
3.1 PŁATY POWIERZCHNIOWE
Def. 3.1.1 (funkcja wektorowa dwóch zmiennych w przestrzeni)
![]()
, gdzie ![]()
.
|
|
Rys. 3.1.1 Funkcja wektorowa |
|
![]()
.
Def. 3.1.2 (płat powierzchniowy)
Niech D będzie prostokątem na płaszczyźnie oraz niech funkcja wektorowa ![]()
, gdzie ![]()
dla ![]()
, będzie ciągła i różnowartościowa na prostokącie D. Płatem powierzchniowym nazywamy zbiór wartości funkcji wektorowej ![]()
, tj. zbiór:
![]()
.
Zbiór w przestrzeni taki, że każdy jego punkt ma otoczenie domknięte, które jest płatem prostym, nazywamy płatem powierzchniowym.
Uwaga. Funkcję wektorową ![]()
lub układ funkcji x, y, z nazywamy parametryzacją płata Σ. Płat prosty można wyobrazić sobie jako powyginany w przestrzeni prostokąt. Przy tym przekształcaniu prostokąta nie można rozrywać ani sklejać.
|
|
|
Rys. 3.1.2 Zbiór Σ nie jest płatem powierzchniowym |
|
Rys. 3.1.3 Zbiór Σ jest płatem powierzchniowym |
Def. 3.1.3 (płat powierzchniowy gładki)
Płat powierzchniowy ![]()
, gdzie D jest obszarem domkniętym z brzegiem kawałkami gładkim, a funkcja wektorowa ![]()
jest różnowartościowa i różniczkowalna w sposób ciągły na obszarze D, nazywamy płatem gładkim, gdy na obszarze D spełniony jest warunek
![]()
,
gdzie
![]()
oraz ![]()
.
Płat, który można podzielić na skończoną liczbę płatów gładkich, nazywamy płatem kawałkami gładkim.
|
|
|
||
Rys. 3.1.4 Płat powierzchniowy gładki |
|
Rys. 3.1.5 Płat powierzchniowy kawałkami gładki |
||
Fakt 3.1.4 (równania parametryczne ważniejszych płatów powierzchniowych)
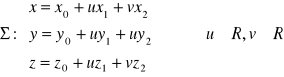
.
W formie wektorowej parametryzacja płaszczyzny ma postać:
![]()
.
|
|
|
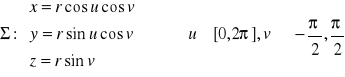
.
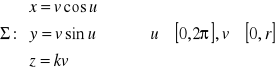
.
|
|
|
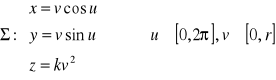
.
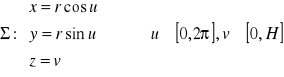
.
Uwaga. Równania fragmentów tych płatów powierzchniowych otrzymamy zmniejszając odpowiednio zakresy parametrów u, v.
Fakt 3.1.5 (o postaci płatów powierzchniowych)
Płatami powierzchniowymi są wykresy funkcji ciągłych postaci:
Jeżeli funkcje te mają ciągłe pochodne cząstkowe pierwszego rzędu na rozważanych obszarach, to te płaty powierzchniowe są gładkie.
Uwaga. Równania ważniejszych płatów powierzchniowych, które są wykresami funkcji postaci z = f(x,y) podane są w części „Analiza matematyczna 2” w fakcie 3.2.5.
Tw. 3.1.6 (pole płata powierzchniowego)
Niech ![]()
będzie gładkim płatem powierzchniowym. Wtedy pole tego płata wyraża się wzorem:
![]()
.
Uwaga. Jeżeli płat gładki Σ jest wykresem funkcji z = z(x,y), gdzie (x,y) ∈ D, to jego pole wyraża się wzorem:
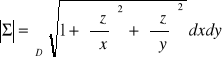
.
Analogicznie wyglądają wzory na pola płatów gładkich będących wykresami funkcji x = x(y,z) oraz y = y(x,z).
3.2 DEFINICJA I WŁASNOŚCI CAŁKI POWIERZCHNIOWEJ NIEZORIENTOWANEJ
Oznaczenia w definicji całki powierzchniowej niezorientowanej
Niech ![]()
będzie gładkim płatem powierzchniowym, zakładamy przy tym, że D jest domkniętym obszarem regularnym na płaszczyźnie. Wprowadzamy następujące oznaczenia:
P = {ΔD1, ΔD2, ..., ΔDn}, - podział obszaru D na obszary regularne ΔDk (o rozłącznych wnętrzach), 1 ≤ k ≤ n;
dk - średnica obszaru ΔDk, tj. kres górny odległości punktów zbioru ΔDk, 1 ≤ k ≤ n;
δ(P) = max{dk: 1 ≤ k ≤ n } - średnica podziału P;
![]()
, gdzie ![]()
dla 1 ≤ k ≤ n - zbiór punktów pośrednich podziału P.
ΔΣk - część płata Σ odpowiadająca obszarowi ΔDk w podanej wyżej parametryzacji ![]()
, 1 ≤ k ≤ n;
|ΔΣk| - pole płata ΔΣk, 1 ≤ k ≤ n;
![]()
- punkt płata ΔΣk odpowiadający punktowi ![]()
w podanej parametryzacji ![]()
, 1 ≤ k ≤ n.
|
|
Rys. 3.2.1 Ilustracja do definicji całki powierzchniowej niezorientowanej |
|
Def. 3.2.1 (całka powierzchniowa niezorientowana)
Niech Σ będzie płatem powierzchniowym gładkim oraz niech funkcja ![]()
będzie ograniczona. Całkę powierzchniową niezorientowaną z funkcji f po płacie Σ definiujemy wzorem:
![]()
,
o ile granica po prawej stronie znaku równości istnieje oraz nie zależy od sposobu podziału P obszaru D, ani od sposobu wyboru punktów pośrednich Ξ.
Uwaga. Wartość całki powierzchniowej niezorientowanej nie zależy od sposobu parametryzacji płata. Całkę powierzchniową niezorientowaną z funkcji f po płacie Σ oznaczamy krótko symbolem ![]()
.
Def. 3.2.2 (całka powierzchniowa po płacie kawałkami gładkim)
Niech Σ będzie płatem kawałkami gładkim złożonym z płatów gładkich Σ1, Σ2, …, Σm oraz niech f będzie funkcją określoną i ograniczoną na płacie Σ. Całkę powierzchniową niezorientowaną z funkcji f po płacie Σ definiujemy wzorem:;
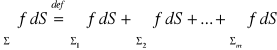
,
o ile całki po prawej stronie znaku równości istnieją.
Tw. 3.2.3 (liniowość całki powierzchniowej niezorientowanej)
Jeżeli funkcje f i g są całkowalne na kawałkami gładkim płacie powierzchniowym Σ oraz jeżeli c jest dowolną stałą, to:
![]()
,
![]()
.
Def. 3.2.4 (całka powierzchniowa niezorientowana z funkcji wektorowej)
Niech Σ będzie kawałkami gładkim płatem powierzchniowym oraz niech funkcje P, Q, R będą całkowalne na Σ. Całkę powierzchniową niezorientowaną po płacie Σ z funkcji wektorowej ![]()
określamy wzorem:
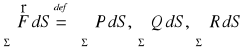
.
3.3 ZAMIANA CAŁKI POWIERZCHNIOWEJ NIEZORIENTOWANEJ NA CAŁKĘ PODWÓJNĄ
Tw. 3.3.1 (o zamianie całki powierzchniowej na całkę podwójną)
Jeżeli
1. obszar D ⊂ R2 jest regularny,
2. płat ![]()
jest gładki,
3. funkcja ![]()
jest ciągła,
to
![]()
.
Uwaga. Jeżeli płat gładki Σ jest wykresem funkcji z = z(x,y), gdzie (x,y) ∈ D oraz funkcja f jest ciągła na Σ, to wzór na zamianę całek przyjmuje postać:
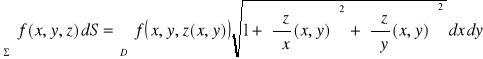
.
Analogiczne wzory otrzymujemy w przypadku płatów powierzchniowych opisanych równaniami x = x(y,z) lub y = y(x,z).
3.4 ZASTOSOWANIA CAŁEK POWIERZCHNIOWYCH NIEZORIENTOWANYCH
Fakt 3.4.1 (zastosowania w geometrii)
Pole kawałkami gładkiego płata Σ wyraża się wzorem:
![]()
.
Fakt 3.4.2 (zastosowania w fizyce)
![]()
.
|
|
|
![]()
,
![]()
,
![]()
.
![]()
, ![]()
, ![]()
.
|
|
|
![]()
,
![]()
,
![]()
,
![]()
.
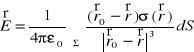
,
gdzie ε0 oznacza stałą dielektryczną próżni.
|
|
|
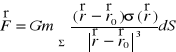
,
gdzie G oznacza stałą grawitacji.
Fakt 3.4.3 (środki masy płatów symetrycznych)
4. CAŁKI POWIERZCHNIOWE ZORIENTOWANE I ELEMENTY ANALIZY WEKTOROWEJ
4.1 DEFINICJA I WŁASNOŚCI CAŁKI POWIERZCHNIOWEJ ZORIENTOWANEJ
Def. 4.1.1 (płat powierzchniowy zorientowany)
Płat powierzchniowy dwustronny, na którym wyróżniono jedną ze stron, nazywamy płatem powierzchniowym zorientowanym. Wyróżnioną stronę płata zorientowanego nazywamy stroną dodatnią. Płat zorientowany oznaczamy tym samym symbolem co płat. Płat powierzchniowy zorientowany przeciwnie do płata zorientowanego Σ oznaczamy przez - Σ.
Dla płatów zamkniętych ograniczających pewien obszar w przestrzeni za stronę dodatnią płata przyjmujemy z reguły jego stronę zewnętrzną. Dla płatów będących wykresami funkcji postaci z = f(x,y), x = g(y,z), y = h(x,z) za stronę dodatnią przyjmujemy zwykle górną część takiego płata.
|
|
|
Rys. 4.1.1 Płat powierzchniowy jednostronny |
|
Rys. 4.1.2 Płat powierzchniowy dwustronny; wykres funkcji z = f(x,y) |
Fakt 4.1.2 (postać wersora normalnego płata)
Niech płat gładki zorientowany Σ ma przedstawienie parametryczne ![]()
. Wtedy wersor normalny ![]()
do płata Σ wystawiony w punkcie (x0, y0, z0) tego płata, odpowiadającym punktowi (u0, v0) obszaru D w powyższej parametryzacji wyraża się wzorem:

,
gdzie wektory ![]()
oraz ![]()
są obliczone w punkcie (u0, v0). Znak stojący przed wersorem ![]()
ustala się na podstawie orientacji płata Σ. Przyjmujemy, że wersor normalny jest skierowany od strony ujemnej do dodatniej płata zorientowanego.
Jeżeli płat gładki Σ jest wykresem funkcji z = z(x,y), gdzie (x,y) ∈ D, to wersor normalny ![]()
do płata Σ wystawiony w punkcie (x0, y0, z0) tego płata, gdzie z0 = z(x0, y0), wyraża się wzorem:
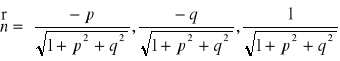
,
gdzie ![]()
, ![]()
. Wersor normalny ![]()
można przedstawić w postaci ![]()
, gdzie α, β, γ oznaczają kąty między tym wersorem, a dodatnimi częściami osi Ox, Oy, Oz.
|
|
|
||||
Rys. 4.1.3 Wersor normalny do płata zorientowanego Σ |
|
Rys. 4.1.4 Kosinusy kierunkowe wektora normalnego |
||||
Def. 4.1.3 (całka powierzchniowa zorientowana)
Niech ![]()
będzie polem wektorowym na płacie gładkim zorientowanym Σ. Całkę powierzchniową zorientowaną z pola wektorowego ![]()
po płacie Σ definiujemy wzorem:
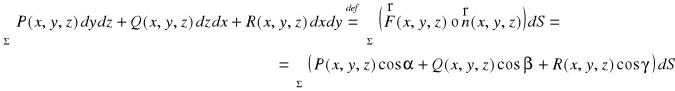
gdzie ![]()
oznacza wersor normalny do płata zorientowanego Σ wystawiony w punkcie (x,y,z) tego płata.
Uwaga. W zapisie wektorowym powyższa definicja przyjmuje postać:
![]()
,
gdzie ![]()
. Całkę powierzchniową zorientowaną z pola wektorowego ![]()
po płacie Σ oznaczamy też krótko ![]()
, a w notacji wektorowej ![]()
.
|
Rys. 4.1.5 Ilustracja do definicji całki powierzchniowej zorientowanej z pola wektorowego |
Def. 4.1.4 (całka powierzchniowa po płacie kawałkami gładkim)
Niech Σ będzie kawałkami gładkim płatem zorientowanym, utworzonym z płatów gładkich Σ1, Σ2, …, Σm, o orientacjach pokrywających się z orientacją płata Σ. Ponadto niech ![]()
będzie polem wektorowym określonym na płacie Σ. Całkę powierzchniową zorientowaną z pola wektorowego ![]()
po płacie Σ definiujemy wzorem:
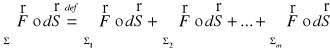
,
o ile całki po prawej stronie znaku równości istnieją. Jeżeli Σ jest płatem zorientowanym zamkniętym ograniczającym pewien obszar w przestrzeni, to wtedy piszemy ![]()
w miejsce ![]()
.
Tw. 4.1.5 (liniowość całki powierzchniowej zorientowanej)
Jeżeli istnieją całki powierzchniowe z pól wektorowych ![]()
i ![]()
po kawałkami gładkim płacie powierzchniowym zorientowanym Σ oraz jeżeli c jest dowolną stałą, to
![]()
,
![]()
,
![]()
.
4.2 ZAMIANA CAŁKI POWIERZCHNIOWEJ ZORIENTOWANEJ NA CAŁKĘ PODWÓJNĄ
Tw. 4.2.1 (o zamianie całki powierzchniowej na całkę podwójną)
Jeżeli
to
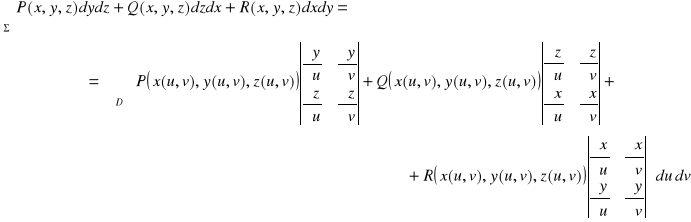
.
Znak stojący przed całką podwójną ustala się na podstawie orientacji płata Σ.
Uwaga. W zapisie wektorowym wzór ten przyjmuje postać
![]()
.
Jeżeli gładki płat zorientowany Σ jest wykresem funkcji z = z(x,y), gdzie (x,y) ∈ D, oraz pole wektorowe ![]()
jest ciągłe na Σ, to
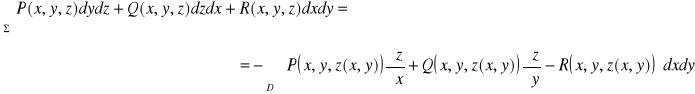
.
Podobne równości mają miejsce, gdy płat Σ jest wykresem funkcji x = x(y,z) lub y = y(x,z).
4.3 ELEMENTY ANALIZY WEKTOROWEJ
Def. 4.3.1 (operator Hamiltona - nabla)
Operator Hamiltona (nabla) określony jest wzorem:
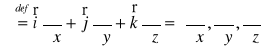
.
Def. 4.3.2 (gradient funkcji)
Niech f będzie funkcją różniczkowalną na obszarze V ⊂ R3. Gradient funkcji f jest określony wzorem:
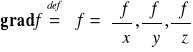
.
Fakt 4.3.3 (własności gradientu)
Niech funkcje f i g będą różniczkowalne na obszarze V ⊂ R3 oraz niech a, b ∈ R. Wtedy
Def. 4.3.4 (pole wektorowe potencjalne)
Pole wektorowe ![]()
nazywamy polem potencjalnym na obszarze V ⊂ R3, jeżeli istnieje funkcja ![]()
taka, że
![]()
.
Funkcję U nazywamy potencjałem pola wektorowego ![]()
.
Def. 4.3.5 (rotacja pola wektorowego)
Niech ![]()
będzie różniczkowalnym polem wektorowym określonym na obszarze V ⊂ R3. Rotację pola wektorowego ![]()
określamy wzorem:
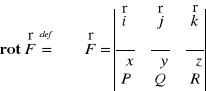
.
Fakt 4.3.6 (własności rotacji)
Niech f będzie funkcją różniczkowalną na obszarze V ⊂ R3 oraz niech pola wektorowe ![]()
i ![]()
będą różniczkowalne na tym obszarze. Wtedy
Def. 4.3.7 (dywergencja pola wektorowego)
Niech ![]()
będzie polem wektorowym różniczkowalnym w sposób ciągły na obszarze V ⊂ R3. Dywergencję pola wektorowego ![]()
określamy wzorem:
![]()
.
Fakt 4.3.8 (własności dywergencji)
Niech f będzie funkcją różniczkowalną w sposób ciągły na obszarze V ⊂ R3 oraz niech pola wektorowe ![]()
i ![]()
będą różniczkowalne w sposób ciągły na tym obszarze. Wtedy
4.4 TWIERDZENIE GAUSSA I STOKESA
Tw. 4.4.1 (wzór Gaussa)
Jeżeli
to
![]()
.
Po rozwinięciu powyższa równość (wzór Gaussa) przyjmuje postać:
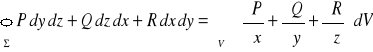
.
|
Rys. 4.4.1 Ilustracja do wzoru Gaussa |
Tw. 4.4.2 (wzór Stokesa)
Jeżeli
to
![]()
.
Po rozwinięciu powyższa równość (wzór Stokesa) przyjmuje postać:

.
|
Rys. 4.4.2 Ilustracja do wzoru Stokesa |
Uwaga. Wzór Greena podany w rozdziale 2.4 jest szczególnym przypadkiem wzoru Stokesa. Rzeczywiście, przyjmując, że Σ ⊂ xOy jest płatem zorientowanym o brzegu Γ oraz, że pole wektorowe ![]()
określone na tym płacie ma postać ![]()
, przy czym funkcje P i Q zależą tylko od zmiennych x, y, otrzymamy
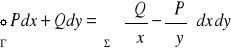
.
4.5 ZASTOSOWANIA CAŁEK POWIERZCHNIOWYCH ZORIENTOWANYCH
Fakt 4.5.1 (zastosowania w geometrii)
Objętość obszaru V ograniczonego płatem zamkniętym Σ zorientowanym na zewnątrz wyraża się wzorami:
![]()
.
Fakt 4.5.2 (zastosowania w fizyce)
![]()
,
gdzie ![]()
oznacza prędkość cieczy w punkcie (x,y,z) tego płata.
|
|
|
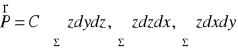
.
Wyszukiwarka