1. CEL ĆWICZENIA.

Zapoznanie się ze zjawiskiem Halla poprzez pomiary charakterystyk hallotronu.

2. WSTĘP TEORETYCZNY.

Jeżeli płytkę z metalu włączymy w obwód prądu stałego i umieścimy w polu magnetycznym , którego wektor indukcji B jest prostopadły do powierzchni płytki i do kierunku płynącego prądu elektrycznego , to między punktami A i B wytworzy się różnica potencjałów UH , zwana napięciem Halla , lub zjawiskiem galwanometrycznym ( RYS ).

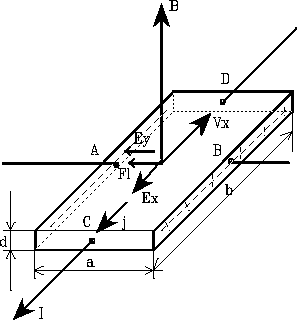
Załóżmy , że nośnikami prądu są elektrony. Jeżeli do punktów C i D przyłożymy napięcie , to w razie braku pola magnetycznego przez próbkę będzie płynąc prąd o natężeniu I. Wytworzone w próbce pole elektryczne o natężeniu Ex będzie skierowane zgodnie z kierunkiem płynącego prądu , natomiast elektrony poruszać się będą w kierunku przeciwnym polu z prędkością Vx. Gęstość prądu płynącego przez płytkę jest określona wzorem : j = e n Vx.

Natężenie prądu I można określić jako iloczyn gęstości prądu j i powierzchni S prostopadłej do wektora gęstości prądu
, czyli : I = e n Vx a d.

W obecności pola magnetycznego o indukcji B , na elektrony poruszające się w tym polu z prędkością Vx , działa siła Lorentza :

.

Tak więc każdy elektron w płytce , poruszający się z prędkością Vx , zostaje odchylony od swego początkowego kierunku ruchu zgodnie z powyższym wzorem. Wskutek zmiany torów elektrony gromadzą się na jednej krawędzi płytki , natomiast na drugiej wytwarza się niedobór elektronów. Dzięki temu powstaje pole elektryczne o natężeniu :

Proces gromadzenia się ładunków trwa tak długo , aż powstałe pole poprzeczne Ey , działające na elektrony z siłą : Fy = - e Ey , zrównoważy siłę Lorentza , czyli Fy = FL.

Pamiętając , że wektory Vx oraz B są do siebie prostopadłe oraz korzystając z powyższych zależności , otrzymujemy wyrażenie określające napięcie Halla :

, w którym
.

Mierząc natężenie prądu I płynącego przez płytkę , napięcie Halla UH oraz znając współczynnik , można wyznaczyć indukcję magnetyczną B.

Urządzenie służące do wyznaczania indukcji magnetycznej nazywa się HALLOTRONEM , współczunnik zaś nazywamy czyłóścią hallotronu.Zjawisku Halla towarzyszy wiele innych zjawisk fizycznych , które mogą wpływać na wartość mierzonego napięcia Halla. Jednym z nich jest zjawisko tzw. asymetrii pierwotnej , wiążące się z poprawnym wykonaniem elektrod hallowskich. Polega ono na tym , że gdy elektrody nie leżą dokładnie naprzeciwko siebie , tzn. nie leżą na tej samej powierzchni ekwipotencjalnej , wówczas gdy brak pola magnetycznego , lecz prąd I płynie przez hallotron , między elektrodami hallowskimi wytwarza się różnica potencjałów UA , zwana napięciem asymetrii pierwotnej , które sumuje się z napięciem Halla i utrudnia pomiar.

3. POMIARY.

3.1 Spis przyrządów : - elektromagnes EL - 01, - autotransformator,

- zasilacz elektromagnesu ZT - 980 - 4, - woltomierz cyfrowy V 530,

- miliamperomierze : LM - 1 , LM - 3,

- zasilacz ZT - 980 - 3,

- hallotron,

- adapter hallotronu.

3.2 Przebieg ćwiczenia.

Na wstępie należy usunąc ramkę z hallotronem z obszaru nabiegunnika magnesu , włączyć woltomierz V 530 oraz zasilacz ZT - 980 - 3. Następnie ustalamy prąd zasilania hallotronu IS = 5 mA oraz potencjometrem P umieszczonym w adapterze hallotronu kompensujemy napięcie asymetrii pierwotnej tak aby UH = 0 V.Wprowadzamy ramkę z hallotronem w obszar nabiegunników i obserwujemy wskazania V 530 , po czym włączamy zasilacz elektromagnesu.Przeprowadzamy pomiar zależności napięcia Halla od indukcji magnetycznej UH = f ( B ) przy ustalonym prądzie IS. Zależność indukcji magnetycznej B od prądu magnesującego Im odczytujemy na oddzielnym wykresie. Pomiary wykonujemy dla IS = 5 mA , a indukcję B zmieniamy od 0,1 0,5 T co 0,05 T.Drugim pomiarem jest zbadanie zależności napięcia Halla od prądu sterującego hallotronu UH = f ( IS ) przy ustalonej indukcji B = 0,5 T. Prąd IS zmieniamy od 1 5 mA co 0,5 mA.

3.3 Wyniki pomiarów.

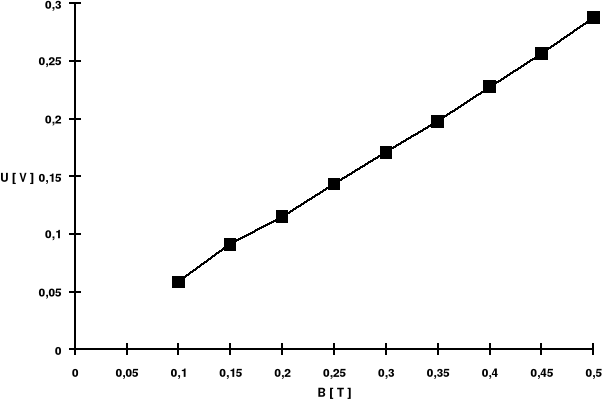
3.3.1 Zależność UH = f ( B ) , IS = const = 5 mA.

LP.	Im [ mA ]	UH [ mV ]	B [ T ]	[ V / ( A T ) ]
1.	30	58,5	0,10	117,0
2.	44	91,0	0,15	121,4
3.	59	114,8	0,20	114,8
4.	74	143,2	0,25	114,56
5.	89	170,8	0,30	113,87
6.	103	198,0	0,35	113,14
7.	118	227,9	0,40	113,95
8.	133	256,3	0,45	113,9
9.	148	287,5	0,50	115
				< > 115,3

CHARAKTERYSTYKA UH = f ( B ) ; IS = const

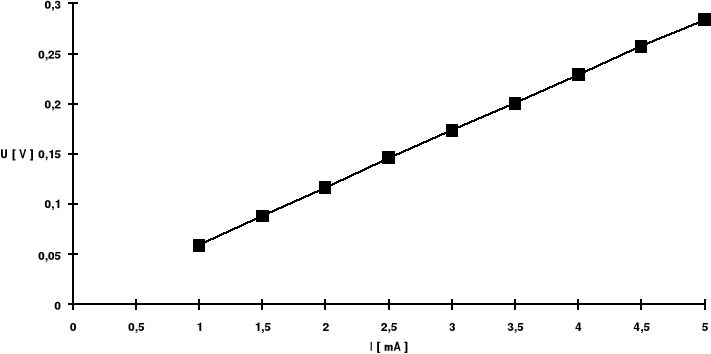
3.3.2 Zależność UH = f ( IS ) , B = const = 0,5 T

LP.	IS [ mA ]	UH [ mV ]	[ V / ( A T ) ]
1.	1	59,0	118
2.	1,5	88,2	117,6
3.	2	116,3	116,3
4.	2,5	146,3	117,04
5.	3	173,8	115,87
6.	3,5	200,6	114,63
7.	4	228,8	114,4
8.	4,5	257,1	114,27
9.	5	283,9	113,56
			< > 115,74

Z pomiarów 3.3.1 i 3.3.2 czułość hallotronu < > = 115,52.

CHARAKTERYSTYKA UH = f ( IS ) ; B = const

Koncentracja elektronów swobodnych w płytce hallotronowej obliczona ze wzoru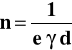
,

wynosi : 5,41 1020 , gdzie e = 1,6 10-19 C.

4. Analiza błędów.

Błąd UH / UH = UH = 0,05 % i IS / IS­ = IS = 0,5 % przyjmujemy na podstawie klasy użytych mierników.

Błąd cechowania elektromagnesu : B / B = B = 2 % .

Błąd pomiaru grubości hallotronu : d / d = d = 1 % .

Błędy i n obliczamy metodą pochodnej logarytmicznej :

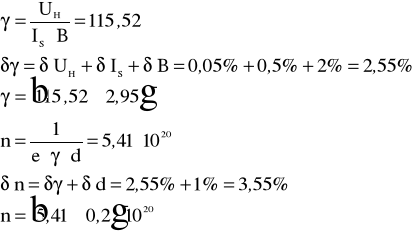
5. Uwagi i wnioski.

Hallotrony znalazły częste zastosowanie w miernictwie wielkości elektrycznych i nieelektrycznych :

- pomiar indukcji magnetycznej ,

- pomiar kąta obrotu ,

- pomiar mocy.

Efekt Halla obserwuje się także w półprzewodnikach.

Efekt Halla obserwuje się nie tylko w metalach , ale i w półprzewodnikach , gdzie ze znaku efektu można wnioskować o przynależności półprzewodnika do grupy n czy typu p.

Innym zastosowaniem hallotronu jest pomiar indukcji magnetycznej , bądź też pomiar kąta obrotu.

---