Wydz. Transportu			LABOLATORIUM PODSTAW ELEKTROTECHNIKI			Data:
Imię i nazwisko:				Grupa:	Zespół:	Rok akademicki:
Nr ćwiczenia:	Temat: Badanie obwodów trójfazowych.					Ocena:

Cel ćwiczenia:

Celem ćwiczenia jest analiza rozkładu napięć, prądów i mocy odbiorników trójfazowych symetrycznego oraz niesymetrycznego, połączonych w gwiazdę.

Układem trójfazowym nazywamy układ rozgałęziony, w którym działają napięcia źródłowe sinusoidalne o jednakowej częstotliwości, przesunięte względem siebie w fazie. W przypadku gdy napięcia źródłowe w poszczególnych fazach mają równe wartości skuteczne i przesunięte są względem siebie o kąt 120° to tworzą one układ symetryczny. Jeżeli układ napięć źródłowych jest niesymetryczny lub impedancje obciążenia poszczególnych faz nie są jednakowe, to układ taki nazywamy niesymetrycznym. Gdy układ jest symetryczny to napięcia międzyfazowe są razy większe od napięć fazowych.

Moc dla odbiornika symetrycznego:

P = 3 U_f I_f cosϕ_f = U_p I_p cosϕ_f = 3 R I_f²

Q =3 X I_f² = U_p I_p sinϕ_f

gdzie:

U_f , I_f - Napięcie i prąd fazowy ;

U_p , I_p - Napięcie i prąd przewodowy ;

cosϕ_f - cosinus kąta między prądem a napięciem jednej fazy.

Przebieg ćwiczenia:

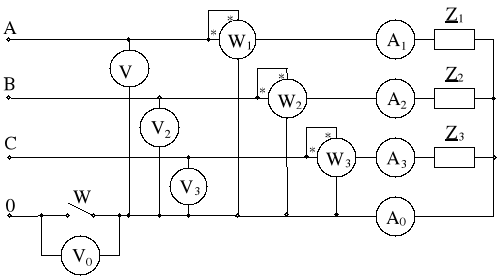
Tabela pomiarowa

Odbiornik		Pomiary											Obliczenia
	Przew.	UA	UB	UC	U0	IA	IB	IC	I0	PA	PB	PC	P	Q	S
	zerowy	V	V	V	V	A	A	A	A	W	W	W	W	var	VA
symetr.	tak	100	100	100	0	0,25	0,25	0,25	0	15	15	15	45	32	41
	nie	100	100	100	0	0,25	0,25	0,25	0	15	15	15	45	34	41
niesym.	tak	100	100	100	0	0,25	0,25	0,4	0,23	15	15	40	70	49	75
	nie	130	90	90	29	0,33	0,22	0,35	0.05	27	11	32	70	49	75
przerw	tak	100	100	100	0	0,25	0,25	0	0,23	16	15	0	38	23	42
	nie	96	80	116	37	0,24	0,19	0	0,07	15	9	0	24	19	32
zwarcie	nie	132	0	172	100	0,44	0,82	0,42	0,05	47	0	43	90	56	96

X_n = Z_n sin ϕ_n

Q = U_n I_n sin ϕ_n

P = P_A+P_B+P_C

gdzie: n - kolejna faza A, B, C

1) Odbiornik symetryczny:

Parametry układu: R₁=R₂=R₃=217Ω

Z przewodem zerowym:

R_A=211 Ω R_B=212 Ω R_C=211 Ω

cosϕ_A=0,97 cosϕ_B=0,95 cosϕ_C=0,97

ϕ_A=14 ° ϕ_B=17 ° ϕ_C=14 °

Q_A=16 var Q_B=19 var Q_C=16 var

S_A=66 VA S_B=64,8 VA S_C=66 VA

Bez przewodu zerowego:

R_A=214,8 Ω R_B=219,4 Ω R_C=181 Ω

cosϕ_A=0,98 cosϕ_B=0,98 cosϕ_C=0,88

ϕ_A=11,4 ° ϕ_B=11,4 ° ϕ_C=28,3 °

Q_A=13 var Q_B=12,8 var Q_C=33,56 var

S_A=66,3 VA S_B=65,26 VA S_C=71,38 VA

2) Odbiornik niesymetryczny:

Parametry układu: R₁=217Ω; R₂=180Ω; R₃=150Ω; R_L=18,1Ω; L=0,29H

Z przewodem zerowym:

R_A=225 Ω R_B=130 Ω R_C=144,2 Ω

cosϕ_A=0,92 cosϕ_B=0,7 cosϕ_C=0,94

ϕ_A=23 ° ϕ_B=45,5 ° ϕ_C=20 °

Q_A=23 var Q_B=55,63 var Q_C=32,42 var

S_A=58,7 VA S_B=78,22 VA S_C=95,66 VA

Bez przewodu zerowego:

R_A=231,4 Ω R_B=215 Ω R_C=141,6 Ω

cosϕ_A=0,94 cosϕ_B=0,99 cosϕ_C=0,93

ϕ_A=20 ° ϕ_B=8,1 ° ϕ_C=21,5 °

Q_A=25,4 var Q_B=11,34 var Q_C=22,75 var

S_A=74,46 VA S_B=80,8 VA S_C=62,3 VA

3) Odbiornik niesymetryczny - przerwa w fazie C

Parametry układu: R₁=217Ω; R₂=180Ω; R₃=150Ω; R_L=18,1Ω; L=0,29H

Z przewodem zerowym:

R_A=212,4 Ω R_B=175,1 Ω R_C= ∞ Ω

cosϕ_A=0,86 cosϕ_B=0,94 cosϕ_C= 0

ϕ_A=30,6 ° ϕ_B=20 ° ϕ_C=90 °

Q_A=30 var Q_B=26,67 var Q_C=0 var

S_A=59,16 VA S_B=78,65 VA S_C=0 VA

Bez przewodu zerowego:

R_A=225 Ω R_B=175 Ω R_C= ∞ Ω

cosϕ_A=0,84 cosϕ_B=0,93 cosϕ_C= 0

ϕ_A=32,8 ° ϕ_B=21,5 ° ϕ_C=90 °

Q_A=34,5 var Q_B=16,52 var Q_C=0 var

S_A=64 VA S_B=45,13 VA S_C=0 VA

4. Odbiornik niesymetryczny - zwarcie w fazie C

Parametry układu: R₁=217Ω; R₂=180Ω; R₃=150Ω; R_L=18,1Ω; L=0,29H

Bez przewodu zerowego:

R_A=246,8 Ω R_B=175,3 Ω R_C= 0 Ω

cosϕ_A=0,96 cosϕ_B=0,93 cosϕ_C= 0

ϕ_A=16,2 ° ϕ_B=21,5 ° ϕ_C=90 °

Q_A=45,75 var Q_B=86,2 var Q_C=0 var

S_A=164,5 VA S_B=236,2 VA S_C=0 VA

Wykres dla odbiornika symetrycznego z przewodem zerowym.

Wykres dla odbiornika z przerwą w fazie

Wykres dla odbiornika niesymetrycznego z przewodem zerowym

Wykres dla odbiornika niesymetrycznego bez przew. zerowego

Wykres dla odbiornika z przew. zerowym z przerwą wfazie C

Zwarcie w fazie C

Wnioski

Zgodnie z celem ćwiczenia dokonaliśmy analizy rozkładu prądów i napięć w układzie trójfazowym połączonym w gwiazdę. W przypadku obwodów trójfazowych symetrycznych połączonych w gwiazdę cosinus przesunięcia fazowego jest w przybliżeniu równy 1. Natomiast w obwodach niesymetrycznych, szczególnie dla przerwy lub zwarcia w jednej z faz, cosinus może znacznie odbiegać od jedynki. W przypadku zwarcia w jednej z faz wzrasta pobór prądu co powoduje wzrost poboru mocy w pozostałych fazach.

Dla symetrycznego odbiornika w układzie z przewodem zerowym zauważyliśmy przepływ bardzo małego prądu wyrównawczego, a bez przewodu zerowego - małe napięcie niesymetrii. Dla odbiornika niesymetrycznego w przewodzie zerowym płynie dosyć duży prąd uzależniony od różnic w impedancji poszczególnych odbiorników, zaś bez przewodu występuje duże napięcie niesymetrii, co powoduje zakłócenie warunków zasilania odbiorników. W układach elektroenergetycznych stosowanych w praktyce może to doprowadzić w skrajnych przypadkach nawet do uszkodzenia odbiornika, gdyż napięcie fazowe może osiągnąć wartość zbliżoną do napięcia międzyfazowego, szczególnie w przypadku zwarcia w jednej z faz.

7

Ib

Ic

Ia

Ucc

Ec

Ub

Eb

Ua

Ea

Ib

Ib+Ia=Io

Ia

Ec=Uc

Ea=Ua

Eb=Eb

-I_B

I_C

I_A

U_C

U_A

E_B=U_N

E_C

E_A

---