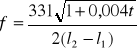Uniwersytet Śląski Wydział Techniki Sosnowiec	Sprawozdanie z zajęć laboratoryjnych	Wychowanie Techniczne	Semestr III	Sprawdził
					28.10.2001 r
			Temat: Wyznaczanie prędkości rozchodzenia się dźwięku w ciele stałym oraz modułu Younga przy pomocy rury Kunda
		Instytut Problemów Techniki
							Kozielski Piotr		Ocena
Zakład

WSTĘP TEORETYCZNY

FALE, zaburzenia pól fiz. rozchodzące się ze skończoną prędkością i przenoszące energię. Ze względu na fiz. naturę zachodzących zjawisk rozróżnia się: fale polegające na mech. przemieszczaniu się elementów ośr. (np. fale sprężyste), fale elektromagnetyczne (np. światło, fale radiowe), które są zaburzeniami pola elektromagnet., fale grawitacyjne (stanowiące zaburzenia pola grawitacyjnego), fale de Broglie'a (zw. też falami materii), związane z poruszającymi się mikrocząstkami materii (np. elektronami, neutronami, atomami). Powyższy podział jest b. uproszczony — nie obejmuje m.in. pewnych specyficznych fal w plazmie (np. fal magnetohydrodynamicznych, zw. też falami Alfvéna). Rozchodzenie się fal opisuje równanie falowe; dla fal sprężystych równanie to wynika z równań ruchu Newtona, dla fal elektromagnet. z równań Maxwella, fale de Broglie'a (w przybliżeniu nierelatywistycznym) opisuje równanie Schrödingera. W najprostszym przypadku fali jednowymiarowej (np. na sprężystej strunie) równanie falowe ma postać:
, gdzie  (x, t) — funkcja falowa — funkcja opisująca zależność zaburzenia od zmiennych przestrzennych i czasu, v — prędkość przemieszczania się zaburzenia. Z punktu widzenia zależności czasowej zaburzenia wyróżnia się: impulsy falowe, w których zaburzenie w określonym punkcie trwa przez określony czas, oraz fale harmoniczne, w których w określonym punkcie zaburzenie zmienia się w czasie t periodycznie. Wśród fal harmonicznych ważną grupę stanowią fale sinusoidalne: biegnące — w których zaburzenie przemieszcza się w przestrzeni, i stojące (w falach tych wyróżnia się punkty, w których zaburzenie stale znika — tzw. węzły, i punkty, w których zaburzenie ma w określonej chwili wartość maks. — tzw. strzałki). Fale biegnące w przypadku jednowymiarowym opisuje funkcja falowa (x, t) = A cos (kx - t), dla fal de Broglie'a (x, t) = Ae ^{i (kx - t)}, gdzie A jest amplitudą fali a argument (kx - t) określa fazę fali;  — częstość kołowa fali, k = 2/ — liczba falowa,  — długość fali, czyli najmniejsza odległość między punktami o takiej samej fazie zaburzenia. Fale, w których punkty jednakowego zaburzenia (ściślej, jednakowej fazy), czyli powierzchnia falowa, wyznaczają w przestrzeni płaszczyznę, są zw. falami płaskimi, sferę — falami kulistymi, powierzchnię cylindryczną — falami cylindrycznymi. Powierzchnia falowa fali harmonicznej przemieszcza się z prędkością fazową v =  (  = /2 — częstość fali). Z punktu widzenia charakteru zaburzenia rozróżnia się fale skalarne (w których zaburzenie jest opisane funkcją skalarną, np. ciśnienie w gazie), fale wektorowe, w których zaburzenie opisuje funkcja wektorowa (np. natężenie pola elektr.) i fale spinorowe (fale de Broglie'a dla elektronów z uwzględnieniem spinu). Fale, w których kierunek zaburzenia jest równoległy do kierunku rozchodzenia się fal, są falami podłużnymi (np. fale dźwiękowe w powietrzu), zaś fale, w których kierunek zaburzenia jest prostopadły do kierunku rozchodzenia się fal — falami poprzecznymi (np. fale elektromagnet. w próżni, fale na powierzchni wody); istnieją też fale wektorowe, które nie należą do żadnej z tych grup, np. fale sprężyste w kryształach, fale elektromagnet. w kryształach dwójłomnych. Z ruchem falowym wiąże się wiele charakterystycznych zjawisk, jak np.: interferencja fal, dyfrakcja fal, rozpraszanie fal, dyspersja fal, odbicie i załamanie fal, absorpcja fal; z falami nieskalarnymi łączą się ponadto zjawiska polaryzacji fal.

Polaryzacja fali. W fali niespolaryzowanej drgania zachodzą we wszystkich kierunkach prostopadłych do promienia fali (wyznaczającego kierunek jej rozchodzenia się), w fali spolaryzowanej liniowo — w jednej, ściśle określonej płaszczyźnie.

FALE SPRĘŻYSTE, fale akustyczne, rozchodzące się w ośr. materialnym zaburzenia stanu naprężeń (ciśnień); ruch falowy w tym przypadku polega na przenoszeniu energii mech. cząstek drgających wokół swych położeń równowagi; prędkość przenoszenia energii (rozchodzenia się zaburzenia, czyli prędkość rozchodzenia się fal sprężystych) zależy od rodzaju ośr., temperatury, kierunku rozchodzenia się fali (w ośr. anizotropowych) i jest nazywana prędkością dźwięku w danym ośr.; prędkość ta wynosi w gazach — kilkaset m/s (w powietrzu w temp. 20°C — ok. 340 m/s), w wodzie ok. 1500 m/s, w ciałach stałych kilka tys. m/s. Fale sprężyste mogą być podłużne i poprzeczne (fale); zależnie od częstości dzielą się na infradźwięki, dźwięki, ultra- i hiperdźwięki. Fale sprężyste podłużne i poprzeczne we wzajemnym oddziaływaniu mogą tworzyć inne rodzaje fal, np. fale skrętne, fale giętne (obserwowane w blachach, prętach itp.); fale sprężyste rozchodzące się w skorupie Ziemi noszą nazwę fal sejsmicznych.

Odmianą fal sprężystych są fale powierzchniowe, rozchodzące się na powierzchni ograniczającej ośrodek (stały, ciekły). Rozróżnia się: fale Rayleigha (na swobodnej powierzchni cieczy lub ciała stałego graniczącego z próżnią lub gazem), fale Stonleya (na powierzchni rozdzielającej 2 ośr. stałe), fale Lamba (płytowe, rozchodzące się w blachach, płytach itp., których grubość jest porównywalna z długością fali), fale Love'a (fale poprzeczne rozchodzące się w warstwach na stałym podłożu) i in. Fale sprężyste powierzchniowe z zakresu częstości ultra- i hiperdźwiękowych (a więc o długościach rzędu metra i ułamków metra) można wytwarzać na powierzchni małych elementów (np. o właściwościach piezoelektr.) i wykorzystywać w wielu układach elektron. (akustoelektronika, akustooptyka).

DŹWIĘK, zaburzenia falowe w ośr. sprężystym, gazowym, ciekłym i stałym (fale, fale sprężyste) zdolne do wywołania wrażenia słuchowego, a także wrażenie słuchowe wywołane tym zjawiskiem. Dźwięk zatem — to zachodzące z odpowiednią częstością zmiany ciśnienia w ośr. (ciśnienie akustyczne), na które reaguje organ słuchu. Ucho ludzkie reaguje na względną zmianę poziomu dźwięku (wyrażaną na ogół w decybelach, dB). Najniższa wartość ciśnienia akust. (przy częst. 1000 Hz) wykrywanego przez ucho ludzkie wynosi średnio 20 µPa (próg słyszalności); 20 Pa — to próg bólu. Częstości fal dźwiękowych zawierają się w granicach 16 Hz-20 kHz. Fale sprężyste o częstościach wyższych nazywa się ultradźwiękami, a o częstościach niższych — infradźwiękami; fale o częst. 10⁹ Hz i wyższej stanowią hiperdźwięki. Źródłem dźwięku są drgające ciała stałe (np. struny, membrany) oraz zawirowania powietrza. Zagadnienia wytwarzania, rozchodzenia się i odbioru dźwięku są przedmiotem badań akustyki.

Fizycznymi wielkościami określającymi dźwięk są: ciśnienie akust., natężenie dźwięku, widmo dźwięku oraz częstość składowej podstawowej w tym widmie lub częstość czystego tonu. Wielkościom tym odpowiadają cechy subiektywne: natężeniu — głośność dźwięku, częstości podstawowej — wysokość, a widmu — barwa dźwięku. Dźwięki długotrwałe dzielą się na tony (dźwięki harmoniczne, sinusoidalne, o jednej częstości) i złożone z tonów — wielotony i szumy; wśród dźwięków krótkotrwałych (impulsów) rozróżnia się stuki i trzaski. W przeciwieństwie do szumów, stuków i trzasków tony i wielotony są odczuwane jako dźwięki o określonej wysokości.

INTERFERENCJA FAL, nakładanie się 2 lub więcej fal prowadzące do zwiększenia lub zmniejszenia amplitudy fali wypadkowej w zależności od różnicy faz fal składowych. Gdy częstości są jednakowe, a różnica faz fal w każdym punkcie jest stała w czasie (fale są spójne), to otrzymuje się niezmienny w czasie rozkład amplitud w przestrzeni z następującymi po sobie maksimami i minimami. Interferencja fal ugiętych może prowadzić do powstania charakterystycznych obrazów dyfrakcyjno-interferencyjnych (dyfrakcja fal). W wyniku interferencji fal o nieco różnych częstościach powstają dudnienia, w wyniku zaś interferencji fal bieżącej i odbitej — fala stojąca. Interferencja jest zjawiskiem charakterystycznym dla każdego ruchu falowego. Szczególnie duże znaczenie ma interferencja światła. Interferencja fal radiowych, powstająca w wyniku nakładania się fal dochodzących bezpośrednio od anteny z falami ugiętymi i odbitymi (np. od powierzchni Ziemi, jonosfery), stanowi często źródło zakłóceń odbioru radiowego; wykorzystywana niekiedy do uzyskania żądanej charakterystyki kierunkowej. Interferencję fal rentgenowskich ugiętych na atomach wykorzystuje się do badania struktury ciał krystal., zaś interferencję fal akustycznych — m.in. do pomiaru współczynnika pochłaniania materiałów dźwiękochłonnych oraz do pomiaru prędkości ultradźwięków.

YOUNGA MODUŁ, moduł sprężystości podłużnej, E, wielkość określająca własności sprężyste ciała stałego; w prawie Hooke'a występuje jako współczynnik proporcjonalności między naprężeniem i odkształceniem; nazwa pochodzi od nazwiska Th. Younga; dla stali moduł Younga wynosi ok. 2 · 10⁵ MPa, dla brązu — ok. 1 · 10⁵ MPa, dla szkła — ok. 0,6 · 10⁵ MPa.

SZTYWNOŚĆ, wielkość określająca zdolność ciała do przeciwstawiania się odkształceniu wywołanemu przez obciążenie zewn.; sztywność zależy od kształtu ciała, własności sprężystych materiału, rodzaju obciążenia (rozciąganie, zginanie, skręcanie); rozróżnia się sztywność przy rozciąganiu (ściskaniu) — iloczyn modułu sprężystości podłużnej i pola poprzecznego przekroju pręta, przy zginaniu — iloczyn modułu sprężystości podłużnej i osiowego momentu bezwładności, przy skręcaniu — iloczyn modułu sprężystości poprzecznej i biegunowego momentu bezwładności; wielkość odkształcenia jest odwrotnie proporcjonalna do sztywności.

MODUŁ SZTYWNOŚCI-Deformacja jest to względna zmiana rozmiarów ciala.

D=∆w/w_o ,gdzie ∆w to zmiana rozmiarów ciała a w_o to rozmiar początkowy.

Dla niewielkich deformacji kąty θ są małe i można przyjąć, że tgθ=θ.

Gdy D=∆w/w_o→D=tgθ to moduł sztywności wynosi G= σ/θ ,σ to naprężenie.

W każdym ośrodku sprężystym drgania wzbudzone w jednym miejscu rozchodzą się do miejsc coraz dalszych z prędkością υ, charakterystyczną dla danego ośrodka.

Czas w ciągu, którego wykonane jest jedno pełne drganie nosi nazwę okresu T. Jego wartość zależna jest od częstotliwości drgań ν:

Zjawisko rozchodzenia się drgań nazywamy falą.

Długością fali λ nazywamy odległość, na jaką fala przesuwa się w czasie jednego okresu T; jest to zarazem odległość między dwoma najbliższymi punktami fali, które mają taką samą fazę. Ponieważ fala rozchodzi się ruchem jednostajnym, więc na podstawie równania tego ruchu otrzymujemy długość fali

lub

Fale poprzeczne - cząstki drgają prostopadle do kierunku rozchodzenia (przemieszczania) się fali

Fale podłużne - cząstki drgają wzdłuż linii po której biegnie fala

Interferencja - nakładanie się fal o tych samych częstotliwości i amplitudach, ale innych fazach. Amplituda nałożonych fal zależy od różnicy faz.

Fala stojąca - posiada punkty, które znajdują się w ciągłym spoczynku - są to węzły fali. Wszystkie punkty między węzłami mają tę samą (w danej chwili) fazę drgań , lecz różne amplitudy.

Węzły - występują w miejscach gdzie nie ma drgań,

dla których 2Acos2π/λ = 0 czyli dla x = (2n+1)λ/4

odległość pomiędzy węzłami wynosi λ/2

Strzałki -występują w miejscach gdzie drgania mają największą amplitudę,

dla których 2Acos2π/λ = ±1 czyli dla x = nλ/2

odległość pomiędzy strzałkami wynosi λ/2

Moduł Younga (E) - Przesówanie się fali podłużnej związane jest z rozchodzeniem się zagęszczeń i rozrzedzeń ośrodka; prędkość v_x rozchodzenia się fali podłużnej w pręcie winna zatem zależeć od jego modułu sprężystości decydującego o rozciąganiu i ściskaniu jednostronnym pręta, tzn od jego modułu Younga E. Oprócz własności sprężystych ośrodka, wpływwających na prędkość v_x, prędkośc tę warunkuje jeszcze bezwładność cząsteczek ośrodka, której miarą jest gęstośc d materiału pręta. Wpływ tych dwu wielkości (E,d) na prędkośc fali podłużnej znajduje wyraz we wzorze: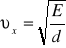

Mając wyznaczone v_x dla danego materiału możemy wyznaczyć jego moduł Younga ( wartość d odczytujemy z tablic):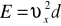

Rura Kundta

Występowanie fali stojącej może być wykorzystane do pomiaru prędkości dźwięku w danym ośrodku. Jeżeli fala dźwiękowa o częstotliwości f przechodzi z jednego ośrodka do drugiego, wówczas zmienia się prędkość fali υ i jej długość λ, natomiast częstość drgań pozostaje bez zmiany. Dla obu ośrodków słuszne są więc równania:

Z czego otrzymujemy zależność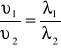

Prędkość fali dźwiękowej w powietrzu możemy przyjąć za znaną, gdyż jej wyznaczenie jest względnie łatwe.

Prędkość fali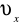
w ośrodku badanym można wyznaczyć ze wzoru:

Prędkość fali dźwiękowej w powietrzu w temperaturze t przedstawia wzór:

=331m/sek.

λ=0,004 1/K

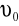
t=22°C= 295K

Wzory wg., których dokonano obliczeń:

Nazwa Materiału

Długość pręta L - cm

Fala Stojąca w powietrzu

Prędkość fali w pręcie v­­­­­x

Gęstość materiału d

Moduł Younga E

Odległość między skrajnymi węzłami L

Liczba połówek fali n

Długość połowy fali a

Wartość średnia a

Aluminium

102cm

30,6cm

4

7,65cm

6516,2m/s

0,0027

114644,6

23,5cm

3

7,83cm

6366,4m/s

109434,2

38,2cm

6

6,36cm

7837,9m/s

165867,9

7,28cm

6847,4m/s

126594,2

Wartość średnia v­­x

6906,8m/s

128800,4

102cm

38,1cm

4

9,5cm

6247,3m/s

105377,6

21,1cm

3

7cm

7121,3m/s

136921,3

42,5cm

6

7cm

7121,3m/s

136921,3

7,8cm

6390,9m/s

110277,6

Wartość średnia v­­x

6496,6m/s

113956,9

Rura Quinckego

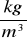
Warunek rezonansu: zgodność częstotliwości drgań pobudzających z częstotliwością drgań własnych słupa powietrza, zależnych od długości tego słupa.

W przypadku rury o zmieniającej się długości rezonansu ,fala dźwiękowa, występuje zawsze wówczas gdy rura jest tak długa, że na zamkniętym końcu może powstać węzeł, a na otwartym strzałka fali stojącej, tzn. gdy długość rury l jest równa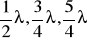
,.... czyli nieparzystej wielokrotności ¼ długości fali. Ogólny warunek rezonansu ma więc postać:

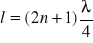
gdzie n=0,1,2,3,...

Mierząc długość l rury w czasie rezonansu można wyznaczyć długość λ fali w powietrzu.

Prędkość fali dźwiękowej w powietrzu wyrażamy:

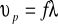
a więc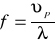

Z czego otrzymujemy równanie przy pomocy którego obliczamy częstotliwość drgań

Generator w pozycji A1

Pozycja I rezonansu		l1.1= 12,8cm	l1.2= 13,0cm
Wartość średnia		12,9cm
Pozycja II rezonansu		l2.1= 17,2cm	l2.1= 17,0cm
Wartość średnia		17,1
Długość fali źwiękowej		8,8cm	8cm
	Średnia	8,4cm
Temperatura powietrza		22°C
Prędkość dźwięku w powietrzu		488,7m/s
Częstotliwość drgań		2776,7	3054,4
	Średnia	2908,9

Generator w pozycji A2

Pozycja I rezonansu			l1.1= 11,5cm	l1.2= 11cm
Wartość średnia			11,25cm
Pozycja II rezonansu			l2.1= 21,5cm	l2.1= 22cm
Wartość średnia			21,1cm
Długość fali dźwiękowej			20 cm	22 cm
	Średnia		21cm
Temperatura powietrza			22°C
Prędkość dźwięku w powietrzu			488,7m/s
Częstotliwość drgań			1629	1546,5
		Średnia	1629

Generator w pozycji A3

Pozycja I rezonansu		l1.1= 15,1cm	l1.2= 14,5cm
Wartość średnia		14,8cm
Pozycja II rezonansu		l2.1= 22,5cm	l2.1= 23,1cm
Wartość średnia		22,8 cm
Długość fali dźwiękowej		15cm	16cm
	Średnia	8,3cm
Temperatura powietrza		22°C
Prędkość dźwięku w powietrzu		488,7m/s
Częstotliwość drgań		2908,9	2908,9
	Średnia	2943,9

Generator w pozycji B1

Pozycja I rezonansu		l1.1= 14,5cm	l1.2= 15,0cm
Wartość średnia		14,75cm
Pozycja II rezonansu		l2.1= 22,5cm	L2.1= 23,0cm
Wartość średnia		22,75
Długość fali źwiękowej		16,0cm	16,0cm
	Średnia	16,0cm
Temperatura powietrza		23°C
Prędkość dźwięku w powietrzu		488,7m/s
Częstotliwość drgań		2776,7	3054,4
	Średnia	2908,9

Generator w pozycji B2

Pozycja I rezonansu			l1.1= 10,5cm	l1.2= 10cm
Wartość średnia			10,25cm
Pozycja II rezonansu			l2.1= 18,5cm	l2.1= 19cm
Wartość średnia			18,75cm
Długość fali dźwiękowej			16,0 cm	18,0 cm
	Średnia		17cm
Temperatura powietrza			23°C
Prędkość dźwięku w powietrzu			488,7m/s
Częstotliwość drgań			1629	1546,5
		Średnia	1629

Generator w pozycji B3

Pozycja I rezonansu		l1.1= 14,5cm	L1.2= 15,0cm
Wartość średnia		14,75cm
Pozycja II rezonansu		l2.1= 26,0cm	L2.1= 25,5cm
Wartość średnia		25,75 cm
Długość fali dźwiękowej		23,0cm	21,0cm
	Średnia	22,0cm
Temperatura powietrza		23°C
Prędkość dźwięku w powietrzu		488,7m/s
Częstotliwość drgań		2908,9	2908,9
	Średnia	2943,9

---