Sprawozdanie z laboratorium

Podstaw i Algorytmów Przetwarzania Sygnałów

• ILOCZYN SKALARNY

Wykorzystując skrypt ilskal.m obliczony został iloczyn skalarny sygnałów: sinusa i cosinusa.

iloczyn skalarny funkcji sinus i cosinus (metoda 1) = -0.000075

czas wykonania (metoda 1) = 1.211999

iloczyn skalarny funkcji sinus i cosinus (metoda 2) = -0.000075

czas wykonania (metoda 1) = 0.034001

Funkcje sinus i cosinus są wzajemnie niezależne (ortogonalne), ponieważ iloczyn skalarny jest bliski zeru.

• SPLOT

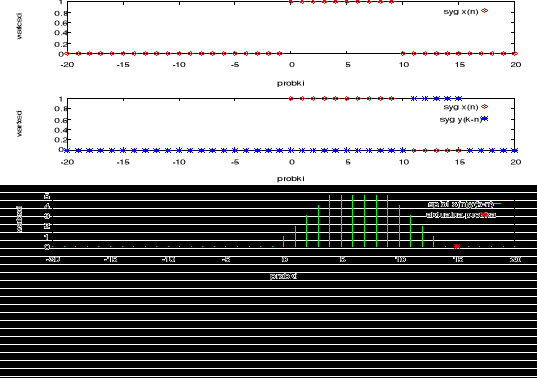
Wykorzystując skrypt convdemo.m wyznaczono splot dwóch sygnałów prostokątnych. Obrazuje to rysuunek1. Długość splotu dwóch sygnałów jest równy sumie ich długości minus 1.

Rysunek 1 Wynik splotu dwóch sygnałów prostokątnych.

Następnie dokonano obserwacji splotu sygnału prostokątnego z sygnałem trójkątnym. Obrazuje to poniższy rysunek 2.

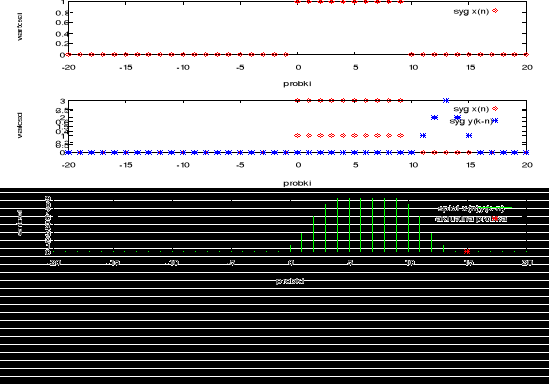
Rysunek 2 Wynik splotu sygnału prostokątnego i trójkątnego.

Poniżej przedstawione jest działanie skryptu conv_mx. Skrypt ten dokonuje splotu sygnału mowy z odpowiedzią impulsową filtru FIR. Rysunek 3 przedstawia wynik splotu w dziedzinie czasu, a rysunek 4 w dziedzinie częstotliwości.

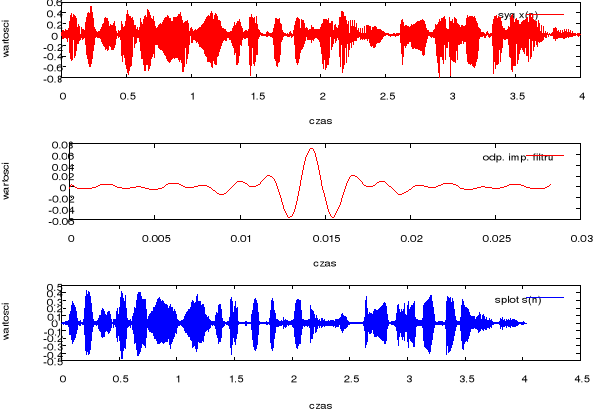
Rysunek 3 Wynik splotu sygnału mowy z odpowiedzią impulsową filtru FIR w dziedzinie czasu.

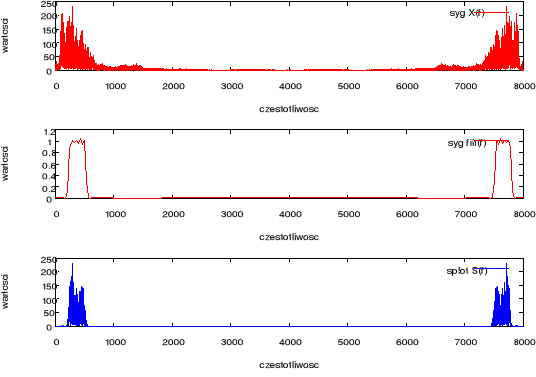
Rysunek 4 Wynik splotu sygnału mowy z odpowiedzią impulsową filtru FIR w dziedzinie częstotliwości.

Odsłuchując sygnał mowy przed i po splocie, stwierdzono, że sygnał spleciony z odpowiedzią impulsową filtru FIR jest zniekształcony i cichszy.

• KORELACJA

W tej części ćwiczenia wyznaczono autokorelację sygnału sinusoidalnego (rys.5)

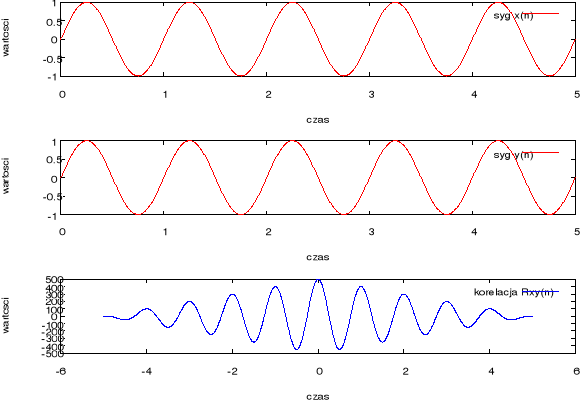
Rysunek 5 Wykres autokorelacji sygnału sinusoidalnego.

Następnie dodano szum do sygnału sinusoidalnego, co możemy zaobserwować na rysunku 6. Korelacja tych dwóch sygnałów jest identyczna jak sygnałów niezaszumonych.

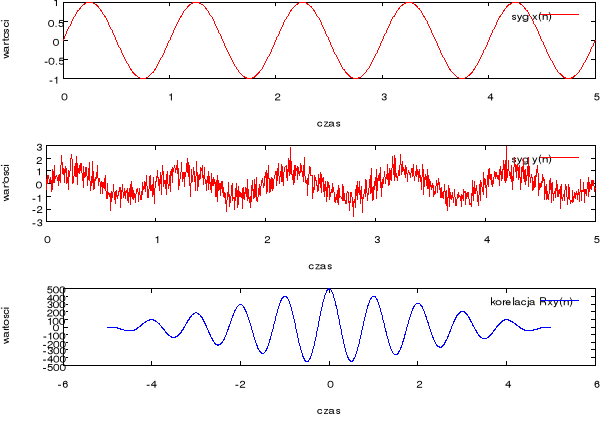
Rysunek 6 Wykres korelacji sygnału sinusoidalnego i sinusoidalnego zaszumionego.

Poniżej przedstawiona jest autokorelacja szumu. Ponieważ oba sygnały są identyczne, wykres korelacji z wykresu możemy odczytać brak przesunięcia w czasie.

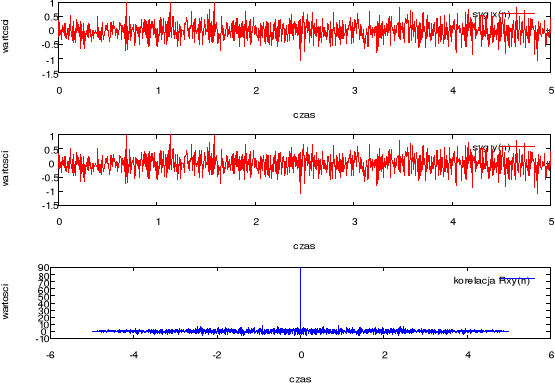
Rysunek 7 Wykres obrazujący autokorelację szumu.

Poniższy rysunek 8 przedstawia autokorelację dwóch identycznych sygnałów chirp. Ponieważ są one przesunięte w czasie, fakt ten możemy zaobserwować na wykresie korelacji.

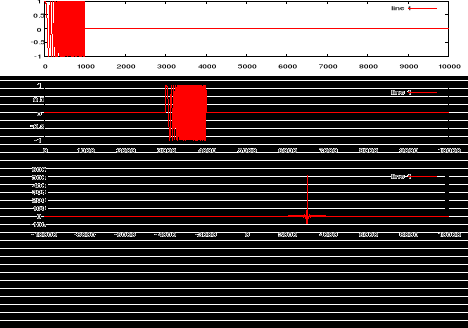
Rysunek 8 Korelacja dwóch identycznych sygnałów przesuniętych w czasie.

Jeżeli do powyższych sygnałów dodamy szum, wykres korelacji zmieni nieznacznie swój wygląd. Sygnały zaszumione są bardziej skorelowane ze sobą również w okolicach braku przesuniecia.

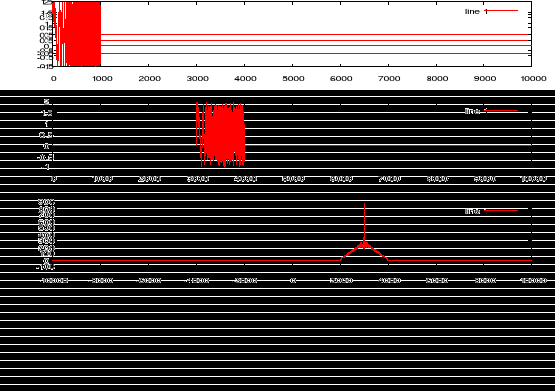
Rysunek 9 Korelacja dwóch identycznych, zaszumionych sygnałów przesuniętych w czasie.

WNIOSKI:

• Korelacja może służyć do wyznaczania przesunięcia między sygnałami.

• Sygnały są ortogonalne, gdy ich iloczyn skalarny wynosi zero.