1.Klasyfikacja układów regulacji automatycznej.

Układy regulacji automatycznej można klasyfikować według różnych kryteriów:

1. Ze względu na cechę ( właściwość) liniowości : liniowe , nieliniowe

- układ liniowy spełnia zasadę superpozycji ; układu liniowe opisane są liniowymi równaniami algebraicznymi , różniczkowymi ( zwyczajnymi lub cząstkowymi ) , różnicowymi , całkowymi itd.

- układ nieliniowy nie spełnia zasady superpozycji ; układy nieliniowe opisane są nieliniowymi równaniami algebraicznymi , różniczkowymi ( zwyczajnymi lub cząstkowymi ) , różnicowymi , całkowymi

2. Ze względu na liczbę wejść i wyjść ( wielkości regulowanych ) :

- jednowymiarowe - układy jednej wielkości regulow. mające tylko jedno wejście i tylko jedno wyjście

- wielowymiarowe - ukł. przynajmniej dwóch wielk. regulow.mające więcej niż jedno wejście i wyjście

3. Ze względu na charakter sygnałów :

- układy ciągłe - układy , w których sygnały przesyłane są w sposób ciągły ; dynamiczne układy ciągłe opisane są równaniami różniczkowymi zwyczajnymi lub cząstkowymi ( liniowymi lub nieliniowymi )

- układy dyskretne - nazywamy układy , w których przynajmniej jeden sygnał ma charakter dyskretny ; dynamiczne układy dyskretne są opisane równaniami różnicowymi liniowymi lub nieliniowymi

4. Ze względu na zadanie jakie mają spełniać :

- układy regulacji stałowartościowej - układy , których wielkość zadająca y₀ (t) ma stałą wartość ( y₀ (t) = const ( np. regulacja poziomu cieczy w zbiorniku )

- układy regulacji programowej - układu , których wielkość zadająca y_o (t) jest znaną z góry funkcją czasu ( y_o (t) zmienia się według znanego z góry programu )

- układy regulacji nadążnej - układy , których wielkość zadająca y_o(t) nie jest znaną z góry funkcją czasu ,ale zależy od zjawisk występujących na zewnątrz układu ; w układzie nadążnym wielkość regulowana y(t) nadąża za zmianami y_o (t)

- układy regulacji ekstremalnej - układy , w których wielkości regulowane przyjmują wartości ekstremalne ; regulację ekstremalną stosuje się do obiektów o charakterystykach statycznych ekstremalnych , tzn. będących krzywymi mającymi maksima lub minima

5. Ze względu na zdolność do samoczynnego dopasowywania parametrów i charakterystyk do zmieniających się właściwości obiektów i zakłóceń :

- układy zwykłe ( nie adaptacyjne ) -układy nie mające zdolności do samoczynnego dopasowywania parametrów i charakterystyka do zmieniających się właściwości obiektów i zakłóceń

- układy adaptacyjne - mają powyższą zdolność

6. Ze względu na kryterium jakości ( dobroci ) :

- układy nieoptymalne - układy które nie zapewniają ekstremalnej wartości wskaźnika jakości Q

- układy optymalne - układy zapewniające ekstremalną ( maksymalna lub minimalna ) wartość wskaźnika jakości Q

schemat blokowy ↓ Regulacja w układzie otartym.

u (t) urządzen. m (t) obiekt y(t) u(t) - wielkość zadana ; y(t) - wielkość regulowana

sterujace m (t) - wielkość sterująca ( regulująca)

y(t) ≡ u(t) ( utrzymanie wielkości reg. na poziomie przez wielkość zadaną )

urządz. ster → u(t) → m(t) ; obiekt → m(t) → y(t) ≡ u(t)

urządz. ster. - dobrane na zasadzie odwrotności do obiektu ( nieuniwersalne)

Wady : zakłócenia w układzie ( niedokładne działanie ) , zmienne obciążenie ( efekt ≠ zamiar )

Wniosek : układy regulacji otwartej są bardzo rzadko stosowane

schemat blokowy ↓ Regulacja w układzie zamkniętym.

u(t) + e(t) urządz. m (t) obiekt y(t) tor główny

ster. tor sprzężenia zwrotnego

tor główny → u(t) → y(t) ; tor sprzężenia zwrotnego → y(t) → wej. ukł.

Cel regulacji w układzie zamkniętym - regulacja automatyczna e(t) = u(t) - y(t) = 0

Nie posiada wad regulacji układu otwartego - powszechnie stosowany

2. Metody opisu układu liniowego ciągłego w dziedzinie czasu i częstotliwości .

1. Metody w dziedzinie czasu :

a) Równania różniczkowe

↑-------------------------- f (t) --------------------------↑

b) Odpowiedzi impulsowe

w(t) - odpowiedź impulsowa układu ( funkcja wagi , Diraca )

δ(t) w(t) (we) δ (t) → w(t) (wy) ⇒ δ( t + τ ) → w( t + τ ) ⇒

u(t) y(t) ⇒ u(τ) δ( t - τ ) → u (τ ) w( t - τ ) ⇒ ⇒

↑całka splotu

τ ≥ 0 ; t-τ ≥ 0 ⇒ τ ≤ t wówczas

c) Zmienne stanu

ponieważ x₁ = y ;

zatem
⇒

⇒

[X] = [A] ⋅ [X] + [B] ⋅ [U]→ równanie stanu ; [Y] = [C] ⋅ [X] + [D] ⋅ [U]→ równanie wyjscia

Standardowy schemat blokowy w zmiennych stanu . ↓

2. Metody w dziedzinie częstotliwości :

a) Transformata Fouriera

b) Transformata Laplace'a

3. Transmitancja operatorowa i jej związek z odpowiedzią impulsową układu.

Schemat blokowy jednowymiarowego układu liniowego Niech dany będzie jednowymiarowy układ

liniowy stacjonarny o wymuszeniu u = u(t) i u(t) G( s ) y(t) odpowiedzi y = y(t) . Oznaczmy symbolem

Y(s) U(s) transformatę Laplace'a wymuszenia u(t) , a symbolem Y(s) -transformatę odpowiedzi y(t) .

Transmitancja operatorową G(s) jednowymiarowego układu liniowego stacjonarnego nazywać będziemy wielkość określoną jako stosunek transformaty odpowiedzi Y(s) do transformaty wymuszenia U(s) tego układu przy zerowych warunkach początkowych . G(s) = Y(s) / U(s) . Transmitancja operatorowa jest wielkością zespoloną zależną od parametrów układu i zmiennej zespolonej s. Dla układów liniowych stacjonarnych opisanych równaniami różniczkowymi liniowymi o stałych współczynnikach transmitancja operatorowa jest funkcją wymierną zmiennej s ( tj. ilorazem dwóch wielomianów ) o postaci : G(s) = L(s) / M(s) przy czym

;
; n ≥ m.

Pierwiastki L(s) = 0 nazywamy zerami , a pierwiastki M.(s) = 0 - biegunami transmitancji operatorowej

Transmitancja operatorową G_{i j} (s) między i-tym wyjściem i j-tym wejściem wielowymiarowego układu liniowego stacjonarnego nazywać będziemy wielkość określoną jako stosunek transformaty i-tej odpowiedzi Y_i (s) do transformaty j-tego wymuszenia U_j (s) przy założeniu , że warunki początkowe i wszystkie wymuszenia z wyjątkiem j-tego są równe zeru . G_{i j} (s) = Y_i (s) / U_j (s) dla i = 1, 2 , … ,q

J = 1,2, … , p

W przypadku gdy na rozpatrywany układ działają jednocześnie wszystkie wymuszenia , i-ta odpowiedź jest sumą odpowiedzi wywołanych poszczególnymi wymuszeniami .Wówczas można napisać :

dla i = 1,2, … , q

Funkcja impulsowa ( funkcja wagi , Diraca ) δ(t) - przedstawia nieskończenie wielki impuls działający w nieskończenie krótkim czasie . Odpowiedź impulsową nazywamy odpowiedź układu liniowego na wymuszenie o postaci funkcji impulsowej δ(t) przy zerowych warunkach początkowych

Y(s) = G(s) ⋅X(s) ; sygnał wejściowy x(t) = δ(t) wówczas X(s) = ζ{ δ(t) } = 1 ⇒ X(s) = 1

Zatem : Y(s) = G(s) ⋅ X(s) = G(s) ; y(t) = ζ ^{- 1} { G(s ) } - odpowiedź impulsowa

Przykład . Obliczyć odpowiedź impulsową układu o transmitancji: G(s) = ( ks ) / ( 1 + sτ)

Ponieważ (ks) / ( 1+ sτ ) = k/τ - (k/τ) ⋅ [ 1 / ( 1+sτ) ] zatem

y (t) = ( k/τ ) ⋅ ζ^{- 1} {1} - (k/τ) ⋅ ζ^-1 { 1/ (1+sτ) } ponieważ ζ { δ(t) } = 1 czyli ζ^{- 1}{1} = δ(t) mamy :

4. Metody oceny i wskaźniki jakości regulacji w dziedzinie czasu.

Jakość pracy układu regulacji automatycznej jest określona wielkością uchybu regulacji w czasie całego okresu pracy układu . Jakość ( dobroć) układów lub procesów regulacji ocenia się za pomocą odpowiednio dobranych kryteriów ( wskaźników jakości ) . Kryterium jakości powinno być tak dobrane , aby możliwie dobrze wyrażało wszystkie wymagania technol. , ekonomiczne i inne stawiane układowi .

Kryteria jakości regulacji : 1) kryteria zapasu stabilności , 2) rozkładu pierwiastków równania charakterystycznego , 3) czasowe , 4) częstotliwościowe , 5) całkowe

5. Metody graficznej prezentacji transmitancji widmowej układu .

Transmitancją widmową G(jω) liniowego układu stacjonarnego nazywać będziemy wielkość określona jako stosunek wartości zespolonej składowej wymuszonej odpowiedzi Y(jω) wywołanej wymuszeniem sinusoidalnym do wartości zespolonej tego wymuszenia U (jω). Czyli G(jω) = Y(jω ) / U(jω) . Transmitancja widmowa jest wielkością zespolona zależną od parametrów układu i pulsacji wymuszenia ω .

G(jω) = P(ω) + jQ(ω) przy czym P(ω) = Re [G(jω) ] ; Q(ω) = Im [ G(jω) ]

Analiza układu w dziedzinie częstotliwości

u(t) = U_m sin (ωt + α ) ; y(t) = Y_m. sin ( ωt + α + ϕ ) ;

ω = 2πf = var ; Y_m. = f₁ (ω) = var ; ϕ = f₂ (ω) = var

Y_m. / U_m. = f₁ ( ω ) = G(jω)  ; U = U_m. ⋅ e ^jα ; Y = Y_m. ⋅ e ^{j ( α + ϕ )}

G(jω) = Y / U = ( Y_m. ⋅ e ^{j ( α + ϕ )} ) / ( U_m. ⋅ e ^{j α} )

G(jω) - transmitancja widmowa

G(jω) = [ Y_m. (ω) / U_m (ω) ] ⋅ e ^{j ϕ ( ω )}

G(jω)  = Y_m (ω) / U_m (ω) - ch - ka modułu ( amplitudy )

ϕ (ω) = arg G(jω) - ch - ka fazy

Ch - ka modułu : G(jω)  _{[ dB]} = 20 log G(jω) = 20 log (Y_m. / U_m. ) ; G(jω) = G(s) _{s = jω}

G (jω) =  G (jω)  e ^{j arg G ( jω )} = Re { G(jω) } + j Im {G(jω) }

6. Zasady przybliżonej prezentacji transmitancji widmowej układu ( charakterystyki logarytmiczne modułu i fazy )

7. Elementy rzędu I-go -opis w dziedzinie czasu i częstotliwości.

,

element rzędu 0 → (1) element proporcjonalny [ a₁ , a₂ , b₁ = 0 ]

element rzędu 1 → (2) element inercyjny [ a₂ , b₁ = 0 ]

element rzędu 1 → (3) element różniczkujący idealny [ a₂ , a₁ , b₀ = 0 ]

element rzędu 1 → (4) element różniczkujący rzeczywisty [ a₂ = 0 , b₀ = 0 ]

element rzędu 1 → (5) element całkujący idealny [ a₂ = 0 , a₀ , b₁ = 0 ]

Element proporcjonalny (1).

a₀ ⋅y = b₀ ⋅u ⇒ y = ( b₀ ⋅ u ) / a₀ = k ⋅ u ; k - współ. proporcjonalności

u(t) = δ(t) → y(t) = k ⋅ δ(t)

u(t) = 1(t) → y(t) = k ⋅ 1(t)

G(s) = k ; G(jω ) = k

20 log G = 20 log k

Element inercyjny (2)

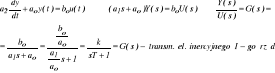
Ch - ka w dziedzinie czasu :

Ch-ka w dziedzinie częstotliwości :

G(jω) = k / ( jωT+1) ⇒ L(ω) = 20 log  G(jω) =

= 20 log [ k / ( 1+ ( ωT )² ) ^0,5 = 20 log k - 20 log [ (ωT)² +1] ^0,5

ωT << 1 → L(ω) = 20 log k

ωT >> 1 → L(ω) = 20 log k - 20 log ωT

ωT = 1 → nachylenie - 20 dB / dekadę

Element różniczkujący idealny (3). ciąg dalszy →

Ch-ka w dziedzinie czasu :

(d / dt ) ⋅ { δ(t) } - odp. Impulsowa ;

Y₁( t ) = (1/s ) ⋅ k⋅ s = k ⇒

Y₁(s) = k ⋅ δ(t) - odp. jednostkowa

Ch - ka w dziedzinie częstotliwości :

G(jω) = k ⋅ jω ; G(jω) = k ⋅ ω

L(ω) = 20 log ( k⋅ ω ) = 20 log k +20 log ω

arg G(jω) = + π/2

Element różniczkujący rzeczywisty (4) .

; Ch -ka w dzie. czasu :

Ch -ka w dziedzinie częstotliwości :

G(jω) = (k ⋅ jω) / (1 + jωT) ; L(ω) = 20 log kω - 20 log [ 1+ (ωT)² ] ^0,5 ; arg G(jω) = ( π/2 ) - arctg(ωT)

Element całkujący idealny (5) .

Ch-ka w dziedzinie czasu : y_o(t) = k ⋅ 1(t) ; y₁(t) = ζ^-1 { (1/s ) ⋅ ( k / s ) } = k ⋅ t ⋅ 1 (t)

Ch - ka w dziedzinie częstotliwości : G(jω) = k / jω

L(ω) = 20 log ( k/ω ) = 20 log k - 20 log ω

8. Elementy rzędu II-go - charakterystyki w dziedzinie czasu i częstotliwości.

(elementy : całkujący rzeczywisty , inercyjny rzędu II-go i oscylacyjny )

element rzędu 2 → (6) element całkujący rzeczywisty [ a₀ , b₁ = 0 ]

element rzędu 2 → (7) element inercyjny ; s₁ , s₂ - rzeczywiste ; b₁ = 0

element rzędu 2 → (8) element oscylacyjny ; s₁ , s₂ - zespolone sprzężone ; b₁ = 0

Element całkujący rzeczywisty (6) .

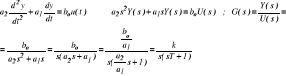
Ch - ka w dziedzinie czasu :

→

→

Ch - ka w dziedzinie częstotliwości : G(jω) = k / [ jω(1 + jωT) ] ; Ch - ka amplitudowo - fazowa ↓

L(ω) = 20 log (k/ω) - 20 log [ 1 + (ωT)² ] ^0,5

arg G(jω) = - (π/2) - arctg ω

G(jω) = k / [ jω ( 1+jωT ) ] = -jk / [ ω(1+jωT )] =

= [ -jk(1-jωT) ] / [ ω(1+(ωT)² )] =

= - kωT / [ ω(1+(ωT)² )] = jk / [ ω(1+(ωT)² )]

Element inercyjny II- go rzędu (7) .

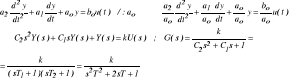
Ch - ka w dziedzinie czasu : gdy Cs² + Cs +1 = 0

Dla C₁² - 4 ⋅ C₂ > 0 → dwa bieguny rzeczywiste ;

Dla C₁² - 4 ⋅ C₂ < 0 → dwa bieguny zespolone ;

Ch - ka w dziedzinie częstotliwości : Ch - ka logarytmiczna ↓ ( k = 10 , T₁ = 1 ; T₂ = 0,1)

G(jω) = k / [ (1+ jωT₁ ) ( 1+ jωT₂ ) ]

L(ω) = 20 log k - 20 log [ 1+(ωT₁ )² ] ^0,5 -

- 20 log [ 1+(ωT₂ )² ] ^0,5

Element oscylacyjny ( 8) .

;

cosϕ = n ; tg ϕ = [ 1 - n² ] ^0,5 / n ; n - współczynnik tłumienia ( 0 ÷1 ) ; Ch - ka w dziedzinie czasu :

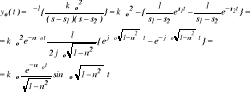
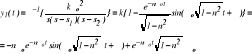
- względna wartość przeregulowania ; t_u = ln ( 2% ) / [ nω₀ ] - czas ustalenia

Ch - ka w dziedzinie częstotliwości :

G (jω) = kω₀² / [ ω₀² - ω² - j 2 n ω₀ ⋅ ω ] = k / [ 1 - ( ω / ω₀ ) ² + j 2 n ( ω / ω₀ ) ] = k / [1-x² + 2 j n x ] ] X]XXxxxxxhg

= = k / [ ( 1 - x² ) + (2 nx)² ]

d/dx { ( 1 - x² ) + (2 nx)² } = 0 ⇒ 2( 1 - x ) ⋅ (- 2x ) + 8 n² x = 0 ⇒ - 4x { 1-x² - 2n² } = 0 ;

x = (1- 2n² ) ^0,5 ; ω_r = ω₀ ⋅ ( 1 - 2n ² ) ^0,5 ; G(jω) = k / [ 1 - (ω / ω₀ ) ² + 4n² ⋅ ( ω / ω₀ )² ] ^0,5

ω << ω₀ ⇒ k ; ω >> ω₀ ⇒ k / ( ω / ω₀ )²

Przy rezonansie charakterystyki logarytmiczne są mało dokładne .( zwłaszcza gdy n = ( 0,7 ÷ 1 )

9. Algebra schematów blokowych układów liniowych ciągłych ( transmitancje zastępcze dla różnych typów połączeń , przesuwanie położenia węzłów sumacyjnych i zaczepowych ) .

Połączenie szeregowe : G (s) = Y(s) / U(s) = G1(s) ⋅ G2 (s)	Przenoszenie węzła sumacyjnego z wejścia na wyjście :
Połączenie równoległe : G (s) = Y(s) / U(s) = G1(s) + G2 (s)	Przenoszenie węzła sumacyjnego z wyjścia na wejście :
Układ ze sprzężeniem zwrotnym : G(s) = G1 (s) / [ 1 ± G1 (s) ⋅ G 2 (s) ]	Zamiana miejscami węzła sumacyjnego z węzłem zaczepowym przy przenoszeniu węzła sumacyjnego w kierunku: a) zgodnym z przepływem sygnału w gałęzi b) przeciwnym do kierunku przepływu sygnału w gałęzi
Przenoszenie węzła zaczepowego z wyjścia na wejście :
Przenoszenie węzła zaczepowego z wejścia na wyjście :

10. Uchyby statyczne w układach ciągłych - definicje , określanie uchybów w oparciu o transmitancję operatorową układu , minimalizacja .

Uchyby ustalone E(s) = U(s) / [ 1+ G(s) ] Schemat blokowy ↓

lim e(t) = e_u

t → ∞

1. Uchyb ustalony statyczny : u(t) = 1(t)

(położenia )

2. Uchyb ustalony prędkościowy : u(t) = t ⋅ 1(t)

3. Uchyb ustalony przyśpieszenia : u(t) = ( t² / 2 ) ⋅ 1(t)

lim e(t) = lim sE(s)

t→ ∞ s→ 0

dla 1) e_US = lim s ⋅ (1 / s ) ⋅ [ 1 / (1 + G(s) ) ] = 1 / ( 1 + lim G(s) ) ; k_US = lim G(s)

s→0 s→0 s→0

dla 2) e_UV = lim s ⋅ (1 / s² ) ⋅ [ 1 / (1 + G(s) ) ] = 1 / ( lim s ⋅ G(s) ) ; k_UV = lim s ⋅ G(s)

s→0 s→0 s→0

dla 3) e_Ua = lim s ⋅ (1 / s ³ ) ⋅ [ 1 / (1 + G(s) ) ] = 1 / ( lim s² ⋅ G(s) ) ; k_Ua = lim s² ⋅ G(s)

s→0 s→0 s→0

G(s) = ( 1 / s ^m. ) ⋅ G^* (s) ; m. - klasa astatyzmu układu

m =	eUS	kUS	eUV	kUV	eUa	kUa
0	1 / (1+ k)	k	∞	0	∞	0
1	0	∞	1 / k	k	∞	0
2	0	∞	0	∞	1 / k	k
3	0	∞	0	∞	0	∞

11. Stabilność liniowych ciągłych URA - definicje , podstawowy warunek stabilności , kryteria analityczne ( Routha , Hurwitza ) .

Układ stabilny jest to układ , w którym przy zerowym sygnale wymuszającym U= 0 oraz dowolnych wartościach początkowych ma stan przejściowy , który zdąża do skończonej wartości przy t → ∞ .

Układ jest stabilny asymptotycznie gdy przy zerowych warunkach asymptotycznych ( U = 0 ) , dowolnych wartościach początkowych , stan przejściowy zdąża do zera przy t → ∞ .

Układ o danej transmitancji G(s) jest stabilny asymptotycznie jeśli jego wszystkie bieguny będą położone w lewej części płaszczyzny pierwiastków ( tzn. mają ujemną część rzeczywistą ).

Badanie stabilności układów ciągłych liniowych sprowadza się do badania położenia pierwiastków równania charakterystycznego M (s) = a _n s ⁿ + … + a ₁ s + a₀ = 0 na płaszczyźnie zmiennej zespolonej s .

Kryterium stabilności Routha

Równanie M (s) = a _n s ⁿ + … + a ₁ s + a₀ = 0 ( przy czym G(s) = L(s) / M (s) ) ma wszystkie pierwiastki w lewej półpłaszczyźnie płaszczyzny zmiennej zespolonej s , jeżeli :

1. wszystkie współczynniki a_n , … , a ₁ , a₀ są różne od zera i mają ten sam znak

2. wszystkie współczynniki pierwszej ( lewej skrajnej ) kolumny tablicy

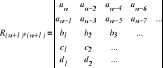
przy czym

;
;
;

;
mają ten sam znak . Gdy współczynniki I kolumny wyznacznika nie są tego samego znaku to układ jest niestabilny , a liczba zmian znaków współczynników pierwszej kolumny tablicy równa się liczbie pierwiastków z dodatnią częścią rzeczywistą , to jest liczbie pierwiastków w prawej półpłaszczyźnie płaszczyzny zmiennej zespolonej s .

Kryterium stabilności Hurwitza.

Równanie M (s) = a _n s ⁿ + … + a ₁ s + a₀ = 0 ( przy czym G(s) = L(s) / M (s) ) o współczynniku a_n > 0 ma wszystkie pierwiastki w lewej półpłaszczyźnie płaszczyzny zmiennej zespolonej s , wtedy i tylko wtedy gdy :

Δ₁ = a _{n -1 ­} > 0 ;
;
ciąg dalszy →

Kryterium stabilności Hurwitza - ciąg dalszy .

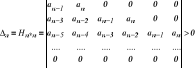
Warunkiem koniecznym ( ale nie dostatecznym ) położenia wszystkich pierwiastków równania w lewej półpłaszczyźnie jest a _i > 0 dla i = 0,1,…, n - 1

12. Częstotliwościowe metody badania stabilności układów liniowych ciągłych

- kryteria Michajłowa , Nyquista i logarytmiczne .

Kryterium Michajłowa.

G(s) - transm. układu otwartego ; K(s) - transm . układu zamkniętego Wykresik ↓

G(s) ; K(s) = L(s) / [ a _n s ⁿ + a _{n - 1} s ^{n - 1} + … + a ₁ s + a₀ ]

M(s) = a _n ( s - s ₁ ) (s - s ₂ ) ⋅ … ⋅ (s - s _{n - 1} ) ( s - s _n )

M (jω) = a _n ( jω - s₁ ) ( jω - s₂ ) …

Badamy zmianę argumentów : Δarg ( jω - s _k ) = + π gdy - ∞ < ω < ∞ ;

Δarg ( jω - s _m ) = - π gdy - ∞ < ω < ∞

Δ arg M (jω) = n ⋅ π ; - ∞ < ω < ∞ oraz Δ arg M (jω) = n ⋅ ( π / 2 ) ; 0 < ω < ∞ ⇒ warunek statyczności asymptotycznej

k - pierwiastków w proj. płaszczyźnie ; n-k - pierwiastków w danej półpłaszczyźnie

Δ arg M(jω) = (n - k) ⋅ π - kπ = n ⋅ π - 2kπ = Ψ₁ ; - ∞ < ω < ∞

Δ arg M(jω) = n ⋅ ( π / 2 ) - kπ = Ψ₂ ; 0 < ω < ∞

Kryterium Nyquista.

Kryterium to pozwala badać stabilność liniowego układu zamkniętego na podstawie charakterystyki amplitudowo - fazowej układu otwartego, którą można określić doświadczalnie .

Zamknięty układ regulacji jest stabilny ⇒ zmiana argumentów wyrażenia [ 1 + G _1,2 ( jω) ] przy zmianie pulsacji od - ∞ do + ∞ spełnia warunek : 2π ⋅ Np + π ⋅ Np₁ ⇐⇒Δ arg [ 1 + G _1,2 ( jω) ] _{- ∞}^{+ ∞} = = 2π ⋅ Np + π ⋅ Np ₁ ; przy czym :

Np - ilość biegunów układu otwartego w prawej półpłaszczyźnie Re [ s _k ] > 0

Np ₁ - ilość biegunów układu otwartego leżących na osi urojonej Re [ s _k ] = 0

Układ jest stabilny ⇐⇒ Δ arg [ 1 + G _1,2 ( jω) ] _{- ∞}^{+ ∞} = π ⋅ Np + ( π / 2 ) ⋅ Np ₁

Stosowanie kryterium Nyquista

- wykreślanie ch - ki amplitudowo - fazowej układu otwartego G_{1 ,2} (jω)

- G_1,2 (jω) = G _1,2 (s) _{s = jω} ( wykreślamy analitycznie )

- zdjęcie doświadczalne ch - ki na „żywym” obiekcie

- sprecyzowanie wartości Np , Np ₁

- sprecyzowanie warunku stabilności ; - sprawdzenie warunku stabilności ciąg dalszy →

Wersje uproszczone .

- kryterium lewej strony

- kryterium logarytmiczne

stosowane gdy układ otwarty jest minimalno - fazowy tzn. G_1,2 (s) nie posiada ani zer ani biegunów w prawej półpłaszczyźnie ⇒ Np = 0

Kryterium lewej strony

Zamknięty układ URA jest stabilny ⇐⇒ gdy wędrując po ch - ce amp. - fazowej układu otwartego pozostawiamy punkt ( -1 , j0 ) po lewej stronie .

Kryterium logarytmiczne.

1. bazuje na ch - kach logarytmicznych amplitudy. i fazy

2. bazuje na ch - ce logarytmicznej amplitudowo - fazowej

ad. 1. Układ zamknięty jest stabilny jeżeli w zakresie pulsacji dla których logaryt. ch - ka modułu jest dodatnia  G_1,2 (jω) _dB > 0 . Charakterystyka fazy osiąga wartość - π parzystą ilość razy .

ad.2. Układ zamknięty jest stabilny ⇐⇒ kiedy wędrując po ch - ce logarytmicznej amplitudowo - fazowej układu otwartego punkt ( -π ; 0 dB ) zostanie po prawej stronie .

14. Zapas wzmocnienia i zapas fazy - definicje , interpretacja graficzna .

Zapas fazy i zapas wzmocnienia dotyczy układów stabilnych . Im większy zapas fazy , tym większy zapas wzmocnienia i tym samym układ bardziej stabilny .

Zapas wzmocnienia	Zapas fazy .
- ile krotnie można zwiększyć wzmocnienie by układ został stabilny Δk = 1 / [ G1,2 (jω) ω 1 ] ( jednostki względne ) ω1 : arg G12 (jω) = -π Δk = 1 /x ΔkdB = -  G12 (jω)  ω1 [ dB] Wykres ↓	- wartość fazy o którą można zmienić argument by układ był jeszcze stabilny przy stałym wzmocnieniu ( module ) Δϕ = π + arg G12 (jω) ω2 :  G12 ( jω )  = 1  G12 ( jω ) dB = 0 Wykres ↓

---