Natężenie pola elektrycznego.
Każdemu punktowi pola elektrostatycznego przyporządkowany jest wektor natężenia pola E, wektor indukcji elektrostatycznej D oraz potencjał elektryczny V, który jest wielkością skalarną.
Jeżeli w pewnym punkcie pola elektrostatycznego, wytworzonego przez ładunek Q, umieścimy niewielki ładunek próbny q, to znajdzie się on pod działaniem siły Coulomba, określonej przez zależność (2.1) ![]()
Wartość siły F jest różna w różnych punktach pola, a jej stosunek do wartości ładunku próbnego q jest dla każdego punktu wielkością charakterystyczną i stanowi miarę natężenia pola elektrycznego E w tym punkcie (rys. 2.1)
Napięcie elektryczne.
Napięcie elektryczne między dwoma dowolnymi punktami A i B w polu elektrycznym jest równe stosunkowi pracy przy przenoszeniu małego dodatniego ładunku próbnego q z punktu A do punktu B, do tego ładunku
![]()
Polem elektrostatycznym nazywamy pole elektryczne wytworzone przez ładunki nieruchome i niezmienne w czasie. Określenie jednostki napięcia na podstawie wzoru (2.9) nie jest stosowane ze względu na trudności pomiaru małego ładunku próbnego w stanie statycznym, jak też pomiaru wykonanej pracy. Jednostkę napięcia określamy na podstawie pracy lub mocy mierzonej przy przepływie prądu elektrycznego przez przewód. Prąd stały o wartości jednego ampera przenosi w ciągu jednej sekundy ładunek równy jednemu kulombowi. Jeżeli tracona przy tym moc jest równa jednemu watowi, to napięcie jest równe jednemu woltowi ![]()
Potencjał elektryczny.
Aby wyznaczyć potencjał w dowolnym punkcie A pola elektrycznego (rys. 2.2), umieszczamy w tym punkcie ładunek próbny q i przesuwamy go do nieskończoności (∞). W miarę oddalania ładunku q siła F maleje odwrotnie proporcjonalnie do kwadratu odległości, tak, że wykonana praca ma wartość skończoną mimo dużej drogi przesunięcia.
Potencjał w dowolnym punkcie pola jest równy stosunkowi pracy wykonanej przy przesunięciu dodatniego ładunku próbnego, z danego punktu pola do nieskończoności, do tego ładunku.
Potencjał oznaczamy literą V z ewentualnym dodaniem wskaźnika, do którego ten potencjał się odnosi, np. VA oznacza potencjał w punkcie A ![]()
Gdy punkt A znajduje się na przewodniku, wówczas VA jest potencjałem tego przewodnika.
Potencjał jest dodatni, gdy praca WA jest wykonana kosztem sił pola, np. w polu elektrycznym wytworzonym przez dodatni ładunek Q
Linie pola elektrycznego.
Powierzchnie ekwipoten-cjalne.
Praca w polu elektrycznym.
W obwodzie elektrycznym przesuniecie elementarnego ładunku dodatniego +dq z punktu A o potencjale VA, do punktu B o potencjale VB niższym od potencjału punktu A, wymaga wykonania pracy ![]()
Uwzględniając zależność między ładunkiem elektrycznym, prądem oraz czasem: ![]()
otrzymuje się ![]()
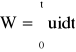
.Dla prądu stałego u = U = const oraz i = I = const, a więc ![]()
Jednostką pracy jest dżul (J).
Przewodniki I rodzaju.
Przewodniki II rodzaju.
Natężenie prądu elektrycznego.
Prądem elektrycznym (natężeniem prądu) nazywamy stosunek ładunku przepływającego przez przekrój przewodnika do czasu (ta sama nazwa prąd jest stosowana do określania zarówno zjawiska, jak i wielkości fizycznej określającej to zjawisko)
![]()
Prąd elektryczny ma określony zwrot (kierunek). Za kierunek przepływu prądu przyjęto umownie kierunek od bieguna dodatniego (miejsca o potencjale wyższym) do bieguna ujemnego (miejsca o potencjale niższym). Prąd elektryczny traktuje się jako pozorny przepływ ładunków dodatnich, bo w rzeczywistości prąd elektryczny w przewodnikach jest ruchem ładunków ujemnych (elektronów) od bieguna ujemnego do dodatniego, chociaż w gazach i cieczach może istnieć równocześnie przepływ jonów naładowanych dodatnio w kierunku przeciwnym. W każdym zamkniętym obwodzie elektrycznym rozróżnia się dwie części: zewnętrzną, w której prąd przepływa od dodatniego bieguna źródła, przez przewodnik, do bieguna ujemnego, oraz wewnętrzną - wewnątrz źródła prądu, w której przepływ odbywa się od bieguna ujemnego do dodatniego. W części zewnętrznej obwodu jest włączany odbiornik energii. Jeżeli wartość prądu oraz zwrot są stałe w funkcji czasu, to
![]()
Prąd taki nosi nazwę prądu stałego. Jednostką prądu elektrycznego jest amper (A). Jest to natężenie takiego prądu, który w czasie 1 sekundy przenosi ładunek 1 kulomba
![]()
Amper jest natężeniem prądu elektrycznego nieulegającego żadnym zmianom, który przepływając w dwóch równoległych przewodach prostoliniowych o długości nieskończonej i o przekroju kołowym znikomo małym, umieszczonych w próżni o odległości 1 m od siebie, wytwarza między tymi przewodami siłę, równą 2ּ10-7 N na każdy metr długości przewodu.
Prawo Ohma w postaci całkowej.
Gęstość prądu elektrycznego.
Gęstością prądu nazywamy wektor, równy liczbowo stosunkowi prądu di do przekroju dsn poprzecznego (normalnego) do kierunku ruchu ładunków
![]()
Jest to liczba ładunków, które przeszły w czasie dt przez element powierzchni dsn,, prostopadłej do kierunku ruchu ładunków. Jednostką gęstości prądu jest amper na metr kwadratowy (A/m2). Prąd elektryczny przepływający przez dowolną powierzchnię jest równy loczynowi strumienia wektora gęstości prądu przez tę powierzchnię ![]()
Prawo Ohma w postaci różniczkowej.
Rezystancja i konduktancja.
W stałej temperaturze (υ = const) i przy stałym ciśnieniu (p = const), rezystancja przewodnika o stałym przekroju, wykonanego z materiału jednorodnego, jest wprost proporcjonalna do długości przewodnika i odwrotnie proporcjonalna do jego przekroju ![]()
Współczynnik proporcjonalności ρ, którego wartość zależy od rodzaju materiału przewodu, nosi nazwę rezystywności (oporu właściwego).
Jednostką rezystywności jest omometr (Ω·m). Ze względów praktycznych stosuje się niekiedy jako jednostkę rezystywności om razy milimetr kwadratowy na metr (Ω·mm2/m): ![]()
Odwrotnością rezystywności jest konduktywność (przewodność właściwa) ![]()
Jednostką konduktywności jest siemens na metr (S/m). Ze względów praktycznych (przewody mają przekroje od kilku do kilkudziesięciu milimetrów kwadratowych, a długości - rzędu dziesiątków metrów) stosuje się również jako jednostkę siemens razy metr na milimetr kwadratowy (Sm/mm2) ![]()
Zależność rezystancji od temperatury.
Ze zmianą temperatury ulega zmianie rezystywność materiałów. Rezystywność przewodników rośnie prawie liniowo ze wzrostem temperatury. Rezystywność półprzewodników maleje ze wzrostem temperatury krzywoliniowo. W elektrotechnice przyjęto podawać wartości rezystywności przy temperaturze 20 oC. Zależność rezystancji elementów metalowych od temperatury w zakresie temperatur od - 100 oC do +200 oC można przedstawić w postaci wzoru ![]()
gdzie: υ2 - υ1 - przyrost temperatury, K; R1, R2 - rezystancje przy temperaturach υ1 i υ2, Ω; α - współczynnik temperaturowy rezystancji, 1/K.
Współczynnik temperaturowy rezystancji jest to względny przyrost rezystancji przy wzroście temperatury o 1 K. Współczynnik temperaturowy rezystancji jest zależny od temperatury. W elektrotechnice przyjmuje się jego wartość odpowiadającą temperaturze 20 oC. Błąd spowodowany tym założeniem jest na ogół pomijalnie mały. Wówczas zależność (1.14) ma postać ![]()
Rezystancja lub konduktancja odcinka przewodu.
Prawo Coulomba.
Prawo Coulomba określa siłę wzajemnego oddziaływania ładunków punktowych, tj. przyciągania się ładunków różnoimiennych i odpychania jednoimiennych![]()
przy czym: F - siła oddziaływania, N;
Q1, Q2 - ładunki, C;
R - odległość między ładunkami, m;
ε - przenikalność elektryczna bezwzględna środowiska, F/m.
Indukcja elektryczna.
Indukcja elektryczna D w danym punkcie jest zależna od wektora natężenia pola E ![]()
![]()
Indukcja elektryczna nie zależy od właściwości elektrycznych środowiska. Na przykład w polu ładunku punktowego indukcja ![]()
zależy od ładunku wytwarzającego pole oraz od powierzchni S kuli o promieniu r ![]()
W polu ładunku punktowego Q powierzchnie kuliste, w których środku mieści się ładunek, są miejscami geometrycznymi punktów, w których indukcja D jest stała. Na powierzchniach tych stałe jest także natężenie pola E, o ile środowisko jest jednorodne i izotropowe. Jednostką indukcji elektrycznej D jest kulomb na metr kwadratowy (C/m2). Indukcja elektrostatyczna na powierzchni kuli jest miarą powierzchniowej gęstości ładunku. Gęstość ładunku zależy od kształtu powierzchni przewodnika. Na przewodnikach kulistych jest ona jednakowa w każdym punkcie powierzchni, natomiast na przewodnikach o różnej krzywiźnie jest większa tam, gdzie mniejszy jest promień krzywizny.
Strumień elektryczny.
Twierdzenie Gaussa.
Przewodniki w polu elektrostatycznym.
Przewodniki charakteryzują się małą rezystywnością (1,6·10-8 … 10-4 Ω·m). Należą do nich metale i węgiel, w których przepływ prądu polega na ruchu elektronów swobodnych, czyli przewodnictwie elektronowym (w metalach liczba elektronów swobodnych wynosi ok. 1023 na cm3), oraz roztwory, w których przepływ prądu polega na ruchu dodatnio i ujemnie naładowanych jonów, czyli przewodnictwie jonowym.
Polaryzacja dielektryków i przenikalność elektryczna.
Dielektryki różnią się od przewodników tym, że prawie nie zawierają ładunków swobodnych. Dodatnie i ujemne ładunki występują w dielektryku w sposób związany między sobą (rys. 2.11). Przy obecności pola elektrycznego występuje w dielektryku przemieszczenie związanych ładunków, dodatnich w kierunku pola, ujemnych - w kierunku przeciwnym. Zmiana położenia molekuł w dielektryku pod wpływem sił pola elektrycznego nazywa się polaryzacją. Przemieszczenie ładunków jest tym większe, im większe jest natężenie E pola elektrycznego. Przy zmniejszeniu E do zera polaryzacja dielektryka znika.
Prąd przesunięcia dielektrycznego.
Kondensatory i ich układy połączeń.
Pojemność elektryczna lub elastancja kondensatora płaskiego.
![]()
(2.15)
Współczynnik proporcjonalności C nazywa się pojemnością elektryczną. Jest to parametr charakteryzujący kondensator i określający możliwości gromadzenia przez ten kondensator ładunków elektrycznych. Jednostką pojemności elektrycznej jest farad [F]: ![]()
Farad jest jednostką dużą i w praktyce operuje się jednostkami mniejszymi:
1μF = 10-6F, 1nF = 10-9F, 1pF = 10-12F ![]()
Wynika z tego, że pojemność kondensatora zależy od konfiguracji i wymiarów okładzin oraz od przenikalności elektrycznej ε.
Energia pola elektrostatycznego.
W polu elektrycznym istnieje zasób energii, która jest rozłożona w całym obszarze pola.
Energię kondensatora płaskiego można obliczyć, uwzględniając zależności![]()
, ![]()
oraz wzór na natężenie pola elektrycznego w kondensatorze płaskim ![]()
![]()
== Zależność jest słuszna także dla innych rodzajów kondensatorów.
Wytrzymałość elektryczna.
Jeżeli natężenie E pola elektrycznego przekroczy określoną dla danego dielektryka wartość, to siły pola, działające na różnoimienne ładunki w dielektryku, przewyższą siły utrzymujące te ładunki w stanie związanym. Pociąga to za sobą przebicie dielektryka i utratę jego właściwości izolacyjnych. Przebiciu towarzysza wyładowania elektryczne w postaci iskier, huku, świecenia lub snopienia. Najmniejszą wartość natężenia pola elektrycznego, przy którym rozpoczyna się przebicie dielektryka, nazywa się wytrzymałością elektryczną.
Elementy aktywne i pasywne w obwodzie elektrycznym.
Rezystancja statyczna oporników nieliniowych.
Prawa Kirchhoffa.
W żadnym punkcie obwodu prądowego nie może gromadzić się ładunek elektryczny, więc suma prądów dopływających do węzła jest równa sumie prądów wypływających. Przypisując prądom dopływającym wartość +Ik, a wypływającym wartość -Ik, można dla dowolnego węzła, w którym schodzi się n gałęzi napisać równanie ![]()
.Wzór ten wyraża pierwsze prawo Kirchhoffa, czyli „prawo prądów”, mianowicie: algebraiczna suma prądów dopływających do każdego węzła obwodu elektrycznego jest równa zeru.
W przypadku węzła pokazanego na rys. 1.3 jest -I1 + I2 - I3 + I4 - I5 + I6 = 0.
Napięcie, występujące na dowolnej gałęzi (o końcówkach AB) obwodu jest równe różnicy potencjałów na końcach tej gałęzi ![]()
Rozpatrując dowolne oczko obwodu z dowolną liczbą rozgałęzień, oraz przyjmując założenie, że prąd I ma wartość dodatnią jeżeli płynie z punktu M do punktu N, ujemną zaś, jeżeli płynie w kierunku przeciwnym, można utworzyć dla każdej gałęzi obwodu pokazanego na rys. 1.4, wyrażenie analogiczne do ![]()
zaś dla każdego oczka ![]()
Wzór ten wyraża drugie prawo Kirchhoffa, czyli „prawo napięć”; mianowicie: w oczku obwodu elektrycznego algebraiczna suma napięć źródłowych jest równa algebraicznej sumie iloczynów rezystancji i prądów (algebraicznej sumie spadków napięć).
Praca i moc elektryczna elementów obwodu elektrycznego.
Moce pobierane oraz wydawane przez elementy w obwodzie elektrycznym.
Idealne i rzeczywiste źródła napięciowe i prądowe -stan jałowy i stan zwarcia źródła, sprawność źródła.
Dopasowanie odbiornika do rzeczywistego źródła napięciowego.
Dopasowanie odbiornika do rzeczywistego źródła prądowego.
Zamiana rzeczywistego źródła napięciowego na równoważne źródło prądowe, i na odwrót.
Połączenie równoległe rzeczywistych źródeł napięciowych.
Linia zasilająca odbiornik.
Dzielnik napięcia i dzielnik prądu.
Rozszerzenie zakresu pomiarowego woltomierza.
Rozszerzenie zakresu pomiarowego amperomierza.
Planarność i spójność obwodu elektrycznego.
Dendryty (największe drzewa), węzły niezależne i oczka niezależne obwodu elektrycznego.
Incydencja gałęzi z węzłami oraz oczkami -współczynniki i macierze incydencji: węzłów i gałęzi oraz oczek i gałęzi (zapisanie macierzy incydencji przykładowych obwodów).
Gałąź uogólniona.
Równania równowagi (praw Kirchhoffa).
Zasada superpozycji.
„Przenoszenie" idealnych źródeł napięciowych (należących do gałęzi bezrezystancyjnych) do innych gałęzi obwodu.
„Przenoszenie" idealnych źródeł prądowych (tworzących „pseudogałęzie", tzn. nienależących do gałęzi obwodu) do gałęzi obwodu.
Twierdzenie o kompensacji.
Twierdzenie Thevenina.
Każdy aktywny (zawierający źródła) obwód liniowy rozgałęziony, rozpatrywany od strony dwóch dowolnych zacisków, może być zastąpiony równoważnym rzeczywistym źródłem napięcia (rys. 1.23). Wartość napięcia źródłowego Uo tego źródła jest równa napięciu między otwartymi zaciskami rozważanego obwodu; rezystancja wewnętrzna Rw jest równa rezystancji rozważanego obwodu, widzianej od strony zacisków, przy założeniu, że wszystkie idealne źródła napięcia są zwarte, a idealne źródła prądu są w stanie jałowym (stanowią przerwy). Jeżeli do pary zacisków obwodu liniowego (rys. 1.24), między którymi występuje napięcie Uo, zostanie przyłączona rezystancja R, to prąd płynący przez tę rezystancję
![]()
Jeżeli natomiast do pary zacisków obwodu liniowego (rys. 1.25), między którymi występuje napięcie Uo, zostanie przyłączona gałąź zawierająca źródło o napięciu źródłowym E i rezystancję R, to prąd płynący przez tę gałąź
![]()
Zastosowanie twierdzenia Thevenina do rozwiązywania obwodów elektrycznych liniowych umożliwia wyznaczenie wartości prądu płynącego w tej gałęzi, bez konieczności ułożenia i rozwiązania określonego układu równań. Rozpatrywana gałąź jest przyłączona do zacisków AB obwodu utworzonego przez wszystkie pozostałe elementy.
Mostek Wheatstone'a.
Działanie pola magnetycznego na „elementy prądowe" - indukcja magnetyczna.
Siłę dF, z jaką pole magnetyczne oddziałuje na nieskończenie mały odcinek dl przewodnika liniowego, przez który przepływa prąd I, zwaną siłą Laplace'a, wyraża równanie
![]()
Siła jest równa iloczynowi wektorowemu dwóch wektorów, z których jeden Idl (zależny od obwodu) ma kierunek przepływającego prądu, drugi zaś B, charakteryzujący pole magnetyczne w danym punkcie (rys. 3.3), ma kierunek zgodny z linią pola. Wektor B nosi nazwę wektora indukcji magnetycznej. Moduł siły ma wartość
![]()
Na obwód zamknięty, w którym płynie prąd I, działa siła![]()
Kierunek działania siły F można ustalić, posługując się regułą lewej dłoni
Jeżeli lewa dłoń jest tak ustawiona, że wektor indukcji magnetycznej jest skierowany prostopadle ku wewnętrznej stronie dłoni, a cztery złączone palce pokrywają się z kierunkiem prądu, to wyprostowany kciuk wskazuje kierunek działania siły mechanicznej.
Jednostką indukcji magnetycznej jest 1 Vּs/m2 = 1 Wb/m2 = 1 T (tesla). Dawniej jednostką indukcji był 1 Gs (gaus), przy czym 1 Gs = 10-4 T.
Strumień magnetyczny.
Strumień wektora indukcji magnetycznej, przenikający przez daną powierzchnie, nazywany strumieniem magnetycznym Φ, wyraża wzór ![]()
Kąt α jest kątem zawartym między normalną do powierzchni elementarnej ds i wektorem indukcji magnetycznej B (rys.3.5).
Jednostką strumienia magnetycznego (powiązaną z jednostką napięcia elektrycznego) jest woltosekunda, zwana także weberem (Wb). Dawniej jednostką strumienia był makswel [1 Mx], przy czym 1 Mx = 10-8 Wb. Strumień magnetyczny przenikający dowolną powierzchnię zamkniętą jest równy zeru ![]()
Pole magnetyczne jest wiec polem bezźródłowym.
Natężenie pola magnetycznego.
Niektóre zjawiska w polu magnetycznym, np. oddziaływanie przewodnika z prądem na igłę magnetyczną, nie zależą od właściwości magnetycznych środowiska. Toteż, w celu opisania pola magnetycznego, wprowadza się wielkość wektorową H, zwana natężeniem pola magnetycznego, niezależną od przenikalności magnetycznej ośrodka. Jednostką natężenia pola magnetycznego jest amper na metr (A/m). Między indukcją magnetyczną i natężeniem pola magnetycznego istnieje zależność ![]()
Przenikalność magnetyczna.
Prawo Biota-Savarta-Laplace'a.
Prawo przepływu.
![]()
Równanie (3.17) jest matematyczną postacią prawa przepływu, które można wyrazić następująco: dla zamkniętego obwodu magnetycznego suma spadków napięć magnetycznych równa się sumie sił magnetomotorycznych działających w tym obwodzie. Ponieważ prąd elektryczny płynie również w obwodzie zamkniętym, więc prawo przepływu wyraża jednocześnie związek prądu elektrycznego z polem magnetycznym.
Jeżeli obwód magnetyczny można podzielić na n odcinków, w których istnieje równomierne pole magnetyczne, to wzór upraszcza się: ![]()
.
Prawo przepływu jest podstawowym prawem, służącym do obliczania obwodów magnetycznych.
Oddziaływanie elektrodynamiczne przewodów z prądem.
Krzywa magnesowania i histereza magnetyczna ferromagnetyków.
Pierwotna krzywa magnesowania materiału ferromagnetycznego jest to charakterystyka indukcji magnetycznej B w funkcji natężenia pola magnetycznego H . Na podstawie charakterystyki magnesowania można wyznaczyć zależność μ = f(H). Przenikalność magnetyczna ferromagnetyków zmienia się w szerokich granicach. Od niewielkiej wartości początkowej μp wzrasta wraz ze wzrostem natężenia pola magnetycznego, osiąga wartość maksymalną μm, po czym szybko maleje
Jeżeli materiał ferromagnetyczny umieścimy w zewnętrznym polu magnetycznym, to po zaniku pola materiał zachowa pewną polaryzację magnetyczną. Zjawisko to nosi nazwę magnetyzmu szczątkowego, a charakteryzującą go wartość indukcji magnetycznej Br nazywamy pozostałością magnetyczną (rys. 3.11). Pole magnetyczne narastające w kierunku przeciwnym, przy pewnej wartości niweczy magnetyzm szczątkowy. Ta wartość natężenia pola -Hc, potrzebna do otrzymania indukcji magnetycznej równej zeru, nosi nazwę natężenia koercyjnego (koercji). Zmieniając natężenia pola magnetycznego między maksymalnymi wartościami dodatnimi oraz ujemnymi, powoduje się zmianę indukcji magnetycznej, przebiegające według krzywej zamkniętej zwanej pętlą histerezy magnetycznej.
Powierzchnia zawarta wewnątrz pętli histerezy jest proporcjonalna do mocy zużywanej na przemagnesowanie materiału, zwanej stratami na histerezę.
Materiały mające szeroką pętlę histerezy są nazywane magnetycznie twardymi; te zaś, które mają wąską pętlę histerezy - magnetycznie miękkimi.
Podstawowe wielkości i równania obwodów magnetycznych.
Reluktancja lub permeancja odcinka magnetowodu.
Napięcia indukowane w obwodzie zamkniętym i w cewkach. Indukcyjność własna.
Energia pola magnetycznego.
Indukcyjność wzajemna.
Transformator bezstratny.
Warunek okresowości przebiegu czasowego.
Okres, częstotliwość i wartość średnia przebiegu okresowego.
Wielkości przemienne i pulsujące, sinusoidalne i odkształcone.
Wartości skuteczne i wyprostowane (średnie półokresowe).
Współczynnik szczytu.
Współczynnik kształtu.
Przebiegi synchroniczne i kąt przesunięcia fazowego między nimi.
Moc chwilowa i moc czynna oraz współczynnik mocy dwójnika w obwodzie prądu sinusoidalnego.
Elementy R, C, L, M w obwodach prądu sinusoidalnego - połączenia szeregowe i równoległe, reaktancja i suscep-tancja, impedancja i admitancja.
Moce - czynna, bierna i pozorna - dwójnika pasywnego.
Wykresy wskazowe i wykresy trójkąto-we dwójników pasywnych.
Metoda symboliczna - wskazy wirujące, amplitudy i wartości skuteczne zespolone prądu i napięcia.
Zależności między wartościami symbolicznymi prądu i napięcia elementów R L, C.
Impedancja zespolona i admitancja zespolona gałęzi szeregowej R L, C.
Impedancja zespolona i admitancja zespolona układu gałęzi
równoległych R L, C. Zamiana dwójnika R, X na dwójnik G, B, i na odwrót. Moc zespolona dwójnika R X. Moc zespolona dwójnika G, B.
Wyszukiwarka
Podobne podstrony:
Elektryka, Tematy z elektryki
podstawy elektroniki tematy egzaminacyjne
elektryka, Kierunki studiów, Architektura, Materiały do nauki=), Budownictwo, Segregacja tematyczna,
Elektrotechnika IV rok tematy na egzamin styczeń 2010
TEMATY EGZAMINACYJNE TRANSPORT, Nauka, Elektrotechnika
Tematy ćwiczeń i LITERATURA elektronika
Elektra laborki tematy, Materiały polibuda, Semestr IV, elektrotechnika
Tematy egzaminacyjne.do.ELEKTRO, Elektroenergetyka
Wymagania dot. pracy sem, ElektronikaITelekomunikacjaWAT, Semestr 1, Pnor, Tematy na seminarium
Napisy, Tematy kompleksowe, Elektryczność, Sprzęty elektryczne, Urządzenia elektryczne 2
Tematy egzaminacyjne z przedmiotu EiE, Politechnika Łódzka, elektrotechnika
Tematy prac dypl inz-2011-12-2, Elektrotechnika, Downloads
tematypracykontrolnej3semestr, Politechnika Poznańska, Elektrotechnika, Semestr III, I, I, Teoria po
Tematy prac sem. z Pnor, ElektronikaITelekomunikacjaWAT, Semestr 1, Pnor, Tematy na seminarium
Elektrotechnika IV rok tematy na egzamin styczeń 2010
FiltryAdaptacyjne sprawozdanie, Elektrotechnika AGH, Semestr V zimowy 2014-2015 - MODUŁ C, Teoria i
tematy egzaminacyjne z fizyki dla elektroniki
więcej podobnych podstron