Liczby zespolone:

Postać trygonometryczna:

Postać wykładnicza:

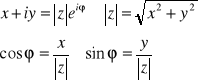
Wzór Moivre'a:

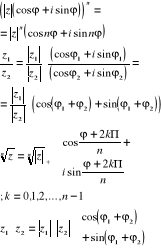
Wzór Taylora:

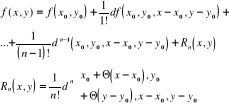
Płaszczyzna styczna:

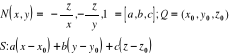
Prosta normalna:

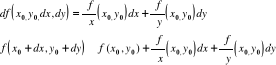
Kryterium porównawcze:

Jeżeli
o wyrazach dodatnich jest zbieżny, to szereg Σz_n jest bezwzględnie zbieżny.

Kryterium d'Alamberta:

Jeżeli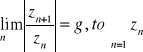
o wyrazach zespolonych jest bezwzględnie zbieżny gdy g<1, natomiast rozbieżny gdy g>1.

Kryterium Cauchy'ego:

Jeżeli
o wyrazach zespolonych jest bezwzględnie zbieżny gdy g<1, natomiast rozbieżny gdy g>1.

Tw. Warunek konieczny i dostateczny:

Warunkiem koniecznym i dostatecznym zbieżności Σz_n o wyrazach z_n=x_n+y_n do sumy S=S₁+S₂i jest jednoczesna zbieżność szeregów Σx_n i Σy_n odpowiedio do sum S₁ i S₂.

Def. Granicy według Heinego:

Def. Granicy według Cauchy`ego:

Def. Logarytm liczby zespolonej:

Liczbę zespoloną w=u+iv nazywamy logarytmem naturalnym z liczby zespolonej z=x+iy≠0 w =ln z, jeżeli e^w=z, ln z=lnz+i(ϕ+2kπ).

Def. Holomorficzność funkcji w punkcie:

Mówimy, że funkcja jest Holomorficzna, jeśli jest różniczkowalna w punkcie z₀ i pewnym jego otoczeniu.

Def. Holomorficzność funkcji w obszarze D: