Przetwarzanie Sygnałów 2 Laboratorium	Ćwiczenie nr. 5 „Dystrybuanta i Gęstość prawdopodobieństwa”
Damian Sosnowski 129003 Wydział Elektroniki Mikrosystemów i Fotoniki Środa 7:30	Data Ćwiczenia: 10. XI. 2004	Ocena:

1. Wyznaczenie gęstości prawdopodobieństwa i dystrybuanty sinusoidy z losową fazą początkową:

Zbadany sygnał to : Sinusoida z losową fazą początkową

y =sin (2πft + φ) gdzie φ to zmienna losowa o rozkładzie jednostajnym na przedziale [-π,π]

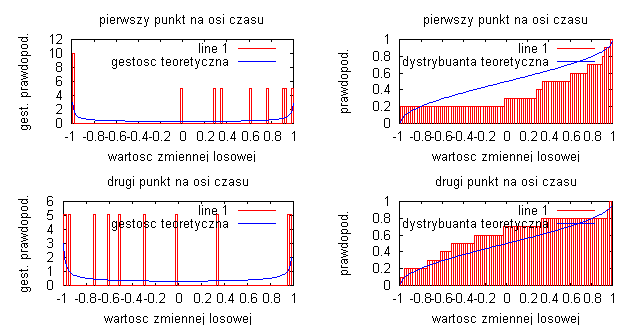
liczba przedziałów obliczania histogramu N=10:

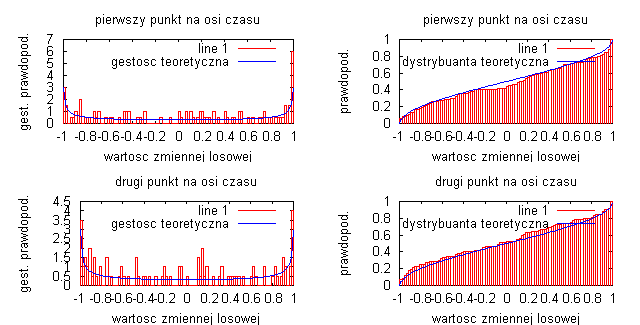
liczba przedziałów obliczania histogramu N=100:

liczba przedziałów obliczania histogramu N=1000:

2. Wyznaczenie gęstości prawdopodobieństwa i dystrybuanty sygnału z losową zmienną o rozkładzie jednostajnym:

Wyznaczyłem gęstość prawdopodobieństwa i dystrybuanty sygnału podstawie wielu obserwacji w zadanych punktach na osi czasu uwzględniając wpływ parametrów estymacji.

Badany sygnał losowy to:

y = α • t gdzie α to zmienna losowa o rozkładzie jednostajnym

na przedziale [0,1]

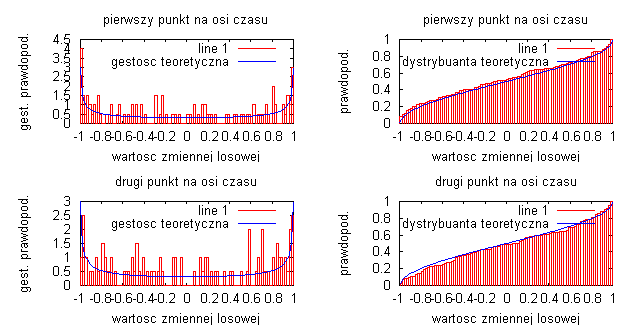
liczba przedziałów obliczania histogramu N=10:

liczba przedziałów obliczania histogramu N=100:

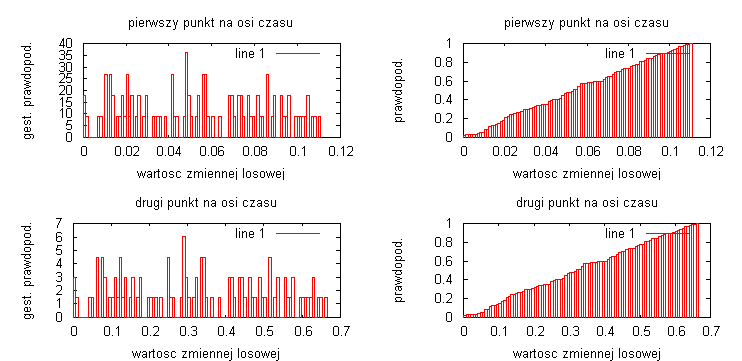
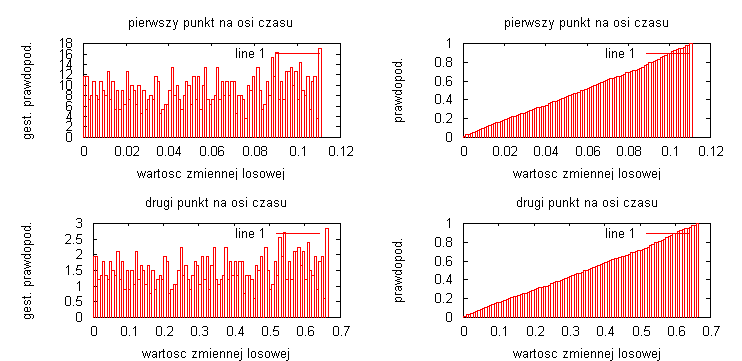
liczba przedziałów obliczania histogramu N=1000:

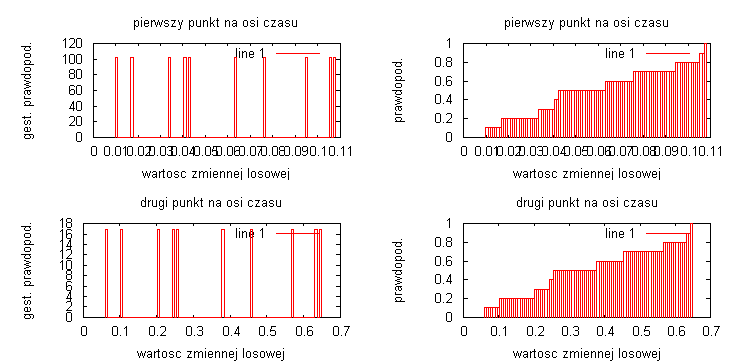
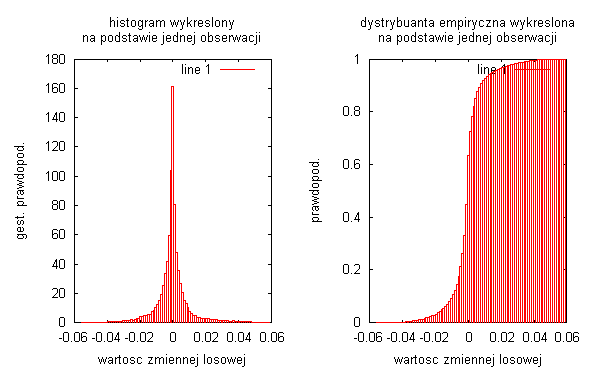
3. Wyznaczenie gęstości prawdopodobieństwa i dystrybuanty dla dwóch wybranych sygnałów mowy:

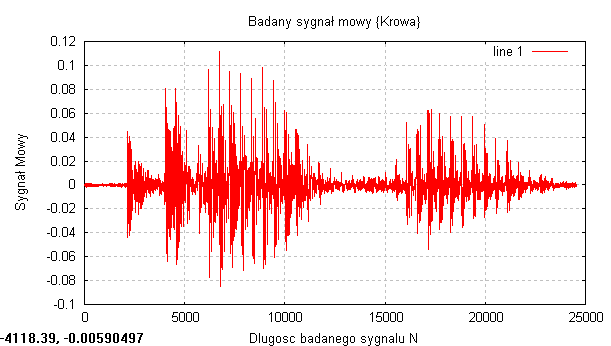
Pierwszym badanym sygnałem był sygnał mowy „Krowa”

Długość sygnału: N=24576

Częstotliwość próbkowania: fs = 48 kHz

Długość sygnału w czasie: 0,512 s.

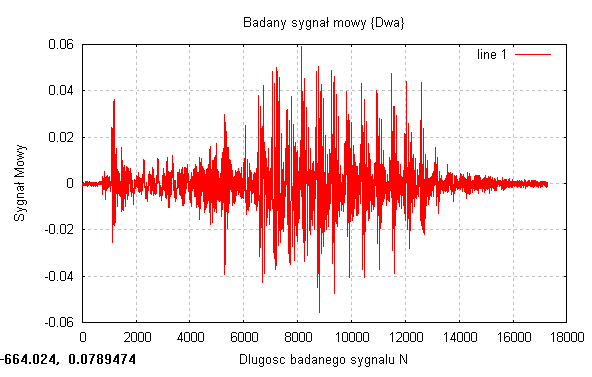
Drugim badanym sygnałem był sygnał mowy „Dwa”

Długość sygnału: N=17280

Częstotliwość próbkowania: fs = 48 kHz

Długość sygnału w czasie: 0,36 s.

4. Wnioski:

Badając sygnał będący sinusoidą z losową fazą początkową widać, że liczba przedziałów obliczania histogramu wpływa na gęstość prawdopodobieństwa i dystrybuanty. Podstawowym wnioskiem jest to, że im dłuższa realizacja procesów (czyli im większa jest liczba obliczania histogramu) tym otrzymane estymatory procesu są lepsze i bardziej dokładnie realizują badany sygnał (obrazuje to linia przerywana na wykresach gęstości prawdopodobieństwa oraz dystrybuanty). Na wykresach jednoznacznie widać podstawowe właściwości dystrybuanty, czyli że jest to funkcja niemalejąca odwzorowująca prawdopodobieństwo, że zmienna losowa w dowolnej chwili czasu jest mniejsza bądź równa wartości x procesu. Wykresy różnią się nieznacznie między sobą, a wynika to z faktu, że za każdym razem generujemy inny przebieg losowy, za pomocą funkcji „random”.

Badając sygnał ze zmienna losową o rozkładzie ponownie widać, że im dłuższa realizacja procesów to otrzymane estymatory są bardziej dokładne i lepiej odwzorowują badany sygnał. Na wykresach nie ma zaznaczonych teoretycznych przebiegów dystrybuanty i gęstości prawdopodobieństwa, ale dla przebiegu y = α • t można jest je przewidzieć: gęstość prawdopodobieństwa jest stała, natomiast dystrybuanta będzie rosła liniowo od 0 do 1. Przebiegi są generowane za pomocą funkcji „random”, toteż znowu widać różnice na wykresach wynikające z losowej generacji przebiegu.

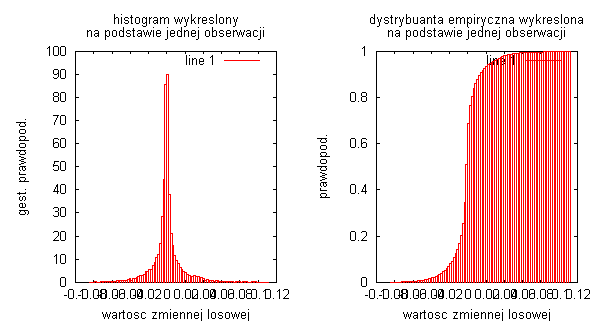
Badając rzeczywiste sygnały, które były sygnałami mowy, widać że największa gęstość prawdopodobieństwa występuje przy punkcie 0, natomiast w miejscach gdzie amplituda sygnału była maksymalna gęstość prawdopodobieństwa była praktycznie równa zero. Otrzymaliśmy troszkę inny rozkład dystrybuanty. W miejscach gdzie badany sygnał był w przybliżeniu stacjonarny czyli na początku i końcu sygnały, gdzie amplituda oscylowała minimalnie wokół zera to dystrybuanta miała niemal stałą wartość (bardzo delikatnie rosła)

1

2