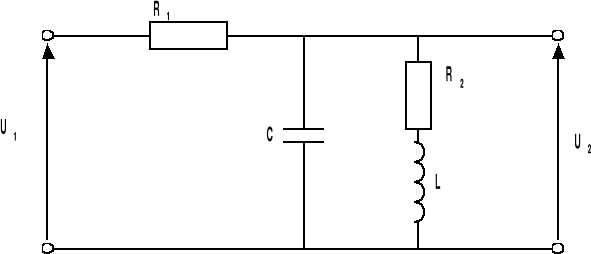
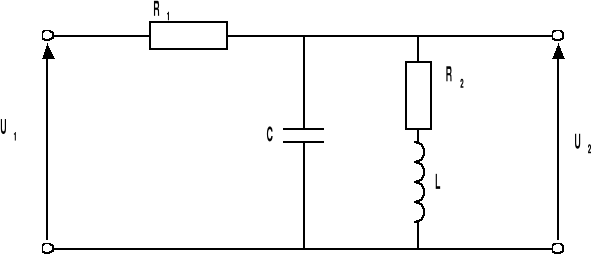
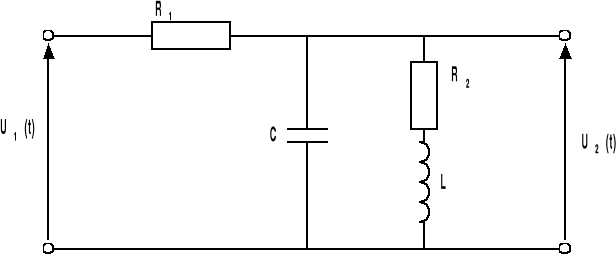
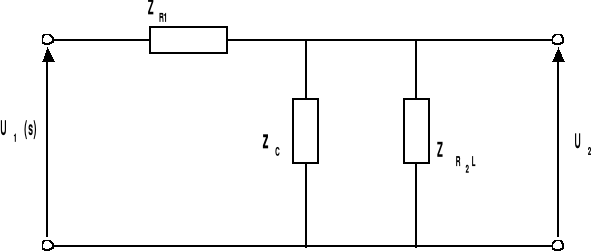
SCHEMAT CZWÓRNIKA:

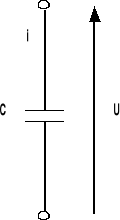
POJEMNOŚĆ KONDENSATORA:
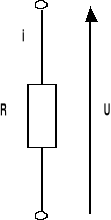
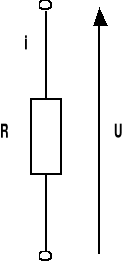
REZYSTANCJA OPORNIKA :
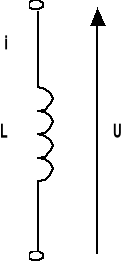
INDUKCYJNOŚĆ CEWKI :
UKŁAD PRZEDSTAWIONY NA POWYŻSZYM RYSUNKU NALEŻY SPROWADZIĆ
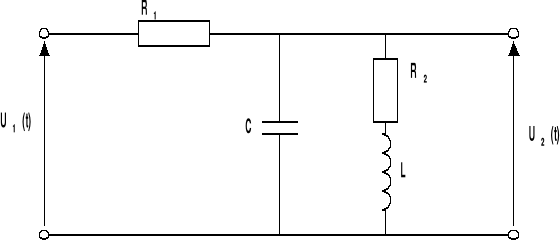
DO POSTACI POZWALAJĄCEJ NA WYZNACZENIE TRANSMITACJI.
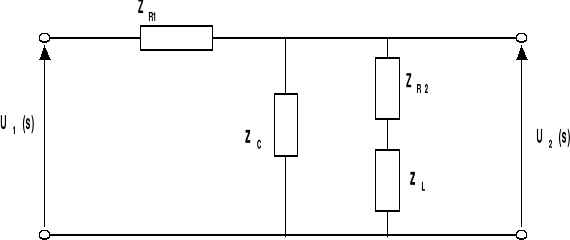
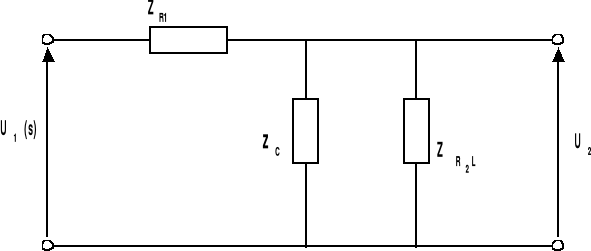
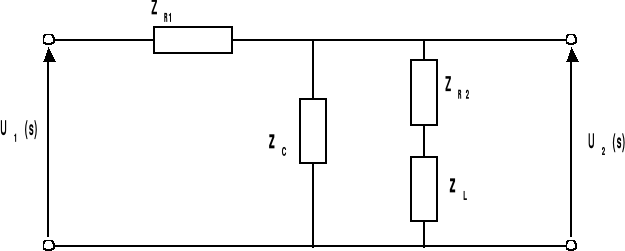
W WYNIKU POŁĄCZENIA RÓWNOLEGŁEGO IMPEDANCJI ZR2 I ZL
OTRZYMUJEMY TAKI OTO UKŁAD ZASTĘPCZY :
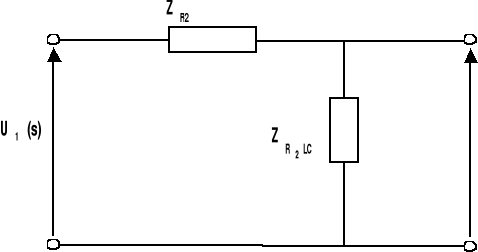
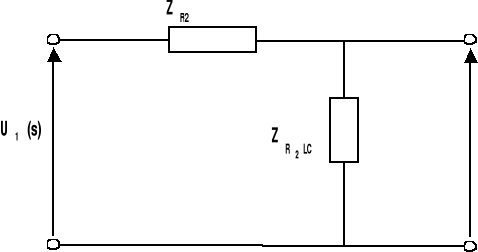
POPRZEZ POŁĄCZENIE SZEREGOWE IMPEDANCJI ZC I ZR2L OTRZYMUJEMY NASTĘPUJĄCY UKŁAD ELEKTRYCZNY :
U1(s) = J(s) (ZR1 + ZR2LC)
U2(s) = J(s) ![]()
ZR2LC
ZR = R1
ZR2 = R2
ZC = ![]()
ZL = s L
ZR2LC = R2 + s L
P0ŁĄCZENIE SZEREGOWE : ZR2L = ZR2+ ZR2LC
P0ŁĄCZENIE RÓWNOLEGŁE :![]()
= ![]()
= ![]()
ZR2LC = ![]()
ZR2LC = 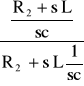
= ![]()
G(s) =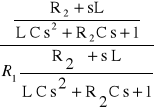
G(s) = 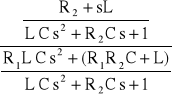
T1 = ![]()
, T2 = ![]()
, T3 = ![]()
k = ![]()
PODSTAWIAJĄC T1 T2 T3 OTRZYMUJEMY G(s) RÓWNE :
G(s) = ![]()
PRZYJMUJĘ :
L = 100 [mH]
C = 1000[μF]
R1 = 80[Ω]
R2 = 1[Ω]
T1 = 0,1
T2 = 9,877*10-5
T3 = 9,877*10-4
k = 0,012
x(t) - WYMUSZENIE.
y(t) - ODPOWIEDŹ UKŁADU NA WYMUSZENIE.
G(s) = ![]()
CHARAKTERYSTYKA SKOKOWA :
X(t) = K * 1(t)
L[X(t)] = X(s) = ![]()
*K
PRZYJMUJĘ K = 12
G(s) = ![]()
Y(s) = G(s) X(s)
Y(t) = L-1[G(s) X(s)]
h(t) = Y(t) ( PONIEWAŻ WYSTĘPUJE WYMUSZENIE SKOKOWE )
h(t) = K k [exp (![]()
t) [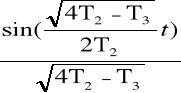
(2 T1−T3) − cos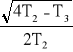
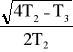
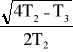
(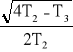
t) ] + 1]
h(t) = exp (−5 t) [1,238 sin (100,499 t)−0,123 cos (100,499 t) ] +0,123
t |
0 |
0,001 |
0,1 |
0,1 |
1 |
10 |
100 |
∝ |
h(t) |
0 |
0,125 |
1,054 |
−0,225 |
0,122 |
0,123 |
0,123 |
k K=0,123 |
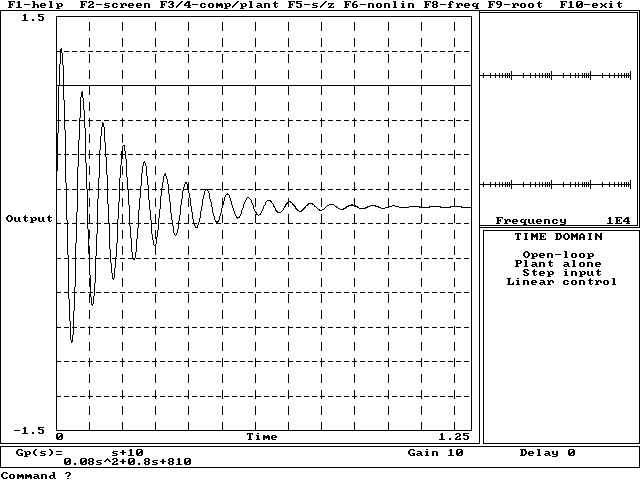
CHARAKTERYSTYKA SKOKOWA :
CHARAKTERYSTYKI CZĘSTOTLIWOŚCIOWE :
G(iω) = ![]()
+i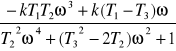
P(ω) = ![]()
Q(ω) = 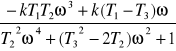
ω |
0 |
0,01 |
0,1 |
1 |
10 |
100 |
1000 |
|
P(ω) |
0,012 |
0,012 |
0,012 |
0,012 |
0,013 |
1,246 |
1,202*10 |
0 |
Q(ω) |
0 |
1,22*10 |
1,22*10 |
1,22*10 |
0,012 |
0,031 |
-0,013 |
0 |
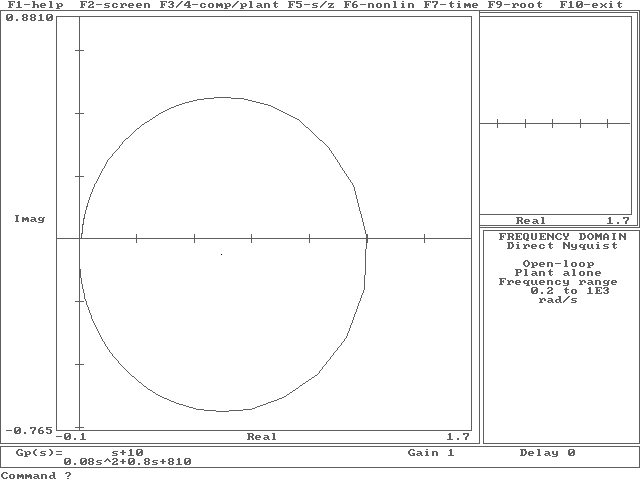
A(ω) = ![]()
=G(iω)
G(iω) = ![]()
A(ω) = k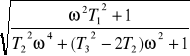
ϕ(ω) = arg [G(iω)] = arc tg (![]()
)
ω |
0 |
0,01 |
1 |
10 |
100 |
1000 |
|
A(ω) |
0,012 |
0,012 |
0,012 |
0,018 |
1,247 |
0,013 |
0 |
ϕ(ω) = arc tg 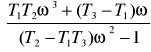
ω |
0 |
0,01 |
1 |
10 |
70 |
100 |
105 |
1000 |
|
ϕ(ω) |
0 |
0,057 |
5,6 |
44,4 |
74,2 |
1,4 |
-45 |
-89,90 |
-90 |
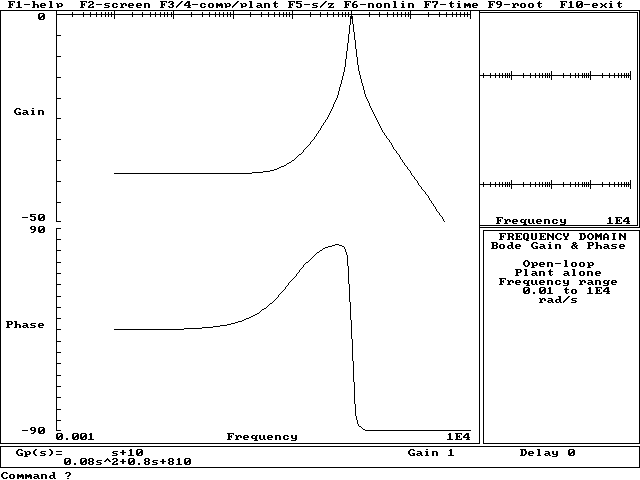
WNIOSKI
:
POPRZEZ OKREŚLENIE POWYŻSZYCH ZALEŻNOŚCI AUTOMATYCZNYCH
POLEGAJĄCYCH NA WYZNACZENIU TRANSMITANCJI , ORAZ PRZEZ ZOBRAZOWNIE TYCH ZALEŻNOŚCI NA WYKRESACH MOŻNA WYWNIOSKOWAĆ ŻE DANY CZWÓRNIK ELEKTRYCZNY JEST FILTREM
PASMOWOPRZEPUSTOWYM.
i(t) = ![]()
u(t) = ![]()
i(t) = C![]()
L I(s) = C s U(s)
![]()
= Zc(s) = ![]()
U(t) = R i(t) ZR(S) = R
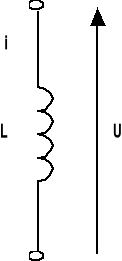
U(t) = L ![]()
L U(s) = L s I(s)
ZL(s) = s L
L
G(s) = ![]()
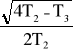
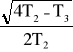
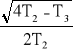
U2(s)