Janusz Kucaba 19.11.2005r.

I TD

Sprawozdanie z ćw. nr4

Pomiar współczynnika lepkości cieczy

1. Zagadnienia do samodzielnego opracowania.

1. Ciecz doskonała, ciecz rzeczywista, lepkość cieczy.

Cieczą doskonałą nazywamy ciecz nieściśliwą i nielepką. Ciecz nieściśliwa to ciecz, która nie zmienia swojej objętości pod wpływem zmian ciśnienia. W cieczy doskonałej nie jest zużywana energia na zmianę objętości i jeżeli pominiemy zmiany temperatury cieczy, to możemy stosować do niej zasadę zachowania energii mechanicznej. Z zasady tej można wyprowadzić równanie Bernoulliego:

Gdzie: p0- ciśnienie w strudze poruszającej się cieczy,

h- wysokość wzniesienia w danym miejscu strugi,

v- prędkość cieczy w danym miejscu,

ρ- gęstość cieczy.

Z równania tego wynika, że w poruszającej się cieczy ciśnienie nie musi mieć stałej wartości.

Gdy w strudze cieczy rośnie prędkość przepływu v, wówczas maleje ciśnienie p.

Ciecze rzeczywiste są cieczami lepkimi. Wskutek tarcia, występującego między cząsteczkami cieczy, poruszająca się cząsteczka pociąga za sobą cząsteczki z nią sąsiadujące.

Każdą ciecz można scharakteryzować odpowiednim dla niej współczynnikiem lepkości.

Współczynnik proporcjonalności η nazywa się dynamicznym współczynnikiem lepkości cieczy.W układzie Si ma wymiar:

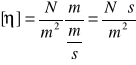
Lepkością lub tarciem wewnętrznym nazywamy zjawisko występowania sił stycznych przeciwstawiających się przemieszczeniu jednych części ciała względem innych jego części . Wskutek tarcia występującego między cząsteczkami cieczy lub gazu , poruszająca się cząsteczka pociąga za sobą cząsteczki sąsiadujące z nią z prędkością tym bardziej zbliżoną do prędkości własnej , im ciecz lub gaz są bardziej lepkie . Analogicznie cząsteczka spoczywająca hamuje poruszające się cząsteczki sąsiednie . Ciecz przepływającą przez rurę możemy podzielić ją na warstwy równoległe do osi rury , koncentryczne w przypadku rury okrągłej . Warstwa cieczy przylegająca do ścianek rury znajduje się w spoczynku , w kierunku osi rury prędkość warstw cieczy wzrasta , osiągając prędkość maksymalną na osi rury . Przy małych prędkościach przepływ cieczy rzeczywistej przez rurę gładką jest przepływem laminarnym ( warstwowym ) .Przepływ cieczy nazywamy przepływem laminarnym , jeżeli prędkość w każdym punkcie przekroju jest jednoznacznie określona . Gdy prędkość maksymalna przepływu cieczy wzrasta , laminarny stan ruchu zanika . Prędkość przestaje być funkcją ciągłą współrzędnych położenia. Taki stan ruchu cieczy nazywamy stanem turbulentnym . Istnieje pewna prędkość krytyczna , powyżej której ruch cieczy przestaje być ruchem laminarnym.

2. Ruch kulki w cieczy lepkiej (prawo Stokesa).

Dla małych prędkości, siła tarcia wewnętrznego R jest wprost proporcjonalna do prędkości v, zależy również od wymiaru liniowego l ciała oraz od współczynnika lepkości i wynosi:

R = -6π r η v

Na kulkę o promieniu r, spadającą w lepkiej cieczy, działają siły:

F_g= mg = ρ v g

F_w= - ρ_c V g

R = -6π r η v, gdzie ρ - gęstość ciała stałego

ρ_c - gęstość cieczy

V = 4/3 π r³

Wypadkowa siła F wynosi:

F = F_g - F_w - R

Siła F jest z czasem malejąca, przyspieszenie ciała maleje więc, a prędkość dąży do wartości, gdy F= 0. Różniczkując powyższe równanie, można otrzymać wartość prędkości kulki:

v = A/B(1 - e^-Bt)

Prędkość graniczna, jest prędkością stałą i wynosiv_g = A/B. W rzeczywistości kulka po niedługim czasie porusza się z prędkością bardzo bliską v_{g ,} więc prędkość graniczna jest dobrym przybliżeniem rzeczywistej prędkości kulki.

2. Wykonanie ćwiczenia.

Układ pomiarowy składa się z rury szklanej wypełnionej gliceryną, do której

wrzucane są kulki (ołowiane lub stalowe).

1. Zmierzyć średnicę kulki (śrubą mikrometryczną). Pomiar wykonać kilka razy i

ocenić błąd  r .

2. Zaznaczyć na rurze szklanej drogę kulek s (odcinek liczący od 0,5 do 1m). Górny

koniec odcinka powinien znajdować się około 20 do 25cm poniżej poziomu cieczy,

gdyż w pierwszej fazie ruch kulki nie odbywa się ze stałą prędkością.

3. Wrzucić kulkę do cieczy (tuż nad powierzchnią). Zadbać o to, żeby kulka wpadła do cieczy w środku przekroju cylindra, tak, aby ruch kulki odbywał się w możliwie jak

największej odległości od ścian cylindra.

4. Zmierzyć sekundomierzem czas t, w którym kulka przebywa zaznaczoną drogę.

5. Pomiary wykonać, dla co najmniej 4 kulek, powtórzyć każdy pomiar trzy razy.

Gęstość kulek:

- żelazo: ρk=7875

Gęstość gliceryny: ρc=1230

3. Wyniki pomiarów

Lp.	2r	r	s	t	η	ηr śr.	ηr śr.±Δη
		[mm]	[mm]	[cm]	[s]	[ ]	[ ]	[ ]
1	3,17	1,585	90	5,35	0,22	0,22	0,22±0,01
2	3,17	1,585	90	5,44	0,22	0,22	0,22±0,01
3	3,17	1,585	90	5,39	0,22	0,22	0,22±0,01
4	3,17	1,585	90	5,22	0,21	0,22	0,22±0,01
5	3,17	1,585	90	5,31	0,21	0,22	0,22±0,01
6	3,17	1,585	90	5,31	0,21	0,22	0,22±0,01
7	3,17	1,585	90	5,43	0,22	0,22	0,22±0,01
8	3,17	1,585	90	5,33	0,22	0,22	0,22±0,01

4. Obliczenia.

Δr = 0,01 mm = 0,00001 m

Δt = 0,2 s

Δs = 0,6 cm = 0,006 m

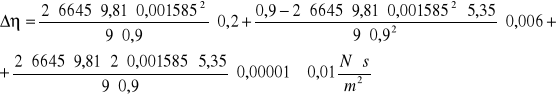
V. Wnioski.

Celem ćwiczenia był pomiar współczynnika lepkości cieczy metodą Stokesa.

Dokonaliśmy pomiaru średnicy kulek przy użyciu śruby mikrometrycznej. Pomiary średnicy powtórzyliśmy czterokrotnie w celu uzyskania większej dokładności pomiarów.

Wpływ ścianek bocznych oraz wysokości słupa cieczy na współczynnik lepkości jest spowodowany zasadą powstawania zjawiska lepkości (przekazywanie sobie pędu przez sąsiadujące ze sobą warstwy cieczy). Im bliżej ścianki znajduje się poruszająca się powierzchnia kulki (warstwa cieczy przy powierzchni kulki), tym bardziej jest hamowana przez nieruchomą ściankę naczynia (warstwę cieczy przy powierzchni ścianki naczynia).

---