Zawartość

CIĄGI

1. WIADOMOŚCI OGÓLNE:

Ciąg liczbowy to funkcja f: N→R.

Dla ustalonej liczby nϵN, wartość f(n) nazywamy n-tym wyrazem ciągu i oznaczamy a_n .

(a_n)_n ∈ N a_n- zbiór wyrazów ciągu.

(a_n)n=1

1. Wzór na n-ty wyraz ciagu

a_n=

2. Wzór rekurencyjny

a₁=1

a₂=2

a_n=a_n-2 + a_n-1 , n≥3

3. Wzór opisowy

a_n- n-ta liczba w rozwinięciu dziesiętnym liczby

2. MONOTONICZNOŚĆ:

a_n+1 > a_n rosnący

a_n+1 < a_n malejący

a_n+1= a_n stały

Przykład:

Sprawdź czy ciąg jest malejący.

3. GRANICE CIĄGÓW

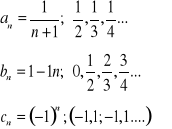
Dla c_n granica nie istnieje.

Gdy n rośnie, to wyrazy ciągu a_n zbliżają się coraz bardziej do a=0, podobnie dla ciągu b_n , b=1, a dla ciągu c_n nie istnieje liczba c, do której zbliżają się wyrazy ciągu c_n.

Def:

Mówimy, że ciąg d_n ma skończoną granicę d, co zapisujemy:

LICZBA e

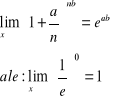
Notatki z wykładu (M. Wilczyński)

1