ANALIZA WSPÓŁZALEŻNOŚCI DWÓCH CECH

Tablica dwudzielcza cech X i Y

X \ Y	. . .
	. . . . . .
	. . .	n

- liczba elementów próby, które odpowiadają poziomowi
cechy X i poziomowi
cechy Y.

(n - co najmniej kilkadziesiąt ,
)

Statystyka chi-kwadrat:

,

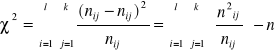
gdzie
są tzw. liczebnościami teoretycznymi.

Wskaźnik kontyngencji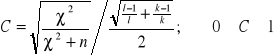
.

Większe wartości C wskazują na silniejszą współzależność
cech X i Y.

Tablica dwudzielcza cech mierzalnych X i Y nosi nazwę tablicy korelacyjnej.

Jeżeli zmienne X i Y są ciągłe, to wartości
i
są środkami przedziałów klasowych.

W tablicy korelacyjnej zawarte są rozkłady brzegowe zmiennej X (pierwsza i ostatnia kolumna) oraz zmiennej Y (pierwszy i ostatni wiersz).

Wybrane charakterystyki liczbowe rozkładów:

• Średnie brzegowe:
  

• Wariancje ogólne:
  

Współczynnik korelacji cech mierzalnych

Służy do oceny kierunku i siły zależności liniowej między zmiennymi X i Y:

;

gdzie:
,

zaś
są odchyleniami standardowymi odpowiednio cechy X oraz Y.

.

Bliższe zera wartości
wskazują na słabszą zależność liniową między cechami X i Y.

Współczynnik determinacji
informuje jaka część całkowitej zmienności cechy przyjętej za wynikową (objaśnianą) jest wyjaśniana przez zmiany cechy przyjętej za wejściową (objaśniającą).

3