Przenoszony moment skręcający Ms,
Średnice toczne:d1 i d2 .
Nominalny kąt zarysu zębów
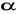
.Kąty nachylenia zębów: b1 i b2 .
Odległości wg rysunku.
β
Obliczenia wałka pośredniego 2- st. przekładni walcowej
Dane:
Przenoszony moment skręcający Ms,
Średnice toczne:d1 i d2 .
Nominalny kąt zarysu zębów ![]()
.
Kąty nachylenia zębów: b1 i b2 .
Odległości wg rysunku.
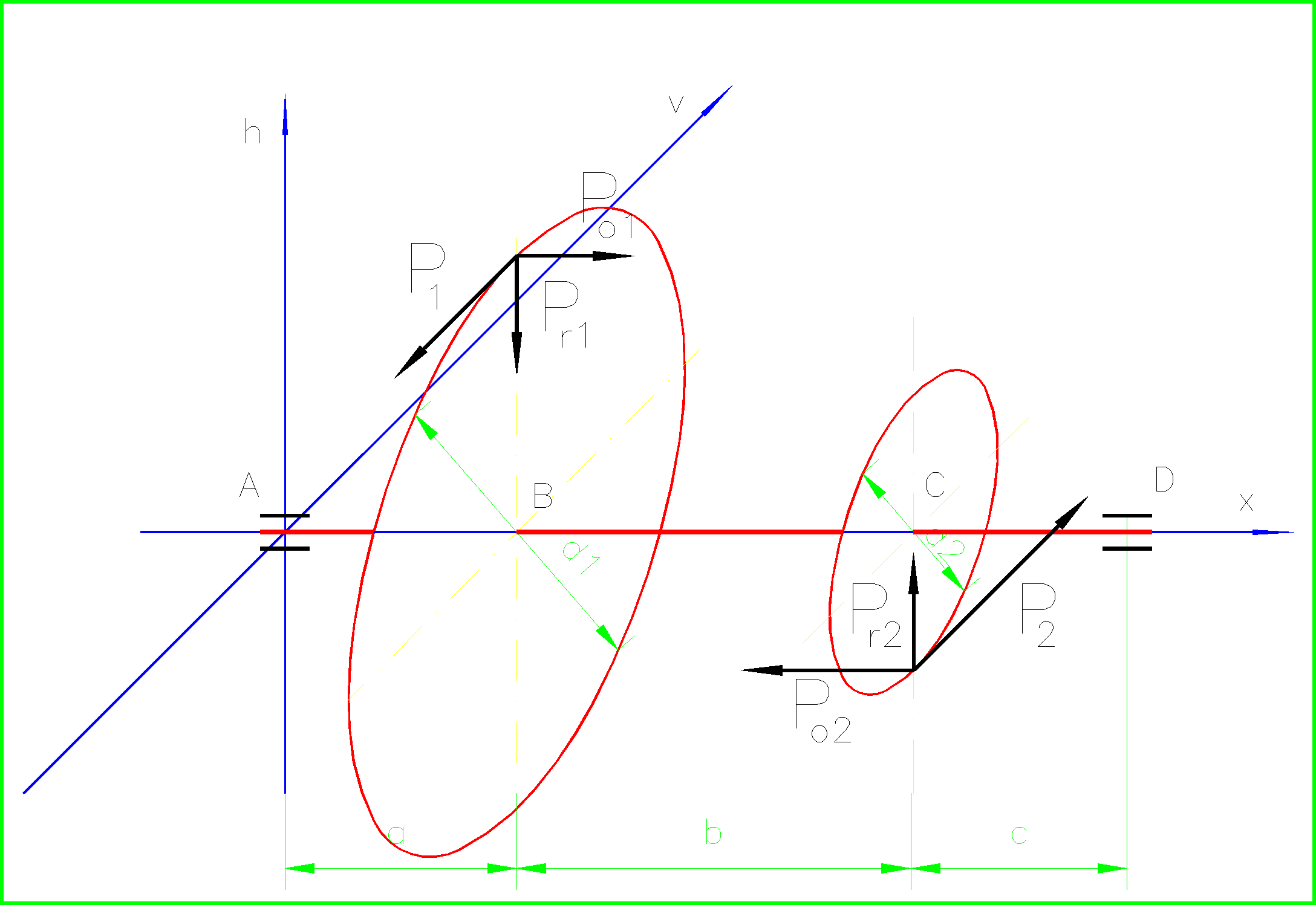
Siły międzyzębne
Siły obwodowe
![]()
,
Siły promieniowe
![]()
Siły osiowe
![]()
![]()
,
Obliczenia wałka
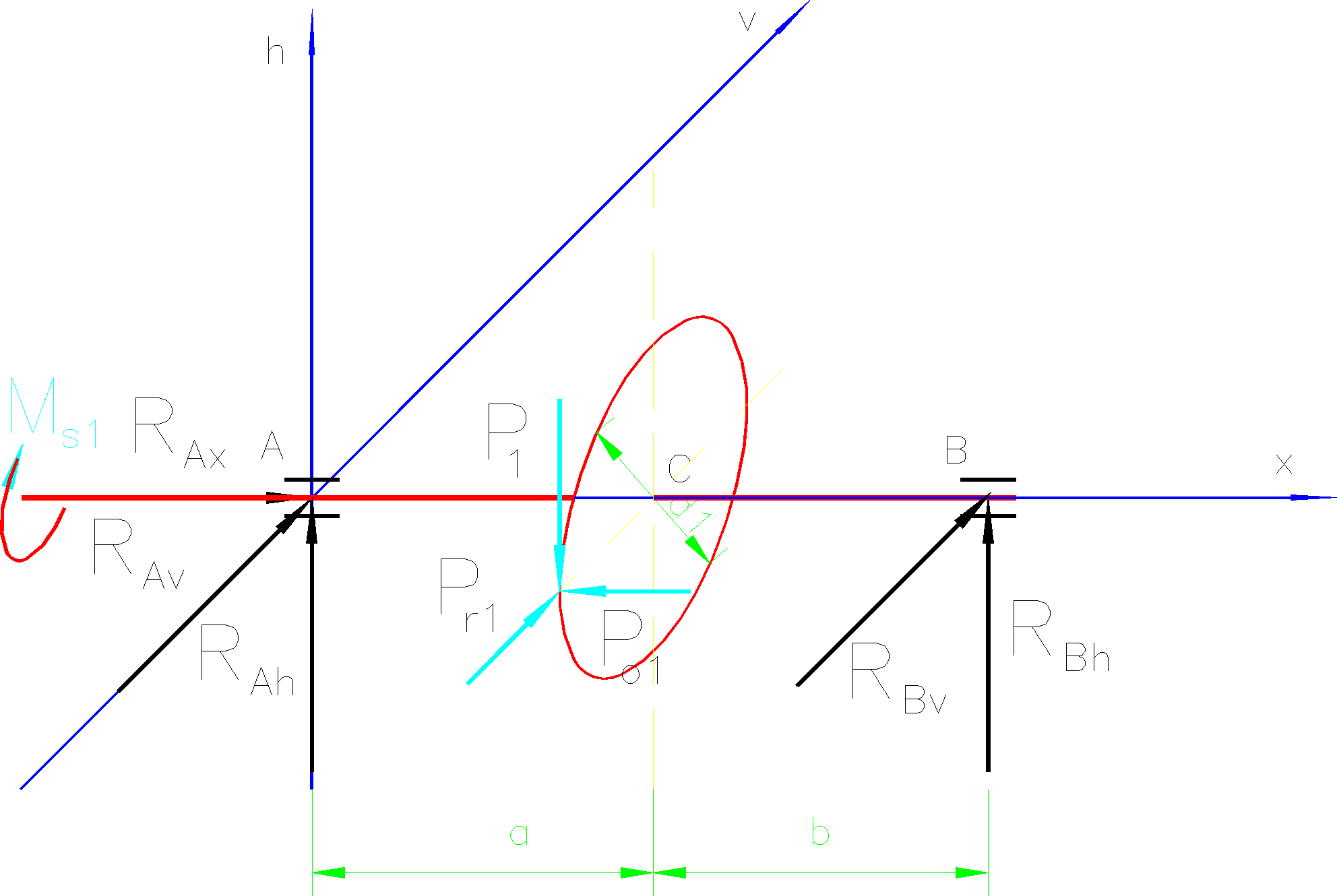
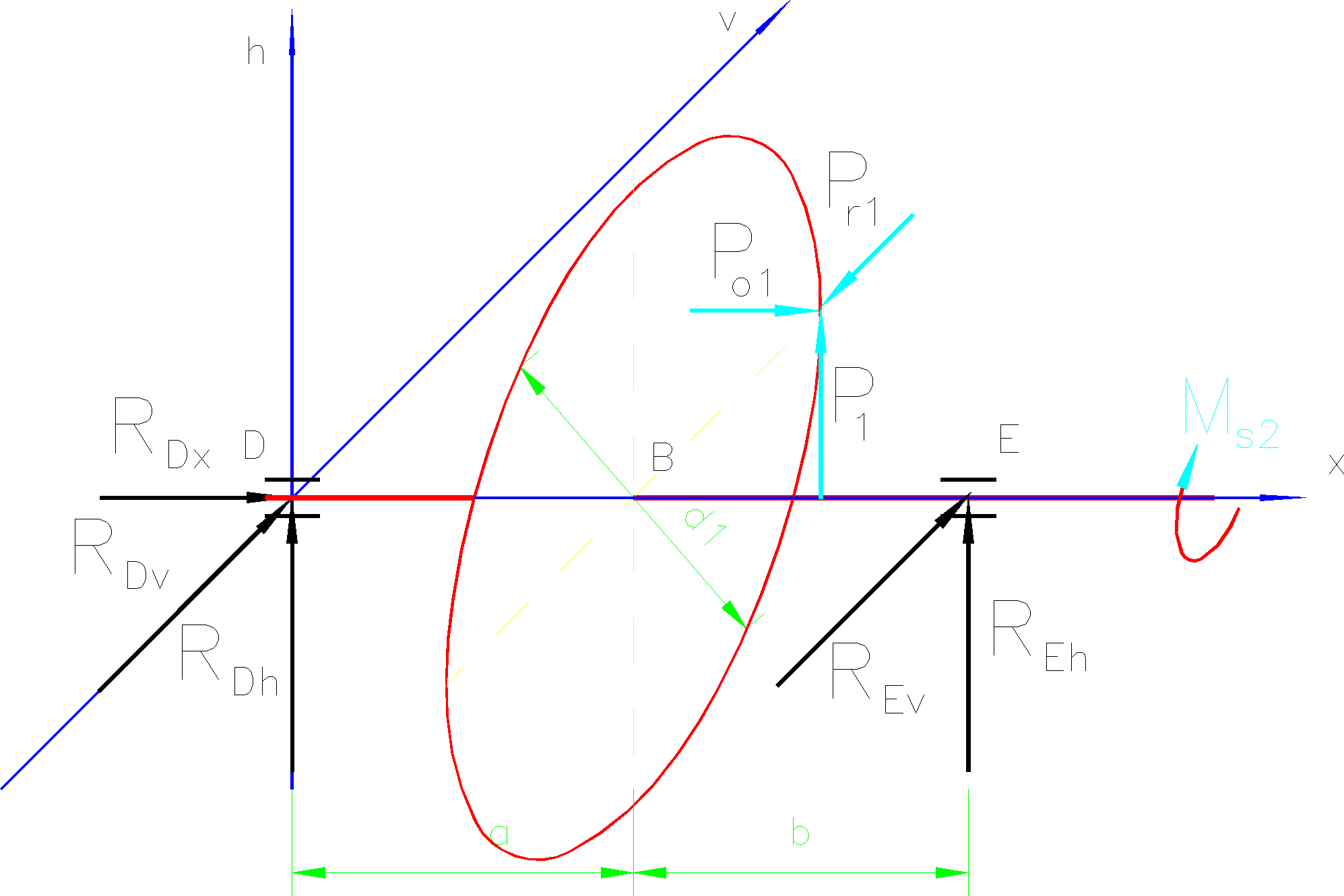
Układ sił obciążających wałek przedstawiono na rys.1.
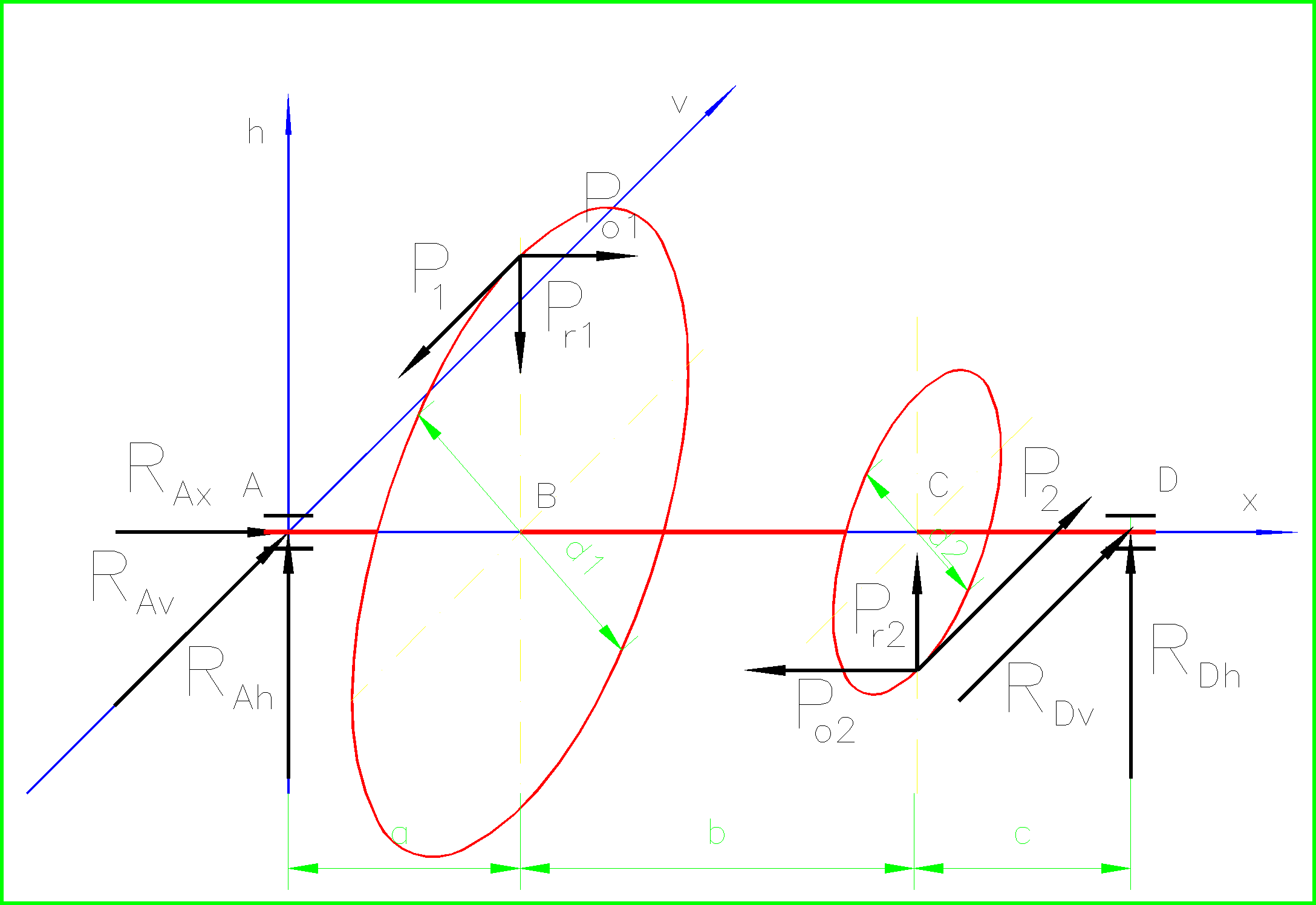
W płaszczyźnie h-x:
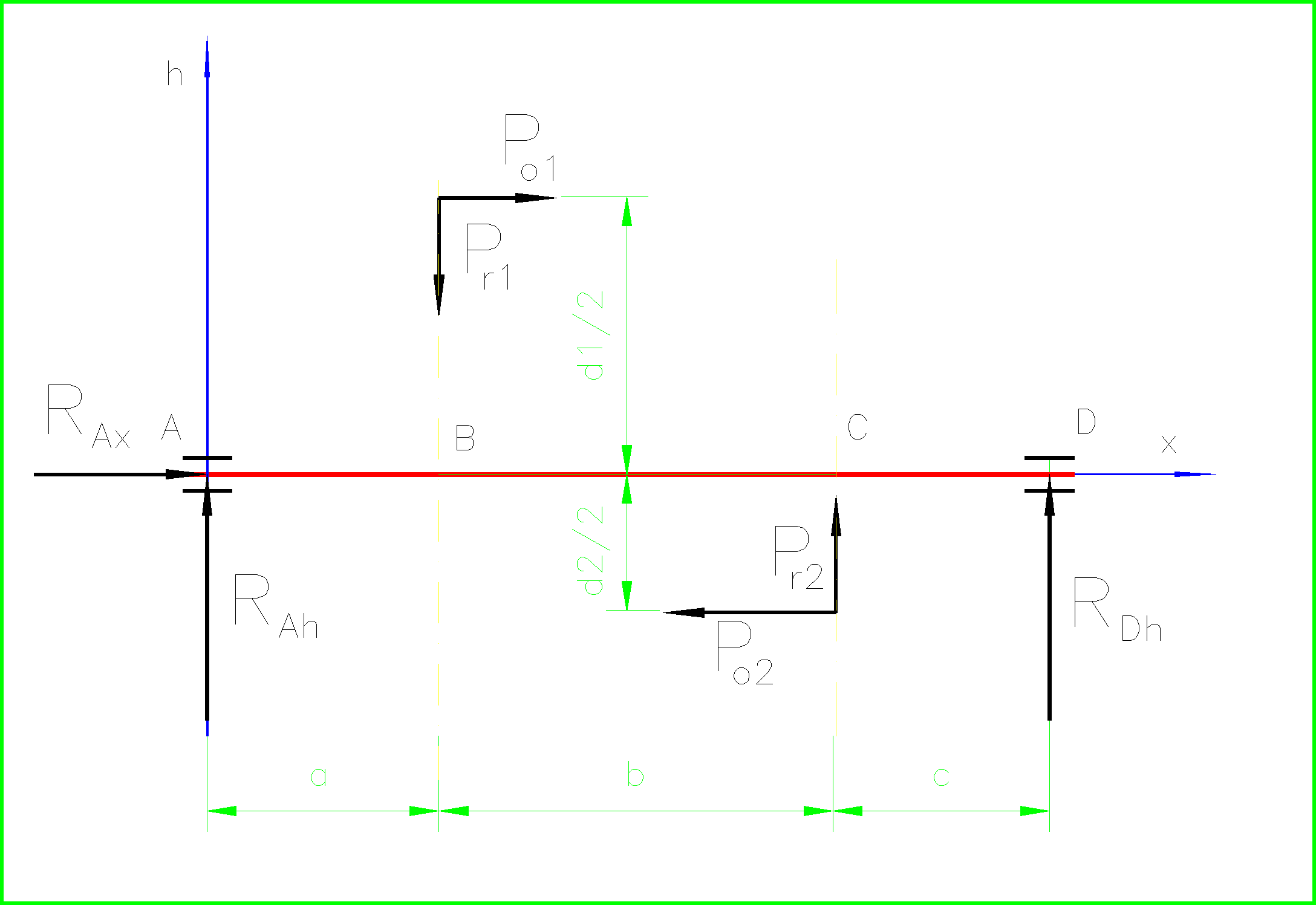
3.1 Obliczenia reakcji składowych na podporach RDh i RAh
Suma momentów względem punktu A
Σ MiA= RBh*(a+b+c)+Pr2*(a+b)-Po2*d2/2-Po1*d1/2-Pr1*a= 0 ,
Suma momentów względem punktu D
Σ MiD= RAh*(a+b+c)+Pr2*c+Po2*d2/2+Po1*d1/2-Pr1*(b+c)= 0,
stąd obliczamy składowe „h” reakcji RDh i RAh w punktach D i A
suma sił wzdłuż osi Ax
Σ PiA= RAx +Po1 -Po2 =0
pozwala policzyć składową „x” reakcji RA .
3.2 Obliczenie momentów gnących w płaszczyźnie h-x, w punktach A, B, C i D.
W punktach B, C z obu stron (siły poosiowe powodują skok momentu gnącego).
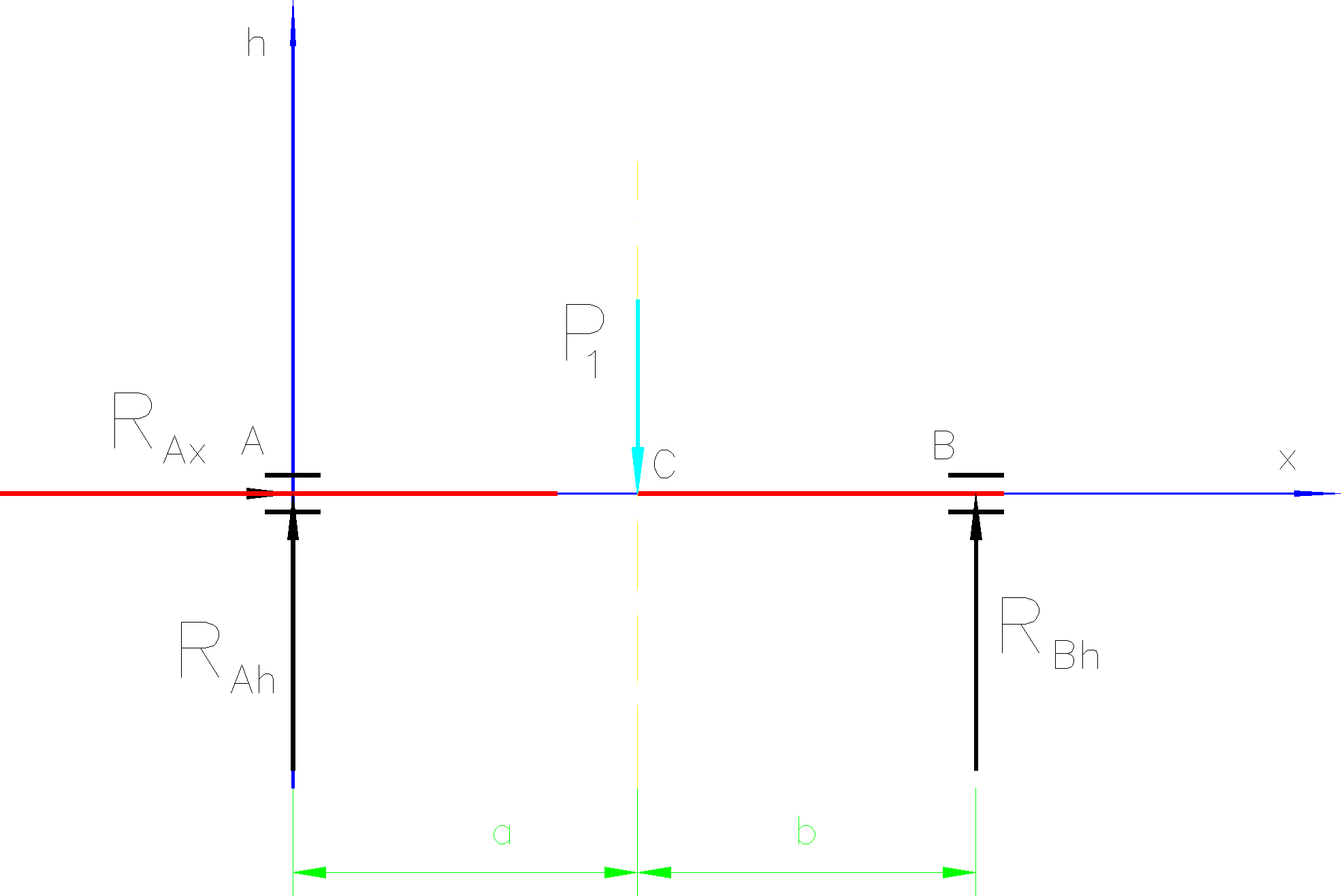
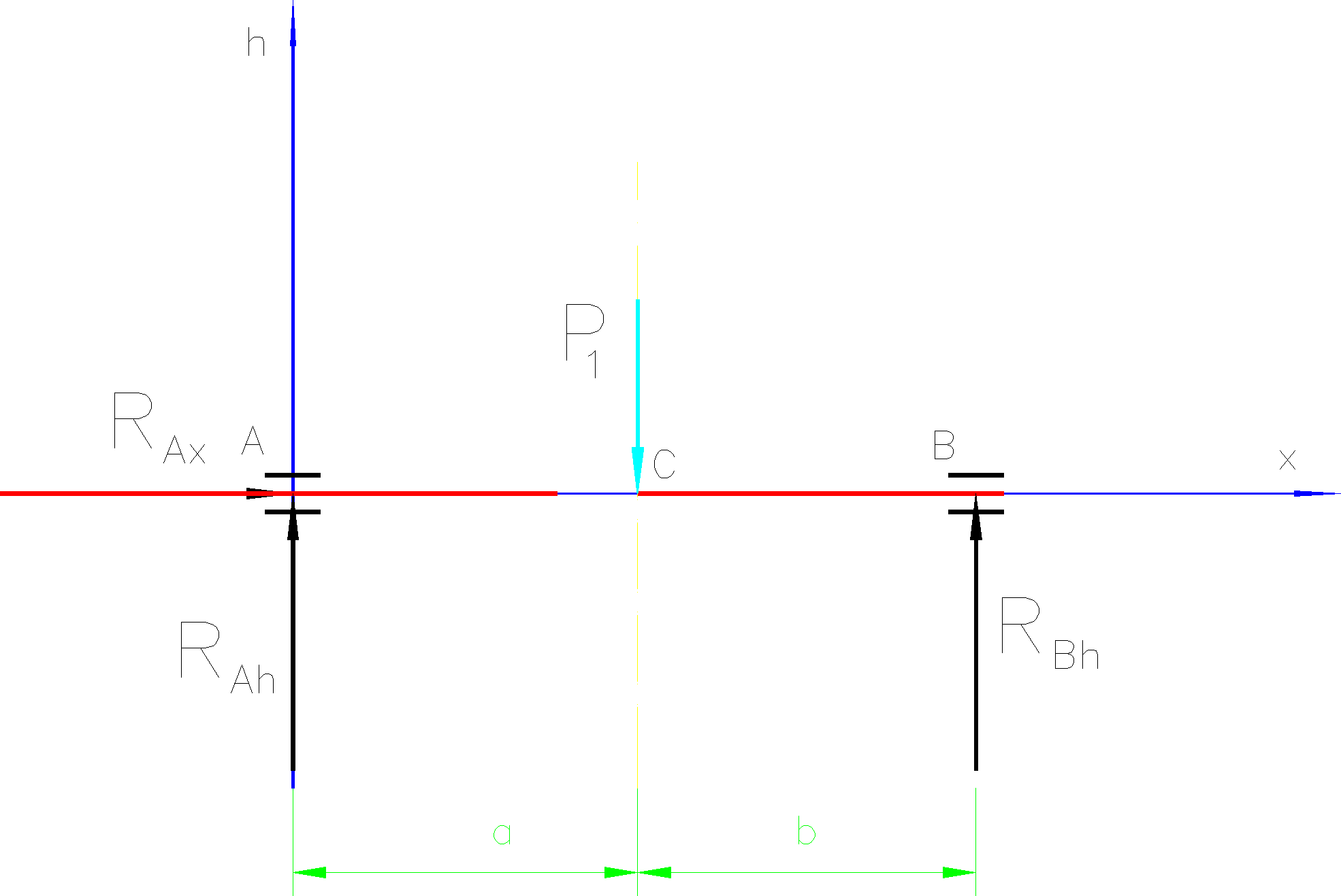
W płaszczyźnie v-x:
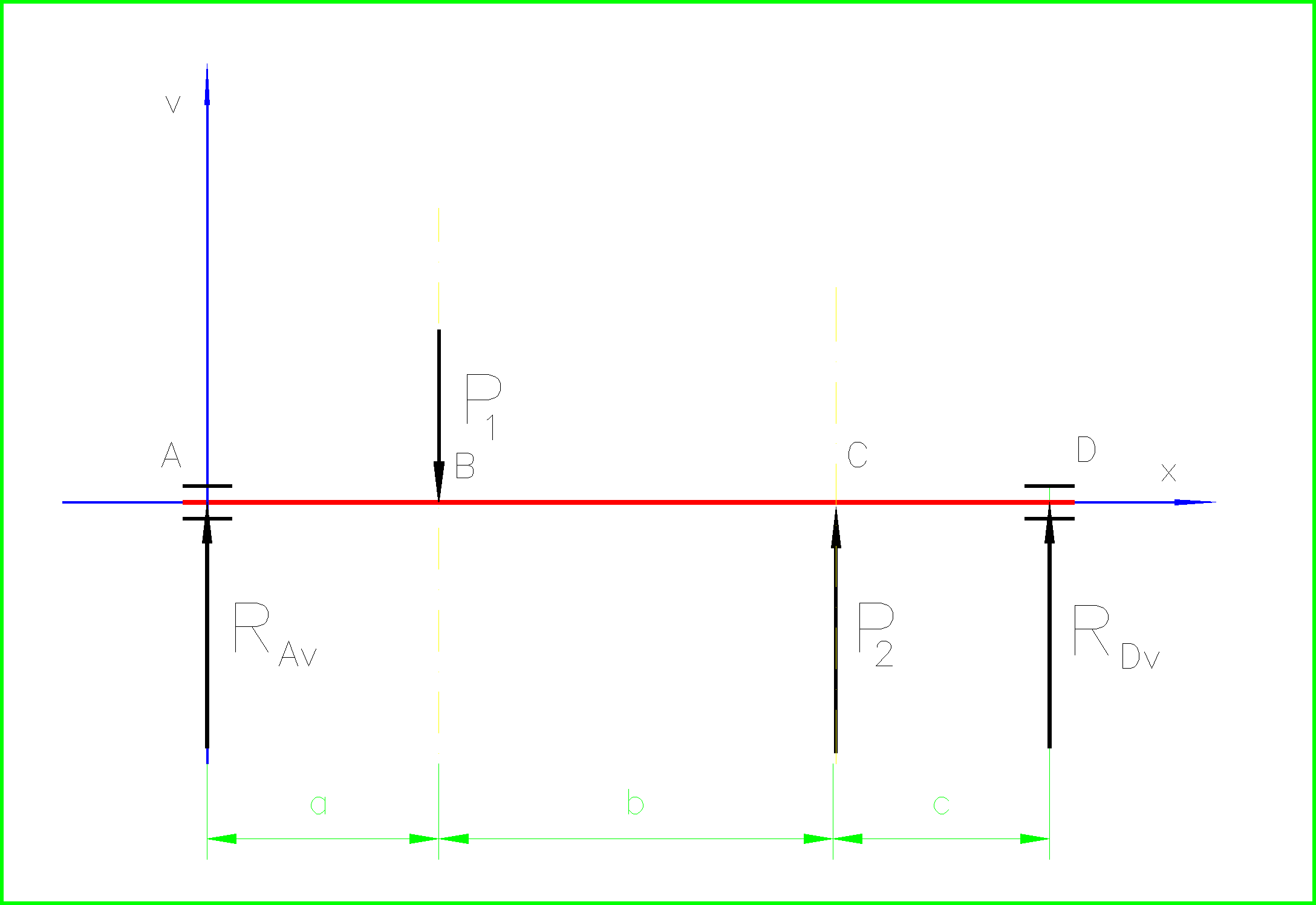
3.3 Obliczenia reakcji składowych na podporach RAv i RDv
Suma momentów względem punktu A
Σ MiA= RDv*(a+b+c)+P2*(a+b)-P1*a = 0 ,
Suma momentów względem punktu D
Σ MiD= RAv*(a+b+c)+P2*c-P1*(b+c) = 0,
stąd obliczamy składowe „v” reakcji RDv i RAv w punktach D i A
3.4 Obliczenie momentów gnących w płaszczyźnie v-x w punktach A, B, C i D.
3.5 Całkowite reakcje promieniowe (wypadkowe) na podporach
![]()
,
![]()
3.6 Całkowite momenty gnące (wypadkowe) w punktach A, B, C, D.
![]()
dla k={A, B, C, D },
przy czym
MgA= 0
![]()
![]()
, ![]()
,
![]()
![]()
, ![]()
,
![]()
, MgD= 0.
3.7 Obliczenie momentów zastępczych w punktach A, B, C, D.
![]()
,
gdzie: 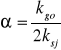
.
Na granicach przedziałów momenty zredukowane wynoszą
MzA=0
![]()
, ![]()
![]()
, ![]()
MzD=0
3.8 Średnicę wałka w dowolnym punkcie liczymy stosując wzór
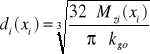
Części wałka o długościach „a” i „c” zaleca się podzielić na kilka przedziałów
i w otrzymanych punktach podziału obliczyć teoretyczną średnicę (lub promień wałka).
Zarys wałka rzeczywistego powinien być ukształtowany na zewnątrz wałka teoretycznego, uwzględniając znormalizowane wartości średnic czopów
pod łożyska toczne, uszczelnienia i wpusty.
5