Skład zespołu		Batyra Artur	Dębiec Wojciech	Krzysztof Gębarowski
Wydział	WNiG	Grupa 1	Rok 2	Data 14.04.07

1. Cel ćwiczenia.

Celem ćwiczenia jest określenie stosunku prędkości średniej do maksymalnej, przy przepływie płynu przez przewód, w zależności od liczby Raynoldsa. W ćwiczeniu bada się przepływ powietrza przez przewód o przekroju kołowym.

2. Wzory z których korzystaliśmy:

Poszukiwana funkcja v(r) może być zapisana w postaci:

gdzie
- dynamiczny współczynnik lepkości

Funkcja w osi przewodu ma maksimum równe:

Całkując prędkość po powierzchni przekroju przewodu, oblicza się strumień objętości

Prędkość średnią można wyznaczyć z definicyjnej zależności:

Z tego widać, że w ruchu laminarnym prędkość średnia równa jest połowie prędkości maksymalnej.

W przepływie turbulentnym profil prędkości różni się znacznie od rozkładu prędkości odpowiadającego ruchowi laminarnemu. Prędkość nieznacznie zmienia się w podstawowym rdzeniu strumienia płynu i szybko maleje w pobliżu ścianek. Bezpośrednio przy ściance przewodu znajduje się laminarna warstwa przyścienna o grubości ρ, w której prędkość jest liniową funkcją zmiennej r.

gdzie
- naprężenia styczne na ściance.

Natomiast w pozostałej części przekroju profil prędkości w ruchu turbulentnym wyraża funkcja:

Z zależności przy założeniu, że ρ << R określa się średnią prędkość przepływu

Wzory używane do obliczeń:

gdzie:

V_śr - prędkość średnia

d - średnica rury

v - współczynnik lepkości kinematycznej

gdzie:

p - zmiana ciśnienia

- gęstość

gdzie:

Q - wydatek

S - pole powierzchni przekroju

gdzie:

- różnica objętości

t - czas przepływu

gdzie

ΔPd - zmiana ciśnienia dynamicznego

Δh -

ρ_cm - gestość cieczy

g - przyśpieszenie ziemskie

k - V_śr/V_max

1

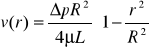
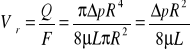
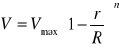
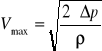
(1/10)

---