Twierdzenie o trzech ciągach

Jeżeli

dla prawie wszystkich n mamy
,

,

to ciąg
jest zbieżny oraz
.

Pokażemy na kilku przykładach, jak w praktyce zastosować powyższe twierdzenie, zwane twierdzeniem o trzech ciągach, do obliczania wybranych granic ciągów liczbowych.

W rachunkach pomoże nam kalkulator ClassPad 300 Plus.

Przykład 1. Obliczyć granicę

Zauważmy, że

zatem

Wobec tego są spełnione założenia twierdzenia o trzech ciągach oraz

Przykład 2. Obliczyć granicę

Zauważmy, że

zatem

Wobec tego są spełnione założenia twierdzenia o trzech ciągach oraz

Przykład 3. Obliczyć granicę

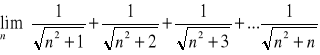
Zauważmy, że

zatem

Wobec tego są spełnione założenia twierdzenia o trzech ciągach oraz

Przykład 4. Obliczyć granicę

Zauważmy, że licznik jest sumą n początkowych wyrazów ciągu arytmetycznego, zatem

Wobec tego

Ponieważ
, więc

Na mocy twierdzenia o trzech ciągach stwierdzamy, że poszukiwana granica istnieje i jest równa 0.

---