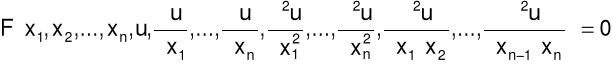
(1)
RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
Równaniem różniczkowym cząstkowym nazywamy równanie różniczkowe, którym występuje funkcja niewiadoma dwóch lub więcej zmiennych i jej pochodne cząstkowe.
Rzędem równania różniczkowego cząstkowego nazywamy najwyższy rząd pochodnej funkcji niewiadomej występującej w danym równaniu.
Równanie różniczkowe cząstkowe rzędu drugiego:
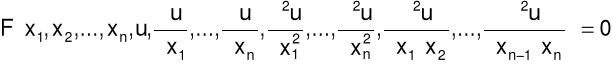
(1)
Rozwiązaniem lub całką równania (1) nazywamy każdą taka funkcję
![]()
(2)
n zmiennych niezależnych x1, x2, …, xn mającą drugie pochodne w pewnym n-wymiarowym obszarze Ω,
która po podstawieniu wraz ze swymi pochodnymi do wyrażenia F w zależności (1), spowoduje,
że wyrażenie F będzie tożsamościowo równe zeru w obszarze Ω.
Rozwiązaniem ogólnym równania różniczkowego cząstkowego nazywamy związek funkcyjny określający klasę rozwiązań.
Zagadnieniem o warunku początkowym (zagadnieniem Cauchy'ego)
nazywamy problem poszukiwania takiego rozwiązania ![]()
równania (1),
które dla pewnej wartości x1=a1 jest równe z góry zadanej funkcji ![]()
n-1 zmiennych x2, x3,…,xn,
tzn. u(a1,x2,x3,…,xn)= ![]()
KLASYFIKACJA RÓWNAŃ LINIOWYCH Z DWIEMA ZMIENNYMI
Równaniem różniczkowym cząstkowym liniowym rzędu drugiego o niewiadomej funkcji u(x,y) dwóch zmiennych niezależnych x i y nazywamy następujące równanie:
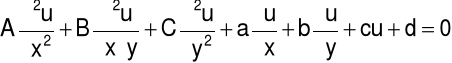
(3)
gdzie A, B, C, a, b, c są danymi funkcjami dwóch zmiennych x i y o ciągłych pochodnych w pewnym obszarze płaskim D,
przy czym ![]()
KLASYFIKACJA
Obliczamy ![]()
Jeżeli ![]()
>0 to równanie (3) nazywamy hiperbolicznym
Jeżeli ![]()
=0 to równanie (3) nazywamy parabolicznym
Jeżeli ![]()
<0 to równanie (3) nazywamy eliptycznym
Z każdym z typów równania (3) jest związana pewna
postać kanoniczna
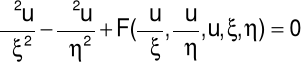
dla ![]()
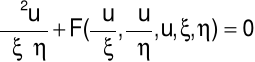
dla ![]()
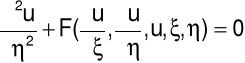
dla ![]()
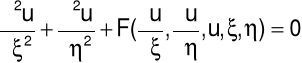
dla ![]()
Można tak dobrać funkcje f i g, by po przejściu do zmiennych
![]()
i ![]()
w równaniu (3) otrzymać jedną z wyżej podanych postaci kanonicznych
Charakterystykami równania (3) nazywamy krzywe całkowe równań różniczkowych zwyczajnych:
![]()
które możemy zapisać w postaci:
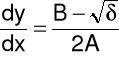
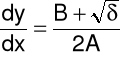
gdy ![]()
lub
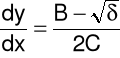
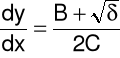
gdy ![]()
Przykład 1.
Sprawdzić, czy funkcja ![]()
jest rozwiązaniem równania:
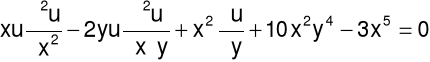
Przykład 2.
Wyznaczyć ogólne rozwiązanie u(x,y) równania
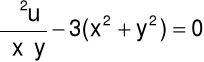
Przykład 3.
Wyznaczyć rozwiązanie u(x,y) równania 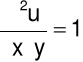
spełniające następujące warunki:
![]()
![]()
Przykład 4.
Sprawdzić typ równania:
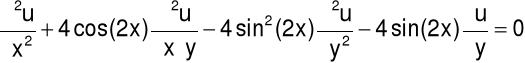
4