Immunizacja portfela obligacji

ryzyko inwestycji w obligacje

inwestycje w obligacje, mimo iż są uważane za dość bezpieczne, nie są pozbawione ryzyka

najważniejsze z nich to:

1. ryzyko niedotrzymania warunków, kredytowe (default risk) - gdy emitent obligacji może nie płacić odsetek od obligacji i / lub nie dokonać wykupu obligacji

najmniejszym ryzykiem tego rodzaju charakteryzują się obligacje skarbowe, największym z kolei obligacje przedsiębiorstw, choć nie w jednakowym stopniu

aby ułatwić decyzje inwestorom stworzono ratingi obligacji (najbardziej renomowane to Standard & Poor's oraz Moody) - poszczególne spółki otrzymują oceny w zależności od szacowanego stopnia ryzyka

obligacje o wyższym ryzyku niedotrzymania warunków oferują wyższe oprocentowanie

2. ryzyko stopy procentowej (interest rate risk) - możliwe jest zrealizowanie z inwestycji innej stopy dochodu niż zakładana, a zmiana ta wynika ze zmiany rynkowej stopy procentowej

wyróżniamy dwa rodzaje ryzyka stopy procentowej:

1. ryzyko zmiany ceny (ryzyko okresu posiadania, price risk, holding period risk) - inwestor decyduje się na wcześniejsza sprzedaż obligacji na rynku wtórnym, z którego cena nie jest wcześniej znana w przeciwieństwie do wartości nominalnej w terminie wykupu obligacji

wzrost stóp procentowych (przy innych warunkach nie zmienionych) powoduje spadek ceny obligacji, a zatem spadek realizowanej stopy dochodu

2. ryzyko reinwestowania (reinvestment risk) - w modelu zakładamy reinwestowanie odsetek po stopie równej YTM

jeśli stopa ta okaże się wyższa (przy pozostałych warunkach niezmienionych), wyższa będzie także realizowana stopa dochodu

obligacje zerokuponowe wolne są tego rodzaju ryzyka (nie wypłacają odsetek)

działanie ryzyka zmiany ceny i ryzyka reinwestycji jest więc przeciwstawne, jednak efekt działania ryzyka zmiany ceny będzie silniejszy, jeśli stopa wypłaty kuponu jest niska, a okres inwestycji stosunkowo krótki

strategie inwestowania w obligacje

zakładamy, że inwestor będzie musiał w przyszłości dokonać pewnych płatności (np. spłaty zobowiązań), należy tak inwestować środki, aby były co do kwoty i terminu zgodne z ujemnymi przepływami pieniężnymi

1. dopasowanie przepływów pieniężnych (cash flow matching)

dla każdego przepływu pieniężnego (począwszy od ostatniego) dopasowuje się kolejne przepływy dodatnie, będące efektami inwestycji w obligacje

podstawowym warunkiem stosowania tej strategii jest duża liczba różnych rodzajów obligacji (zwłaszcza jeśli chodzi o terminy wykupu)

PRZYKŁAD: przepływy ujemne: 1 rok - 100 000

2 rok - 150 000

3 rok - 150 000

4 rok - 200 000

5 rok - 250 000

rodzaje obligacji dostępnych na rynku o wartości nominalnej 100 zł i odsetkach płatnych co roku: jednoroczne zerokuponowe

dwuletnie o oprocentowaniu 7%

trzyletnie o oprocentowaniu 9%

czteroletnie o oprocentowaniu 10%

pięcioletnie o oprocentowaniu 12%

Rodzaj i liczba obligacji	1 rok	2 rok	3 rok	4 rok	5 rok
Roczne - 422	42 200
Dwuletnie - 922	6 454	98 654
Trzyletnie - 986	8 874	8874	107 474
Czteroletnie - 1 575	15 750	15 750	15 750	173 250
Pięcioletnie - 2 233	26 796	26 796	26 796	26 796	250 096
Suma	100 074	150 074	150 020	200 046	250 096
Różnica w dopasowaniu	+74	+74	+20	+46	+96

różnice w dopasowaniu wynikają z tego, iż można kupować jedynie całkowitą liczbę obligacji

po piątym roku z inwestycji w jedną obligację otrzymamy 112 zł

kwota której będziemy potrzebować to 250 000 zł

musimy więc kupić 250 000 / 112 = 2 233 obligacje

po czwartym roku z inwestycji w jedną obligację otrzymamy 110 zł

kwota której będziemy potrzebować to 200 000 zł

należy także uwzględnić kwotę dochodu z obligacji pięcioletnich

2 233 obligacji * 12 zł (kupon) = 26 796 zł

czyli pozostała do zabezpieczenia kwota wynosi 200 000 - 26 796 = 173 204 zł

musimy więc kupić 173 204 / 110 = 1 575 obligacji

po trzecim roku z inwestycji w jedną obligację otrzymamy 109 zł

kwota której będziemy potrzebować to 150 000 zł

należy także uwzględnić kwotę dochodu z obligacji pięcioletnich oraz czteroletnich

1 575 obligacji * 10 zł (kupon) = 15 750 zł

czyli pozostała do zabezpieczenia kwota wynosi 150 000 - 26 796 - 15 750 = 107 454 zł

musimy więc kupić 107 454 / 109 = 986 obligacji

po drugim roku z inwestycji w jedną obligację otrzymamy 107 zł

kwota której będziemy potrzebować to 150 000 zł

należy także uwzględnić kwotę dochodu z obligacji pięcio-, cztero- oraz trzyletnich

986 obligacji * 9 zł (kupon) = 8874 zł

czyli pozostała kwota wynosi 150 000 - 26 796 - 15 750 - 8 874 = 98 580 zł

musimy więc kupić 98 580 / 107 = 922 obligacje

po pierwszym roku z inwestycji w jedną obligację otrzymamy 100 zł

kwota której będziemy potrzebować to 100 000 zł

należy także uwzględnić kwotę dochodu z obligacji pięcio-, cztero-, trzy- oraz dwuletnich

922 obligacji * 7 zł (kupon) = 6 454 zł

czyli pozostała kwota wynosi 100 000 - 26 796 - 15 750 - 8 874 - 6 454 = 42 126 zł

musimy więc kupić 42 126 / 100 = 422 obligacje

2. uodpornienie portfela (portfolio immunization)

czyni portfel obligacji odpornym na ryzyko stopy procentowej (znosi się działanie ryzyka zmiany ceny i ryzyka reinwestowania)

w przypadku jednego ujemnego przepływu, metoda wykorzystuje dwie zasady:

• wartość początkowa inwestycji równa jest zdyskontowanej wartości zobowiązania inwestora (wartość portfela równa wartości bieżącej pożądanej wartości końcowej)

• duracja utworzonego portfela musi być równa długości do terminu płatności zobowiązania inwestora (duracja portfela równa okresowi inwestowania)

PRZYKŁAD: za dwa lata nastąpi ujemny przepływ pieniężny w wysokości 10 000 zł

mamy do dyspozycji obligacje o wartości nominalnej 100 zł i stopie dochodu w terminie do wykupu równej 8%:

• roczne zerokuponowe

• dwuletnie oprocentowane na 9%, odsetki płatne co roku

• trzyletnie oprocentowane na 10%, odsetki płatne co roku

można obliczyć wartości bieżące obligacji oraz duracje:

• roczne - 92.59 - 1

• dwuletnie - 101.78 - 1.92

• trzyletnie - 105.15 - 2.74

zgodnie z drugą zasadą duracja portfela musi wynieść 2

z kolei udziały składników portfela muszą się sumować do jedności

w₁ * 1 + w₂ * 1.92 + w₃ * 2.74 = 2

w₁ + w₂ + w₃ = 1

musimy ustalić wartość jednego z udziałów (np. w₂ = 0.5)

po wyliczeniu otrzymujemy w₁ = 0.19 i w₃ = 0.31

zgodnie z pierwszą zasadą należy zainwestować zdyskontowaną wartość zobowiązania, czyli 10 000 / (1 + 0.08)^2 = 8 573.39 zł

oznacza to, że w celu uzyskania obliczonej wartości początkowej portfela należy zakupić 0.19 * 8 573.39 / 92,59 = 18 obligacji rocznych,

0.50 * 8 573.39 / 101.78 = 43 obligacje dwuletnie,

0.31 * 8 573.39 / 105.15 = 26 obligacji trzyletnich

wówczas wartość początkowa portfela wynosi:

18 * 92.59 + 43 * 101.78 + 26 * 105.15 = 8 570.13 zł

a końcowa (po dwóch latach):

18 * 92.59 * (1.08) + 43 * 101.78 * (1.08)^2 + 26 * 105.15 * (1.08)^3 = 10348.7 zł

taki portfel odporny jest na ryzyko stopy procentowej, ale tylko wówczas, gdy zmiany stopy są takie same dla wszystkich obligacji

model zakłada stałą krzywą stóp procentowych, a w rzeczywistości może ona przybierać różne kształty, co powoduje wystąpienie ryzyka przy uodpornieniu portfela

ryzyko to może zostać zmniejszone przez skoncentrowanie dużych wartości dochodów stosunkowo blisko okresu inwestowania

do pomiaru ryzyka uodpornienia portfela stosuje się miarę zaproponowaną przez Fonga i Vasica:

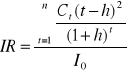
IR - ryzyko uodpornienia

h - okres, będący horyzontem inwestowania

I₀ - inwestycja początkowa

zerowe ryzyko będzie występowało, gdy portfel będzie zawierał obligacje zerokuponowe o terminie wykupu takim samym jak okres inwestowania

1

5

---