Grupa 6 ZADANIA Z ALGEBRY (na 14 marca)

1. Rozważmy grupę, w której dla każdego jej elementu g zachodzi
. Proszę

udowodnić, że ta grupa musi być abelowa (czyli że jej mnożenie musi być przemienne).

W: Proszę zbadać „kwadrat” elementu
, gdzie
i
są dwoma dowolnymi

elementami rozważanej grupy.

2. Proszę dowieść równości:
zachodzącej dla dowolnych liczb zespolonych
,
. Pionowymi kreskami opisany jest moduł liczby zespolonej, czyli
.

Jaka jest geometryczna interpretacja dowodzonej równości?

3. Proszę obliczyć moduły i fazy następujących dwóch liczb zespolonych:

a. , b. .

4. Proszę dowieść, że .

5. Proszę znaleźć moduł i fazę liczby zespolonej .

Wskazówka: Przydają się kąty połówkowe i wzór de Moivre'a.

6. Pierwiastkiem kwadratowym z liczby
nazywamy każdą liczbę zespoloną
, która podniesiona do kwadratu daje
. Mamy więc
. Jest to równanie, w którym niewiadomymi są dwie liczby rzeczywiste
i
. Każda znaleziona para liczb
i
daje nam kolejny znaleziony pierwiastek kwadratowy z liczby
.

Obliczamy kwadrat
Równość dwóch liczb zespolonych polega na tym, że równe są ich części - odpowiednio - rzeczywiste i urojone. Tak więc musi zachodzić

,
.

Proszę pokazać, że ten układ równań ma dwa rozwiązania, czyli że istnieją dwa pierwiastki kwadratowe z liczby
:

.

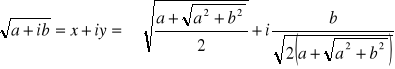
7. Wykorzystując wynik zadania 6 do wyliczenia pierwiastka z wyróżnika, proszę rozwiązać równanie kwadratowe
.

---