1.Wprowadzenie .

Celem ćwiczenia jest sprawdzenie stateczności istniejącej skarpy po jej obciążeniu metodą Felleniusa. Skarpa jest bardzo często spotykanym w budownictwie obiektem z ziemi, a stateczność nasypu ważnym problemem rozstrzyganym w mechanice gruntów. Od prawidłowo zaprojektowanego nasypu zależy wiele rzeczy, a strata stateczności osuwiska pod działaniem obciążenia może doprowadzić do wielu awarii i wypadków. W naszym przypadku rozważamy skarpę złożoną z gruntu zarówno spoistego jak i niespoistego bez zwierciadła wody , obciążonego jakaś równomiernie rozłożoną siłą - obiektem budowlanym. Przy obliczaniu skarpy korzystamy z metoy Felleniusa wspierając się normą PN-81/B03020.

2.Charakterystyka projektowanego obiektu .

Analizowanym obiektem jest skarpa o wymiarach 28m x 14m, wykonana na zboczu górskim. U podstawy skarpy przewiduje się wykonanie nawierzchni utwardzonej, która nie powinna być zagrożona osuwaniem się skarpy. Skarpa obciążona jest obciążeniem równomiernie rozłożonym w postaci jezdni przeznaczonej pod ruch samochodowy.

3.Charakterystyka geotechniczna podłoża .

Układ oraz miąższość warstw określono na podstawie wierceń w terenie. Nazwę gruntu określono w terenie metodą makroskopową (bezpośrednią), a wskaźniki testowe za pomocą sondowania.

Przekrój pionowy zalegających warstw gruntu przedstawiono na rys nr 1, zadane warunki gruntowe zebrano w tabeli nr 1.

2.0 9.0m

1 Ip 5.0 m

2 Po 4.0 m

3 Gp 3.0 m

4 p_p

2.0 m

rys 1

tabela nr 1

GRUNT	IL	ID	Sr	ρ	u	cu
				[g/cm^3]	[ ^o]	[kPa]
Ił pylasty	0,0	-	---	1,80	13	60
Pospółka	-	0,57	mw	2,15	39	0
Glina pylasta	<0	-	---	2,05	22	40
Ił piaszczysty	0,04	-	---	2,00	24,3	57

4.Sprawdzenie stateczności skarpy metodą Felleniusa .

4.1. Wprowadzenie.

Analizujemy równowagę bryły klina odłamu ograniczonego od góry koroną , a od dołu potencjalną cylindryczną powierzchnią odłamu. Powierzchnia taka podzielona jest na bloki o grubości nie mniejszej od 1/10 szerokości bryły i o pionowych ścianach bocznych. Bloki takie dzieli się na pomniejsze bryły ze względu na rodzaj gruntu tak aby można było obliczyć pole oraz kąt nachylenia i-tego bloku. Dzieląc tak bloki a następnie sumując wyniki ciężarów i ich składowych normalnych oraz stycznych a także siły oporu tarcia i kohezji gruntu otrzymujemy wynik stateczności skarpy.

4.2. Założenia do metody.

1. Płaski stan naprężenia.

2. Występowanie jednocześnie w całej powierzchni poślizgu stanu granicznego według hipotezy Coulomba - Mohra.

3. Niezmienność parametrów wytrzymałościowych ϕ_ui i c_ui w czasie.

4. Jednakowe przemieszczenia wzdłuż całej powierzchni poślizgu ( oznacza to , że każdy odłam jest bryłą sztywną ).

5. W podstawie każdego bloku przyjmuje się grunt o jednakowych parametrach.

6. Przyjmuje się brak sił bocznych ( są pomijane jako siły wewnętrzne ).

7. Powierzchnia poślizgu przechodzi przez dolną krawędź skarpy.

4.3. Tok postępowania.

Na wstępie chciałbym zaznaczyć , że opis ten będzie dotyczył skarpy , w której nie ma wody. Wyznacza się na początku prostą najniebezpieczniejszych osi obrotu poprzez znalezienie dwóch punktów. Po znalezieniu prostej następnie trzeba narysować trzy możliwe powierzchnię poślizgu. Pierwsza winna znaleźć się przed obciążeniem , druga przy końcu obciążenia od strony płaskiego terenu , trzecia za obciążeniem. Wykonuje się trzy takie schematy dla obliczenia , najmniejszego współczynnika pewności , najbardziej niebezpieczną pow. poślizgu za pomocą równania paraboli. Krokiem następnym jest podział na bloki tak aby poszczególne rodzaje gruntów dzieliły bloki na trójkąty i kwadraty , może wystąpić trapez , ale tylko taki który nie jest podzielony przez dwa rodzaje gruntu. Następnie przeprowadza się obliczenia według poniżej przedstawionych wzorów:

W_i - ciężar bloku

N_i - składowa normalna siły W_i

B_i - składowa styczna siły W_i

T_i - siła oporu tarcia

G_i - ciężar bloku bez uwzględnienia obciążenia zewnętrznego

Wyznacza się , po obliczeniu dla każdego bloku wszystkich sił , momenty obracające bryłę i utrzymujące bryłę względem tego samego środka O:

R - promień okręgu

Stosunek tych dwóch wielkości da wskaźnik stateczności.

a) Według Wiłuna

=

b) Według Rosińskiego

Siły obracające ujemne są zaliczane do sił utrzymujących.

F=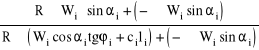

4.4.Wyznaczenie najniebezpieczniejszej powierzchni poślizgu.

Odczytuję z rysunku odległości poszczególnych środków względem

pierwszego środka:

x₁ = 0 m F₁ = 1,99

x₂ = 7,3 m F₂ = 1,79

x₃ = 16,5 m F₃ = 1,82

Z równania drugiego stopnia (F(x) = ax² + bx + c ), po podstawiam wyżej podanych

wartości, obliczam a , b , c :

a = 0,0019

b = -0,0410

c = 1,99

Podstawiam znowu wartości do równania , aby je zróżniczkować:

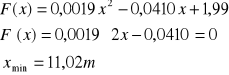
Do obliczenia F_min podstawiam po raz kolejny wartości , tym razem x_min , do równania drugiego stopnia: F_min = 1,76

5.Uwagi końcowe .

Wartość F_dop przy zastosowaniu metody Felleniusa dla skarp stałych (t>5lat) przyjmuje się w granicach 1,5 do 2,0. Jak widać: F_min >F_dop Więc skarpa jest stateczna.

---