PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA INSTYTUT POLITECHNICZNY
2004/2005	LABORATORIUM Z AUTOMATYKI I STEROWANIA
Ćwiczenie nr 4	UKŁADY KOMBINACYJNE
Budowa i Eksploatacja Maszyn ST. Zaoczne Semestr III	Dyksik Arnold Stefaniak Łukasz Kania Mateusz
Data wykonania		Data	Ocena	Podpis
2005-04-04	T
	S

1. Cel ćwiczenia

Celem ćwiczenia była zapoznanie się z układami kombinacyjnymi oraz poznanie typowych bramek używanych w technice cyfrowej (AND, NOR, NOT, EX-OR, OR, XOR).

2. Wiadomości wstępne

Bramka Ex-OR (XOR, ALBO) (ang. Exclusive OR - LUB z wyłączeniem) realizuje funkcje
która jest także nazywana sumą modulo 2

a	b
0	0	0
0	1	1
1	0	1
1	1	0

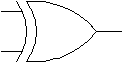
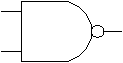
Bramka NAND jest funkcjonalnie pełna, bowiem stosując ją można zrealizować operację iloczynu logicznego AND, jak i operację negacji NOT - czyli zgodnie z wcześniejszymi wnioskami dowolną funkcję logiczną.

a	b
0	0	1
0	1	1
1	0	1
1	1	0

Bramka OR
Wyjście bramki OR (czyli LUB) jest w stanie wysokim, jeżeli któreś z wejść (lub oba) jest w stanie wysokim. Można to wyrazić za pomocą "tablicy prawdy", pokazanej na rysunku 8.2. Narysowana bramka to 2-wejściowa bramka OR. W przypadku ogólnym bramki mogą mieć dowolną liczbę wejść, ale typowy układ scalony zawiera zwykle cztery bramki 2-wejściowe, trzy bramki 3-wejściowe lub dwie bramki 4-wejściowe. Na przykład wyjście 4-wejściowej bramki OR będzie w stanie wysokim, jeżeli przynajmniej jedno jej wejście będzie w stanie wysokim.

W algebrze Boole'a symbolowi OR odpowiada symbol +. "A LUB B" zapisywane jest jako A+B.

Bramka AND.
Wyjście bramki AND (czyli I) jest w stanie wysokim tylko wtedy, gdy oba wejścia są w stanie wysokim. Symbol logiczny tej bramki i tablicę prawdy pokazano na rysunku 8.3. Podobnie jak w przypadku bramek OR, dostępne są bramki AND 3- i 4-wejściowe (czasem o większej liczbie wejść). Na przykład 8-wejściowa bramka AND będzie miała wyjście w stanie wysokim tylko wtedy, gdy wszystkie wejścia będą w stanie wysokim.

Rys. 8.3.

W algebrze Boole'a symbolowi AND odpowiada kropka (·). Może być ona pominięta, co jest powszechnie spotykane. "A I B" jest zapisywane jako A · B lub po prostu AB.

Inwerter (funkcja NOT). Często potrzebujemy zmienić stan logiczny na przeciwny (nazywa się to również negowaniem stanu logicznego). Jest to funkcja inwertera, "bramki" o jednym wejściu (rys. 8.4). Boole'owskim odpowiednikiem symbolu NOT (negacji) jest kreska pozioma stawiana nad negowanym elementem, a czasem apostrof ('). "NIE A" jest zapisywane jako A'. Dla wygody składających teksty na oznaczenie

Rys. 8.4.

negacji często zamiast kreski stosuje się symbole /, *, -, '. Tak więc, "NIE A" może być zapisane również następująco: A', -A, *A, /A, A*, A/. W danej publikacji wybiera się zazwyczaj jeden z wymienionych sposobów negacji i konsekwentnie się go stosuje w całym tekście. W naszej używamy notacji A'.

Bramka NOR

Bramka realizuje funkcje logiczną: NOR, NIE SUMA - negacja sumy
Bramka jest złożona z bramki NOT i OR. Zasada działania jest taka sama jak bramki OR z tą różnicą, że sygnał wyjściowy jest jeszcze negowany.
Bramka ta stanowi SYSTEM FUNKCJONALNIE PEŁNY, czyli za jej pomocą można przedstawić każdą złożoną funkcję logiczną.

Tablica prawdy:

IN 1	IN 2	OUT
0 0 1 1	0 1 0 1	1 0 0 0

3. Przebieg ćwiczenia

Bramka AND (układ scalony UCY 7400)

A, B - sygnał wejściowy

Y - sygnał wyjściowy

A	B	Y
1	1	0
0	1	1
0	0	1
1	0	1

Bramka AND (układ scalony UCY 7408)

A, B - sygnał wejściowy

Y - sygnał wyjściowy

A	B	Y
1	1	1
0	1	0
0	0	0
1	0	0

Bramka NOR

A, B - sygnał wejściowy

Y - sygnał wyjściowy

A	B	Y
1	0	0
0	0	1
0	1	0
1	1	0

Inwerter (funkcja NOT)

A - sygnał wejściowy

Y - sygnał wyjściowy

A	Y
0	1
1	0

Układ kombinacyjny złożony z bramek EX - OR

A, B, C, D - sygnały wejściowe

Y - sygnał wejściowy

A	B	C	D	Y
0	0	0	0	0
1	0	0	0	1
1	1	0	0	0
1	1	1	0	1
1	1	1	1	0
0	1	1	1	1
0	0	1	1	0
0	0	0	1	1
0	0	0	0	0
0	1	1	0	0
1	0	0	1	0
1	1	1	0	0
0	1	0	1	0
0	1	0	0	1
0	0	1	0	1

4. Wnioski

Podczas tego ćwiczenia zapoznaliśmy się z podstawowymi bramki stosowanymi w technice cyfrowej, wyniki otrzymane podczas ćwiczenia pokrywają się z teorią.

Innym typowym zadaniem układów cyfrowych jest pobranie pewnych liczb binarnych i ich wyświetlenie, wydrukowanie lub jako znaków dziesiętnych. We wszystkich wymienionych zadaniach sygnały (stany) wyjściowe są zdeterminowanymi funkcjami sygnałów (stanów) wejściowych. Zalicza się je do zadań "kombinacyjnych". Wszystkie mogą być wykonane za pomocą urządzeń zwanych bramkami, które realizują działania algebry Boole`a w dziedzinie układów dwustanowych (binarnych).

---