POLE GRAWITACYJNE, Zagadnienia:

1. Prawo powszechnego ciążenia

2. Prawa Keplera

3. Ruch ciał w polu grawitacyjnym, prędkość na orbicie.

4. Energia potencjalna grawitacji.

5. I i II prędkość kosmiczna. Stan przeciążenia i nieważkości.

6. Graficzny obraz pola grawitacyjnego.

Przykładowe zadania (źródłem zadań są różne zbiory dla szkół ponadgimnazjalnych):

1. Masa Marsa jest około 10 razy mniejsza od masy Ziemi, a jego promień jest około 2 razy mniejszy od promienia Ziemi. Ile wynosi stosunek ciężaru dowolnego ciała na powierzchni Ziemi do ciężaru tego ciała na powierzchni Marsa?

2. Oblicz siłę grawitacji z jaką Marek (50 kg) przyciąga Michała (40kg) jeżeli chłopcy znajdują się w odległości 4m. Porównaj obliczoną siłę z siłą z jaką Ziemia przyciąga Michała. Jak zmieni się siła oddziaływania między chłopcami gdy odległość między nimi wzrośnie dwukrotnie?

3. Człowiek na powierzchni Ziemi waży 600 N. Ile ważyłby ten człowiek na planecie o dwukrotnie większej masie i takim jak Ziemia promieniu?

4. W jakiej odległości od powierzchni Ziemi przyspieszenie ziemskie wynosi g = 1 m/s². (R_z = 6370 km, g_z = 9,8 m/s².

5. Ile waży (czyli z jaką siłą grawitacji jest przyciągane) ciało o masie m = 150 kg na powierzchni Księżyca? Promień Księżyca jest 11/3 razy mniejszy od promienia Ziemi, masa Księżyca jest 81 razy mniejsza od masy Ziemi.

6. Jaką gęstość powinna mieć substancja, z której wykonano dwie kule o promieniu 1m przyciągające się grawitacyjnie z odległości 10 m (odległość między środkami kul) silą 66,7 μN.

7. Oblicz wypadkową siłę działającą na kulę A (m=2kg) ze strony kuli B(m=1kg) i kuli C(m=2kg). Kule znajdują się na jednej prostej, odległość kuli B od kuli C wynosi 10m, pomiędzy nimi w odległości 4m od kuli B znajduje się kula A. Przedstaw siły działające na kulę A na rysunku.

8. Oblicz energia potencjalna ciała o masie m₁=20 ton umieszczonego w odległości 5630km od powierzchni Ziemi? Promień Ziemi 6370 km.

9. Oblicz masę planetoidy, dla której II prędkość kosmiczna wynosi 36,52 m/s, a promień 1000 km.

10. Okres obiegu planety Neptun po orbicie okołosłonecznej wynosi 165 lat. Oblicz w jednostkach astronomicznych (AU) średnią odległość Neptuna od Słońca.

11. Oblicz przyspieszenie grawitacyjne ciała na Merkurym, Jowiszu (masa i promień podane są w tabeli w podręczniku). Oblicz wartości I i II prędkości tych planet.

12. Oblicz okres obiegu Wenus i Merkurego wokół Słońca. (potrzebne dane są w tabeli w podręczniku)

13. Oblicz prędkość z jaką porusza się księżyc Saturna. Przyjmij, że księżyc porusza się po orbicie kołowej. Promień orbity księżyca wynosi 2,95·10⁵ km, okres obiegu 1,9 dnia. Na podstawie tych danych oblicz masę Saturna..

14. Oblicz prędkość, z jaką Ziemia obiega Słońce. (promień orbity 1,5·10⁸ km, masa Słońca 2·10³⁰ kg).

15. Galileusz jako pierwszy zaobserwował cztery księżyce Jowisza i wyznaczył ich okres obiegu wokół tej planety. Obecnie wiemy też jakie są promienie ich orbit. Uzupełnij tabelę

Nazwa Księżyca	Okres obiegu	Promień orbity
Io		422000 km
Europa	3,55118dni
Ganimedes	7,15455dni	1070000km
Kallisto		1883000 km

16. Satelita o masie 1500 kg zostaje wyniesiony z powierzchni Ziemi na orbitę kołową i krąży w odległości 1000 km od powierzchni Ziemi (Promień Ziemi 6370 km). Oblicz prędkość liniową i okres obiegu satelity wokół Ziemi na danej orbicie.

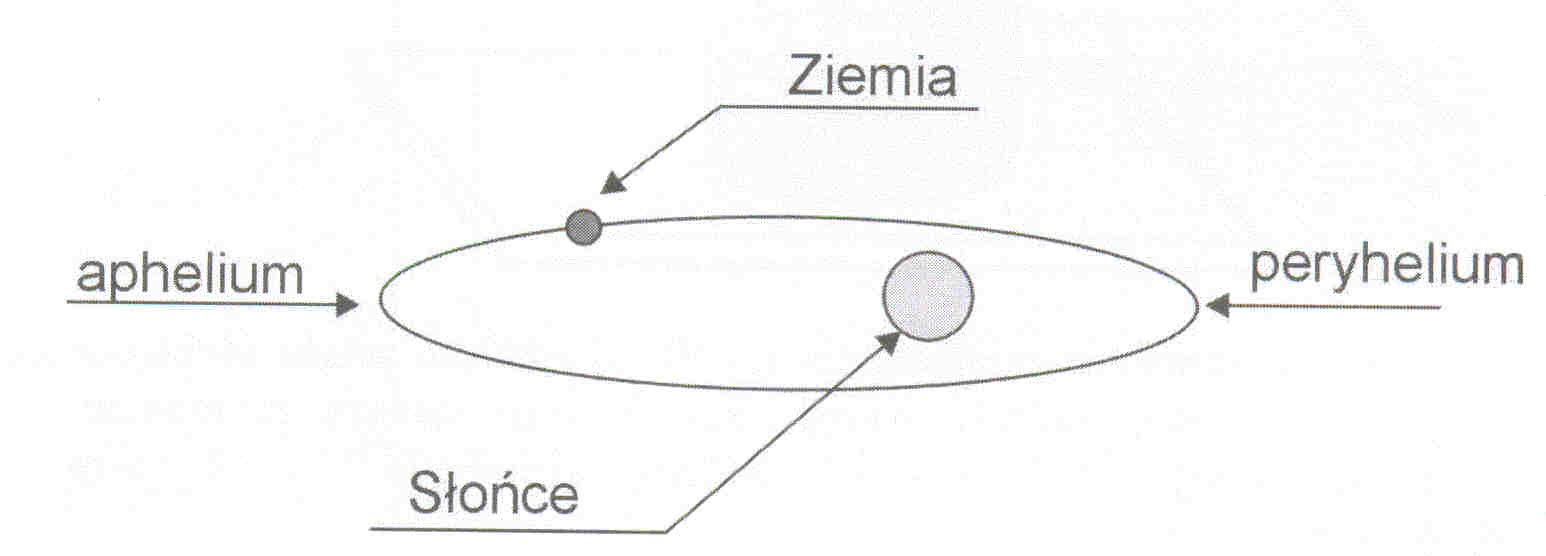
17. Ziemia, podczas ruchu wokół Słońca po eliptycznej orbicie, raz znajduje się najbliżej Słońca(peryhelium), a raz najdalej (aphelium). Zapisz, w którym punkcie orbity wartość prędkości liniowej Ziemi jest największa, a w którym najmniej sza? Uzasadnij odpowiedź.

---