- Zadanie interpolacji polega na znalezieniu funkcji L, zwanej funkcją interpolującą , która w węzłach xi , i = 0, 1, ... ,n , pokrywa się z funkcją f (interpolowaną)

L_n(xi) = f(xi) dla i = 0, 1, ... , n .

------------------------------------------------------------------------------------------------------------------

TWIERDZENIE. Zadanie interpolacyjne Lagrange'a na jednoznaczne rozwiązanie, czyli istnieje tylko jeden wielomian spełniający powyższy warunek.

DOWÓD. Szukany wielomian zapiszemy w postaci

Zadanie interpolacji -> Ln(xi) = yi dla i = 0, 1, ... ,n

prowadzi do układu n+1 równań liniowych Va = y

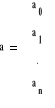
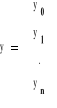
Macierz Vandermonde'a jest macierzą nieosobliwą dla układu różnych węzłów. Zatem układ Va = y ma dokładnie jedno rozwiązanie. Istnieje wielomian postaci (**) i jest on wyznaczony jednoznacznie.

Postać Lagrange'a dla n =2 (3 węzły)

Newtona dla n =2 (3 węzły)

Iloraz różnicowy- wielkość charakteryzująca przyrost funkcji na danym przedziale.

Wyrażenia

1-go rzę du

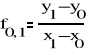
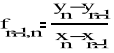
2-go rzę du

,

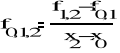
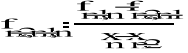
rzędu k

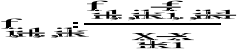
Niech w przedziale [a,b] danych będzie (n+1) punktów x0, x1, ... , xn , przy czym

a = x0 < x1 < ... < x n-1 < xn = b.

Funkcję s(x) określoną na przedziale [a,b] nazywamy funkcją sklejaną stopnia m , jeżeli

1) s(x) jest wielomianem stopnia co najwyżej m na każ dym podprzedziale (xi , xi+1) , i = 0,1,... , n-1

2) s(x) jest funkcją klasy C(m-1) ([a,b]) .

Zbiór wszystkich funkcji sklejanych stopnia m o węzłach xi ( i = 0,1,...,n) oznaczymy Sm .

Funkcja sklejana stopnia m zależ y od n (m+1) - m (n-1) = n+m parametrów.

Funkcję s(x) z Sm nazywamy interpolacyjną funkcją sklejaną stopnia m dla funkcji f , jeżeli

s(xi) = yi , i = 0,1,...,n

Dla m > 1 interpolacyjna funkcja sklejana zależ y od (m-1)

parametrów i należ y na nią nałożyć dodatkowe warunki.

Interpolacyjna

funkcja sklejana stopnia trzeciego zależ y od dwóch parametrów, wobec czego nakładamy na nią

dwa dodatkowe warunki. Warunki te najczęściej nakładamy w węzłach krańcowych a i b.

Np. mogą mieć one postać

s'(a + 0) =(alfa) oraz s'(b - 0) =(beta)

gdzie (alfa),(beta) są ustalonymi liczbami rzeczywistymi. Jeżeli funkcja f ma pochodne w punktach a i b

oraz znamy ich wartości, to możemy je przyją ć jako liczby występują ce po prawych stronach powyższych warunków. Natomiast, jeżeli znamy tylko wartości funkcji f w węzłach - mogą to

być przybliżenia pochodnych.

TWIERDZENIE. Istnieje dokładnie jedna interpolacyjna funkcja sklejana stopnia trzeciego

spełniają ca podane wyż ej dodatkowe warunki.

w przypadku wę zł ów równoodległ ych

(x_i pokazuje nam maximum równe n) xi = x0 +ih, h = (b-a)/n , i = 0,1, ... ,n

Okreś lamy (n+3) funkcje i =i(x) , i = -1, 0, 1, ... , n , n+1 , które stanowią bazę przestrzeni

funkcji sklejanych trzeciego stopnia S3

W przybliżeniach interpolacyjnych przyjmuje się że funkcja przybliżająca L w punktach x_i pokrywa się z wartościami funkcji f natomiast w aproksymacja jest zagadnieniem bardziej ogólnym. Warunek aby funkcja przybliżana i funkcja przybliżająca nie muszą przyjmować dokładnie tych samych wartości w punktach x₁.

Przyjmujemy, ż e funkcja przybliżająca F jest okreś ona przez zależność

F(x) = F(x; a0, a1, .... , am)

od (m+1) parametrów a0, a1, ... , am , przy czym

Ogólnie , zagadnienie aproksymacji na zbiorze punktów X = {x0, x1, ... , xn } polega na

wyznaczeniu parametrów a0, a1, ... , am tak, aby odległości yi (i = 0,1, ... ,n) od F były

minimalne. Sposób wyznaczania parametrów zależy od tego , jak rozumiemy to kryterium. Interpolacja jest jedną z metod aproksymacji - nazywana jest

czę sto aproksymacją interpolacyjną .

W metodzie średniokwadratowej dyskretnej (najmniejszych kwadratów) współczynniki a_j dobieramy tak aby odchylenie średniokwadratowe miało najmniejszą wartość.

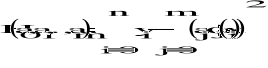
Funkcję F_m(xi) (ta suma z m na górze ) dla której H osiąga minimum nazywamy m-tą funkcją optymalną.

Pochodna z H po a_k k=0,1, …, m otrzymane równości tworzą układ (m+1) równań liniowych z (m+1) niewiadomymi a0, a1, ... , am , zwany układem równań normalnych.

Ga = b, gdzie G = [Gi,j] (i,j = 0,1, ... , m) , a = [a0, a1, ... , am ]T, b = [b0, b1, ... , bm ]T ,

,
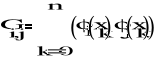
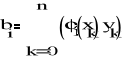
(i,j = 0,1, ... , m).

Macierz G, zwana macierzą Grama, jest macierzą kwadratową stopnia (m+1).

Moż na zapisać

G = MTM i b = MTy,

gdzie y = [y0, y1, ... , yn ]T i

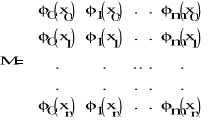
Uwaga. Macierz G jest nieosobliwa wtedy i tylko wtedy, gdy rzą d macierzy M

jest równy (m+1).

Stą d wynika, ż e

Twierdzenie. Jeż eli rzą d macierzy M jest równy (m+1), to istnieje dokł adnie jedna m-ta

funkcja optymalna (w sensie aproksymacji ś redniokwadratowej dyskretnej).

Bł ą d ś redniokwadratowy oblicza się ze wzoru

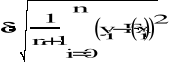
Jeż eli funkcje
są wielomianami stopnia j (j = 0, 1, 2 , ... , m), to Fm jest wielomianem stopnia

co najwyż ej m. Wtedy funkcję optymalną Fm nazywamy m-tym wielomianem (algebraicznym)

optymalnym.

W przypadku jednomianów
, już dla niedużych m (m>5) ukł ad równań normalnych

jest źle lub bardzo źle uwarunkowany. W przypadku przybliż eń wielomianowych z wyją tkiem ,

gdy m jest bardzo małe, nie należ y stosować takiego wyboru funkcji
. Należ y stosować

tzw. wielomiany Grama;

W zagadnieniach aproksymacji często spotykamy się z przypadkiem, gdy yi są wartościami

pomiarowymi pewnego zjawiska , o którym wiadomo, ż e ma przebieg okresowy. Wtedy

do aproksymacji korzystniej jest stosować wielomiany trygonometryczne, a nie algebraiczne.