IV Wojewódzki Konkurs Matematyczny
dla uczniów gimnazjum
eliminacje szkolne 2003/2004
Należy wybrać i rozwiązać 5 spośród 6 podanych zadań.
Warunkiem zakwalifikowania się do etapu rejonowego jest uzyskanie co najmniej 95% punktów.
Czas na rozwiązanie 90 minut.
Zadanie 1.
Czy z odcinków o długościach:
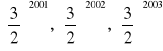
można zbudować trójkąt? Odpowiedź uzasadnij.
Zadanie 2.
Wykaż, że dla dowolnych a, b, c, d ∈ R
![]()
.
Zadanie 3.
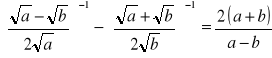
Sprawdź, czy podana równość jest prawdziwa.
Zadanie 4.
Dla jakiej wartości b funkcja: ![]()
ma dokładnie jeden punkt wspólny z kwadratem o przekątnej BD, gdzie: B = ( 2, -2 ) i D = ( -2, 2 )?
Zadanie 5.
Jaką co najmniej średnicę musi mieć garnek, aby można było w nim ustawić obok siebie cztery jednakowe słoiki o promieniu 4 cm?
Zadanie 6.
Towar kosztował x zł. Jego cenę dwukrotnie obniżono o p%. Oblicz końcową cenę tego towaru.
Życzymy powodzenia !
Hanna Kozłowska, Katarzyna Matuszek, Antonina Wiącek
Gimnazjum nr 27 z Oddziałami Integracyjnymi w Poznaniu
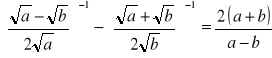
Wyszukiwarka
Podobne podstrony:
2983
2983
2983, Scenariusze Jasełek
2983 001
2983 001 (2)
2983
więcej podobnych podstron