Całkowani przez podstawianie

Tw. Jeżeli f(x) jest ciągła w (a,b) i … jest ciągła w … i istnieje ciągła … to zachodzi wzór

Należy przy tym pamiętać, że podstawienie ma całkę upraszczać

Np.

1. Metoda tożsamościowego przekształcenia

a)

2. Metoda przez podstawienie:

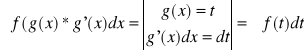
a)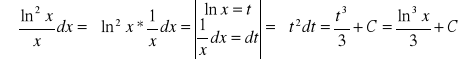

b)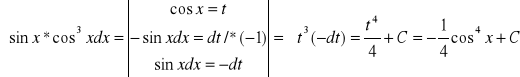

c)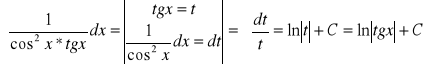

d)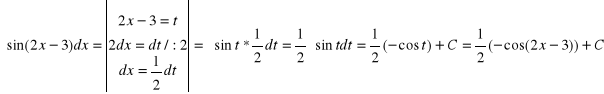

w tym przykładzie można obliczyć całkę bez podstawiania korzystając ze wzoru:

Jeżeli

Wówczas

3. Jeżeli mamy
to można korzystać ze wzoru:

nie wykorzystując za każdym razem podstawienia za f(x) np.

4.

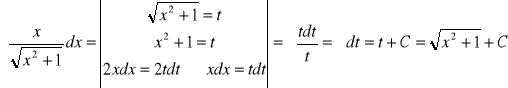
Do wyniku tego dojdziemy też ze wzoru

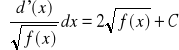
Mamy

Całkowanie przez części

Tw. Jeżeli funkcje
i
mają ciągłe pochodne w X to zachodzi wzór

Dowód: Obliczamy pochodne obydwu stron

L:

P:

Stąd wynika L=P

Przykład

1. 
   
   

2. 
   
   

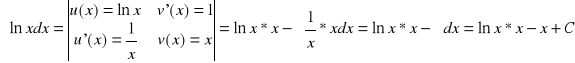
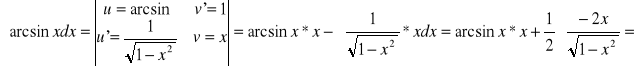
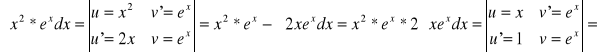
Czasami obliczenie całki będzie łączyć te dwie metody jednocześnie:

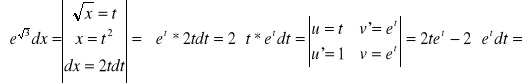
Są przykłady gdzie stosowanie metody całkowania przez części przerywamy w momencie gdy wrócimy do całki wyjściowej np.:

;
;
;

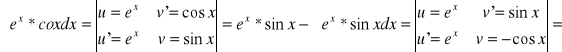
mgr Barbara Pakleza Matematyka 23.02.08

Wykład 1

- 1 -