1. Sformułować twierdzenie o ciągu monotonicznym. Korzystając z niego uzasadnić zbieżność ciągu:
.

2. Podać definicję ciągłości funkcji w punkcie. Obliczyć wartość funkcji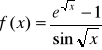
w punkcie x₀ tak aby funkcja f była ciągła w tym punkcie.

3. Wyznaczyć równanie różniczkowe liniowe jednorodne o stałych współczynnikach możliwie najniższego rzędu, jeżeli liczby λ₁=i λ₂=0 są pierwiastkami wielomianu charakterystycznego tego równania. Podać rozwiązanie ogólne, fundamentalny układ rozwiązań oraz sprawdzić liniową niezależność funkcji tego układu.

4. Zbadać zbieżność warunkową i bezwzględną szeregu
.

5. Napisać równanie stycznej do wykresu funkcji f(x)=cos(arctg(lnx)) w punkcie (1,f(1)).

6. Rozwiązać równanie
.

1. Wykazać, że ciąg o wyrazach ujemnych nie może być zbieżny do liczby dodatniej. Obliczyć granicę ciągu
.

2. Sformułować twierdzenie o wartości średniej (Lagrange'a). Korzystając z niego uzasadnić nierówność:
.

3. Wyznaczyć równanie różniczkowe liniowe jednorodne o stałych współczynnikach możliwie najniższego rzędu, jeżeli wiadomo, że funkcje
są rozwiązaniami tego równania. Znaleźć rozwiązanie szczególne spełniające warunki początkowe
.

4. Zbadać zbieżność warunkową i bezwzględną szeregu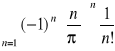
.

5. Wyznaczyć wszystkie asymptoty funkcji f(x)=xarctgx.

6. Rozwiązać równanie