Metody numeryczne - laboratoria 7 (Rozwiązywanie układów równań liniowych - metody dokładne)

1. Problem - rozwiązać układ równań

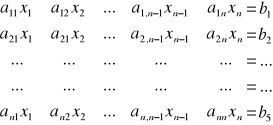
2. Układ zapisany w postaci macierzowej:

Ax = b

3. Proste warianty - z macierzą trójkątna dolną i trójkątną górną

1. z macierzą trójkątną dolną

x₁=b₁/l₁₁

x_i=(b_i-
)/l_ii i = 2…n

2. z macierzą trójkątną górną

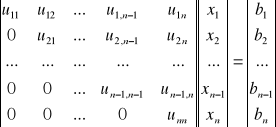
x_n=b_n/u_nn

x_i=(b_i-
)/u_ii i = n-1…1

Koszt obliczenia wartości x_i - kwadratowy (O(n²))

4. Metoda eliminacji Gaussa - zalgorytmizowana typowa metoda rozwiązywania równań liniowych za pomocą dodawania i odejmowania równań, oraz mnożenia równań przez pewną stałą.

l_i1 = a_i1/a₁₁, a₁₁ ≠ 0

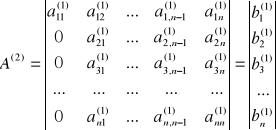
l_i2 = a_i2/a₂₂, a₂₂ ≠ 0

Algorytm:

Dla k = 1…n-1

Dla i = k + 1 …n

l_ik = a_ik^(k)/a_kk^(k), a_ij^(k+1)=a_ij^(k) - l_ika_kj^(k) dla j = k…n

b_i^(k+1) = b_i­^(k) - l_ikb_k^(k)

Złożoność algorytmu rzędu n³ (O(n³))

Otrzymujemy macierz trójkątną górną - którą rozwiązujemy z wykorzystaniem wcześniej przedstawionych metod.

5. Rozkład LU macierzy

Każdy krok rozkładu Gaussa można przedstawić jako iloczyn macierzy:

A^(k+1) = L^(k) A^(k)

U = A⁽ⁿ⁾ = L^(n-1)A^(n-1) = L^(n-1)…L⁽¹⁾ A, stąd

A = (L⁽¹⁾)^-1…(L^(n-1))^-1U

(odwracanie macierzy L⁽ⁱ⁾ - zmienia się tylko znak elementów l_ij na przeciwny)

L = (L⁽¹⁾)^-1…(L^(n-1))^-1U

A = LU

Wtedy rozwiązanie układu równań można wykonać:

LUx = b ->

Ly = b i Ux = y

(oczywiście L - jest trójkątna dolna, U - trójkątna górna)

W przypadku, gdy w przypadku serii równań zmienia się tylko wektor b, warto używać rozkładu LU - bo po pojedynczym wykonaniu rozkładu za każdym razem mamy tylko do rozwiązania 2 razy macierz trójkątną (złożoność kwadratowa).

6. Wybór elementu głównego

Eliminacja Gaussa w najprostszym wariancie nie zawsze działa - przykład - macierz:

a₁₁ = 0 (dzielenie przez 0!)

poza tym - nie zawsze najlepsze własności numeryczne, zwykle zależy nam na tym by dzielić przez największą co do modułu liczbę.

1. wybór częściowy elementu głównego

W każdym kroku algorytmu wyszukujemy element największy (co do modułu) w aktualnie przetwarzanej kolumnie (kolumnie k - dla ustalenia uwagi, w zasadzie tylko w dół od elementu a_kk włącznie):

i zamieniamy wierszy k i p w macierzy A, oraz w wektorze b

(odpowiada to zmianie kolejności równań w układzie równań)

2. pełny wybór elementu głównego

Różni się od wyboru częściowego tym, że elementu poszukujemy we fragmencie macierzy w dół i prawo od elementu a_kk włącznie.

W przypadku tego rodzaju wyboru zmieniamy również kolejność kolumn w macierzy A. W takim przypadku zmienia się również kolejność zmiennych w wektorze x (trzeba te zmiany zapamiętywać w trakcie obliczeń).

7. Zadanie 1 - wygenerowanie przykładów do testowanie rozkładu Gaussa:

- stworzenie pewnej macierzy A oraz wektora x i wygenerowanie za pomocą odpowiedniej procedury mnożenia - wektora b.

8. Zadanie 2 - użycie wygenerowanych przykładów do rozwiązania układu równań (zastosowanie wyboru częściowego i rozwiązania macierzy trójkątnej górnej).

---